logistic 回归
#TOC
一、构造hypothesis假设函数
Logistic Regression 可以看做是一个 线性回归(Linear Regression) 经过一个sigmod激活函数 的结果。
线性回归方程:$ \theta_0 + \theta_1x_1+ \theta_2x_2+…+ \theta_n*n_n = \theta^T * x$
sigmoid函数:g(z)=11+e−z g(z) = \frac{1}{1+e^{-z}}g(z)=1+e−z1
所以hypothesis 函数 hθ(x)=11+e−θTxh_\theta (x) = \frac {1}{1+e^{-\theta^Tx}}hθ(x)=1+e−θTx1
hθ(x)h_\theta (x)hθ(x)表示为样本预测正例的概率
即:
KaTeX parse error: No such environment: equation at position 9:
\begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲
\left\{
\begin…
可以将公式(1)合并成:
(2)P(y∣x;θ)=hθ(x(i))y(i)(1−hθ(x(i)))1−y(i)P(y|x;\theta) = h_\theta(x^{(i)})^{y^{(i)}} (1-h_\theta(x^{(i)}))^{1- y^{(i)}} \tag{2}
P(y∣x;θ)=hθ(x(i))y(i)(1−hθ(x(i)))1−y(i)(2)
二、构造损失函数
下面介绍两种不同的构造假设函数的方法:
第一种是来源于NG的机器学习课程;
第二种是以概率的方式通过极大似然来构造代价函数
直接构造损失函数
构造代价函数:
KaTeX parse error: No such environment: equation at position 23: …heta) =
\begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲
\left\{
\begin…
[外链图片转存失败(img-NybE3yxJ-1565846168527)(media/15655785068654/15657637829206.jpg)]
如图一:
当y = 1,
若假设函数预测结果为1。 则代价函数为0;
当假设函数预测结果越接近0时,其代价就越大。
当 y = 0时同理
将两式化归一起:
Cost(θ)=−1m∑i=1my(i)loghθ(x)+(1−y(i))log1−hθ(x)Cost(\theta) = -\frac1m\sum_{i=1}^m y^{(i)}log^{h_\theta(x)} + (1-y^{(i)})log^{1 - h_\theta(x)}Cost(θ)=−m1i=1∑my(i)loghθ(x)+(1−y(i))log1−hθ(x)
使用概率知识,通过极大似然构造损失函数
优化的目标是是的P(y∣x;θ)P(y|x;\theta)P(y∣x;θ)的预测值最接近观测值。即使得:
∏i=1mP(yi∣x;θ)\prod_{i = 1}^m P(y_i|x;\theta)∏i=1mP(yi∣x;θ)的值取得最大。
构造似然函数:
L(θ)=∏i=1mP(y(i)∣x(i);θ)=∏i=1m(hθ(x))y(i)(1−hθ(x))1−y(i)L( \theta ) = \prod_{i = 1}^mP(y^{(i)}|x^{(i)};\theta) = \prod_{i = 1}^m(h_\theta(x))^{y^{(i)}}(1 - h_\theta(x) )^{1-y^{(i)}}L(θ)=i=1∏mP(y(i)∣x(i);θ)=i=1∏m(hθ(x))y(i)(1−hθ(x))1−y(i)
取对数:
l(θ)=∑i=1mlog((hθ(x))y(i)(1−hθy(i)(x))1−y(i))=∑i=1mlog(hθ(x))y(i)+log(1−hθ(x))1−y(i)=∑i=1my(i)loghθ(x)+(1−y(i))log1−hθ(x)l(\theta ) = \sum_{i = 1}^m log((h_\theta(x))^{y^{(i)}}(1 - h_\theta^{y^{(i)}}(x) )^{1-y^{(i)}}) \\
=\sum_{i = 1}^m log^{(h_\theta(x))^{y^{(i)}}} + log^{(1 - h_\theta(x) )^{1-y^{(i)}}} \\= \sum_{i=1}^m y^{(i)}log^{h_\theta(x)} + (1-y^{(i)})log^{1 - h_\theta(x)}l(θ)=i=1∑mlog((hθ(x))y(i)(1−hθy(i)(x))1−y(i))=i=1∑mlog(hθ(x))y(i)+log(1−hθ(x))1−y(i)=i=1∑my(i)loghθ(x)+(1−y(i))log1−hθ(x)
将求对数似然函数的极大值转变成求解代价函数的极小值:
令:J(θ)=−1ml(θ)J(\theta) = - \frac1ml(\theta)J(θ)=−m1l(θ)
损失函数最终形式:
J(θ)=−1m∑i=1my(i)loghθ(x)+(1−y(i))log1−hθ(x)
J(\theta) = -\frac1m\sum_{i=1}^m y^{(i)}log^{h_\theta(x)} + (1-y^{(i)})log^{1 - h_\theta(x)}
J(θ)=−m1i=1∑my(i)loghθ(x)+(1−y(i))log1−hθ(x)
三、损失函数优化(梯度下降)
sigmod 函数求导性质:
g′(z)=g(z)(1−g(z)) g'(z) = g(z)(1-g(z))g′(z)=g(z)(1−g(z))
Δθ=∂J(θ)∂θ=−1m∑i=1myhθ(x)hθ(x)(1−hθ(x))x+(1−yi)1−hθ(x)∗−1∗hθ(x)(1−hθ(x))x=−1m∑i=1my(1−hθ(x))x−(1−y)hθ(x)x=−1m∑i=1m(y(i)−hθ(x(i)))x(i)\Delta\theta = \frac{\partial J(\theta)}{\partial \theta} \\ = -\frac1m \sum_{i=1}^{m}\frac{y}{h_\theta(x)}h_\theta(x)(1-h_\theta(x))x+ \frac{(1-y_i)}{1-h_\theta(x)}*-1*h_\theta(x)(1-h_\theta(x))x \\ = -\frac1m \sum_{i=1}^{m}{y}(1-h_\theta(x))x - {(1-y)}h_\theta(x) x\\ = -\frac1m \sum_{i=1}^{m}(y^{(i)}-h_\theta(x^{(i)}))x^{(i)} Δθ=∂θ∂J(θ)=−m1i=1∑mhθ(x)yhθ(x)(1−hθ(x))x+1−hθ(x)(1−yi)∗−1∗hθ(x)(1−hθ(x))x=−m1i=1∑my(1−hθ(x))x−(1−y)hθ(x)x=−m1i=1∑m(y(i)−hθ(x(i)))x(i)
参数更新:
θj=θj−αΔθj=θj−α1m∑i=1m(hθ(x(i))−y(i))x(i)\theta_j = \theta_j - \alpha\Delta\theta_j = \theta_j - \alpha\frac1m \sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x^{(i)}θj=θj−αΔθj=θj−αm1i=1∑m(hθ(x(i))−y(i))x(i)
四、正则
L1 正则:
J(θ)=−1m∑i=1my(i)loghθ(x)+(1−y(i))log1−hθ(x)+λ∣∣θ∣∣J(\theta) = -\frac1m\sum_{i=1}^m y^{(i)}log^{h_\theta(x)} + (1-y^{(i)})log^{1 - h_\theta(x)} + \lambda||\theta||J(θ)=−m1i=1∑my(i)loghθ(x)+(1−y(i))log1−hθ(x)+λ∣∣θ∣∣
L2 正则:
J(θ)=−1m∑i=1my(i)loghθ(x)+(1−y(i))log1−hθ(x)+λ∣∣∣θ∣∣2J(\theta) = -\frac1m\sum_{i=1}^m y^{(i)}log^{h_\theta(x)} + (1-y^{(i)})log^{1 - h_\theta(x)} + \lambda|||\theta ||^2J(θ)=−m1i=1∑my(i)loghθ(x)+(1−y(i))log1−hθ(x)+λ∣∣∣θ∣∣2
五、logistic Regression 为什么要使用 sigmod 函数
指数分布族概念:可以表示为指数形式的概率分布。
fX(x∣θ)=h(x)exp(η(θ)∗T(x)−A(θ))f_X(x|\theta) = h(x)exp(\eta(\theta)*T(x) - A(\theta))fX(x∣θ)=h(x)exp(η(θ)∗T(x)−A(θ))
将伯努利分布化成指数分布族的形式:
KaTeX parse error: No such environment: equation at position 9:
\begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲
\begin{split}
…
因此可以得出:
η=logϕ1−ϕ \eta = log{\frac{\phi}{1-\phi}}η=log1−ϕϕ
可以化简出:
ϕ=11+e−η\phi = \frac1{1+e^{-\eta}}ϕ=1+e−η1
logistic 模型的前置概率估计是伯努利分布
为什么不用均方差值作为损失函数吗?
因为使用均方差作为损失函数是非凸函数。





 本文详细介绍了逻辑回归的原理,包括构造hypothesis假设函数、损失函数(直接构造与极大似然构造)、梯度下降优化过程以及正则化。重点探讨了为何选择sigmoid函数,并解释了为何不使用均方差作为损失函数的原因。
本文详细介绍了逻辑回归的原理,包括构造hypothesis假设函数、损失函数(直接构造与极大似然构造)、梯度下降优化过程以及正则化。重点探讨了为何选择sigmoid函数,并解释了为何不使用均方差作为损失函数的原因。

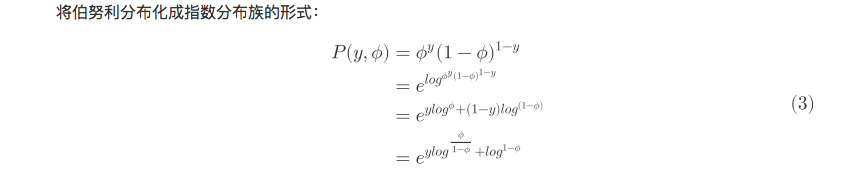
















 542
542

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








