方程组求解-高斯消元法

最新推荐文章于 2025-01-06 06:30:00 发布

原创

最新推荐文章于 2025-01-06 06:30:00 发布 · 1.1k 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#线性代数 #算法 #lua #矩阵

本文介绍了如何使用高斯消元法解决线性方程组，详细阐述了基本思路和具体步骤，并提供了一个lua语言的代码实现，通过构建上三角矩阵并回代求解，最终得出解向量。

问题描述：

对如下方程组利用高斯消元法求解x1~xn

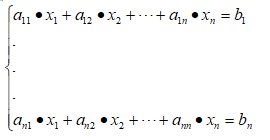
基本思路：

通过行列变化将方程组转化为上三角矩阵，再逐一回代求解出解向量。

具体步骤：

1.构建上三角矩阵

k从1到n迭代:

第一步：以k行k列为起点的矩阵中最大的系数通过行列交换到k行k列

第二步：将第k行/akk使得xk的系数变成1

第三步：将第k行按系数加到K+1至n行使得k+1至n行xk的系数0

2.回代求解

第一步：从第n行开始回代消元，求出x1~xn

第二部：依据之前的列交换将x1~xn正确排序

代码实现（lua）：

下面是一个lua版本的实现，其中matrix为系数矩阵，bVector为解向量，n为阶数。

最终有解返回true，否则返回false

最终的x1~xn储存在bVector中

---@param matrix table 方程组矩阵
---@param n number 方程组阶数
---对每一行：
---1.主元素下方矩阵中最大的系数交换到主元素(行交换和列交换)
---2.主元素系数置为1
---3.将剩余行对应主元素列的系数置为0
---4.回代求解
function _M:ResolveMatrix_Gauss(matrix, bVector, n)
    local maxVal = 0 --记录的最大值
    local is = 0 --行交换记录
    loc