51NOD2000 - 四边形分割平面(使用矩阵求通项公式)

最新推荐文章于 2022-09-14 18:18:28 发布

原创最新推荐文章于 2022-09-14 18:18:28 发布 · 670 阅读

0 ·

CC 4.0 BY-SA版权

OJ 同时被 2 个专栏收录

138 篇文章

订阅专栏

算法

40 篇文章

订阅专栏

本文详细解析了一种通过叠加正方形来最大化分隔区域数量的问题，并给出了两种解决方案：一种是使用递推公式进行预计算，另一种是通过数学推导得出直接公式。同时，还介绍了如何运用矩阵快速幂的方法求解该问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

这道题挺有意思的，和HDU5047 - Sawtooth[找规律]的类型是一样的，关键问题在于你要知道如何分割使得区域个数最多以及求出递推公式或直接公式。

题目链接：点这儿。

我们先来看一张图，看看如何叠加正方形使得分隔的区域数最多。
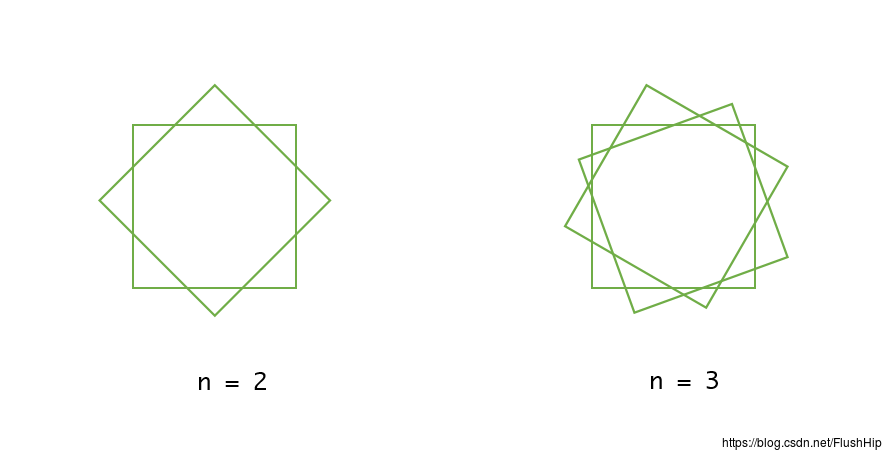
这里写图片描述

这么叠加会生成最多的分隔区域，具体分析可以参考HDU5047 - Sawtooth[找规律]。

因此可以得到递推式： $F_n = F_{n-1}+8(n-1)$ 。

由于这个题的数据量不大，因此可以打表输出就行。

#include <bits/stdc++.h>

using namespace std;

const int maxn = 10001;

int f[maxn];

void init()
{
    f[1] = 2;
    for (int i = 2; i < maxn; ++i)
        f[i] = f[i - 1] + 8 * (i - 1);
}

int main()
{
    init();
    int T;
    scanf("%d", &T);
    for (int n; T--; ) {
        scanf("%d", &n);
        printf("%d\n", f[n]);
    }
    return 0;
}

或者利用迭代(同样参见HDU5047 - Sawtooth[找规律])求出最终公式： $F_n=2 + 4n(n-1)$ 。

其实我一开始没有想到迭代这一做法，我的最直接想法竟然是矩阵快速幂，因此这里我把我一开始的做法分享一下。

这个公式 $F_n=2 + 4n(n-1)$ 可以得到一个矩阵等式

⎡ ⎣ ⎢ 100110081 ⎤ ⎦ ⎥ n - 1 \times ⎡ ⎣ ⎢ F 1 81 ⎤ ⎦ ⎥ = ⎡ ⎣ ⎢ 100110081 ⎤ ⎦ ⎥ \times ⎡ ⎣ ⎢ F n - 1 8 (n - 1) 1 ⎤ ⎦ ⎥ = ⎡ ⎣ ⎢ F n 8 n 1 ⎤ ⎦ ⎥

$\begin{equation*} \begin{bmatrix} 1&1&0\\ 0 & 1&8\\ 0 & 0&1\\ \end{bmatrix}^{n-1}\times \begin{bmatrix} F_{1}\\ 8\\ 1\\ \end{bmatrix}= \begin{bmatrix} 1&1&0\\ 0 & 1&8\\ 0 & 0&1\\ \end{bmatrix}\times \begin{bmatrix} F_{n - 1}\\ 8(n-1)\\ 1\\ \end{bmatrix}= \begin{bmatrix} F_{n}\\ 8n\\ 1\\ \end{bmatrix} \end{equation*}$

具体详情可以参加博文深入浅出矩阵快速幂及其简单应用。

现在的问题就变成了

⎡ ⎣ ⎢ 100110081 ⎤ ⎦ ⎥ n - 1 = ?

$\begin{equation*} \begin{bmatrix} 1&1&0\\ 0 & 1&8\\ 0 & 0&1\\ \end{bmatrix}^{n-1}=? \end{equation*}$

令

A = ⎡ ⎣ ⎢ 100110081 ⎤ ⎦ ⎥, B = ⎡ ⎣ ⎢ 000100080 ⎤ ⎦ ⎥

$\begin{equation*} A=\begin{bmatrix} 1&1&0\\ 0 & 1&8\\ 0 & 0&1\\ \end{bmatrix}, B=\begin{bmatrix} 0&1&0\\ 0 & 0&8\\ 0 & 0&0\\ \end{bmatrix} \end{equation*}$

则

A = E + B ， B 2 = ⎡ ⎣ ⎢ 000000800 ⎤ ⎦ ⎥, B 3 = B 4 = \dots = B n = ⎡ ⎣ ⎢ 000000000 ⎤ ⎦ ⎥

$\begin{equation*} A = E+B， B^2=\begin{bmatrix} 0&0&8\\ 0 & 0&0\\ 0 & 0&0\\ \end{bmatrix}, B^3=B^4=\cdots=B^n=\begin{bmatrix} 0&0&0\\ 0 & 0&0\\ 0 & 0&0\\ \end{bmatrix} \end{equation*}$

所以

A n - 1 = (E + B) n - 1 = E n - 1 + (n - 1) E n - 2 B + ( n - 1 ) ( n - 2 ) 2 B 2 = ⎡ ⎣ ⎢ 100 n - 1 10 4 (n - 1) (n - 2) 8 (n - 1) 1 ⎤ ⎦ ⎥

$\begin{equation*} A^{n-1} = (E+B)^{n-1}=E^{n-1}+(n-1)E^{n-2}B+\frac{(n-1)(n-2)}{2}B^2\\ =\begin{bmatrix} 1&n-1&4(n-1)(n-2)\\ 0 & 1&8(n-1)\\ 0 & 0&1\\ \end{bmatrix} \end{equation*}$

即 $F_n=F_1*1+8*(n-1)+4(n-1)(n-2)*1=2 + 4n(n-1)$ 。

我一开始就是这么做的！也好，给自己开阔了一个新的求通项公式的路子，也复习了线性代数。

#include <bits/stdc++.h>

using namespace std;

int main()
{
    int T;
    scanf("%d", &T);
    for (int n; T--; ) {
        scanf("%d", &n);
        printf("%d\n", 2 + 4 * n * (n - 1));
    }
    return 0;
}