排序算法总结（下）

八、计数排序（Counting Sort）

计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。
作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。
1.算法简介
计数排序(Counting sort)是一种稳定的排序算法。计数排序使用一个额外的数组C，其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。它只能对整数进行排序。
2.算法描述和实现
具体算法描述如下：
（1） 找出待排序的数组中最大和最小的元素；
（2） 统计数组中每个值为i的元素出现的次数，存入数组C的第i项；
（3）对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；
（4） 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。

代码实现如8.1

计数排序动态图演示过程如下图所示：

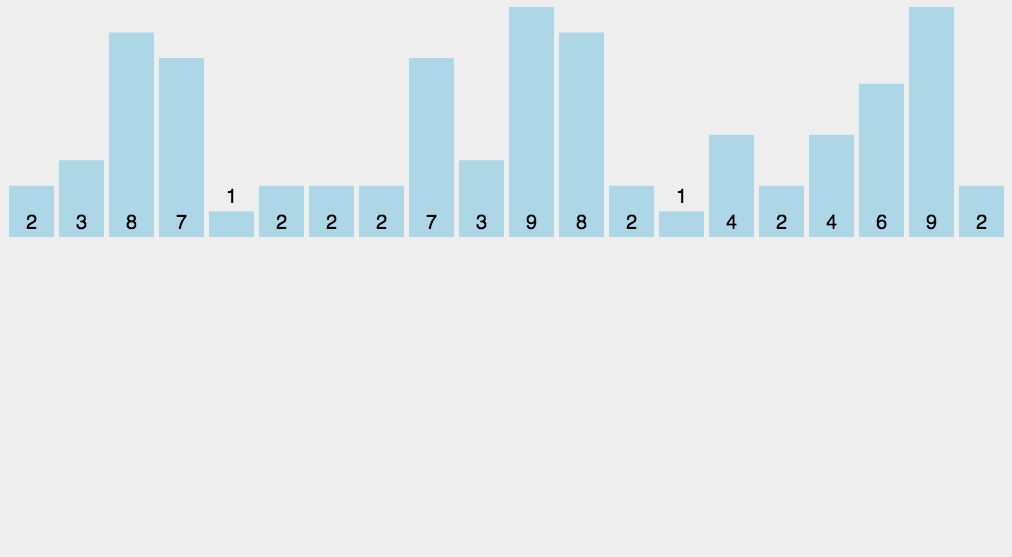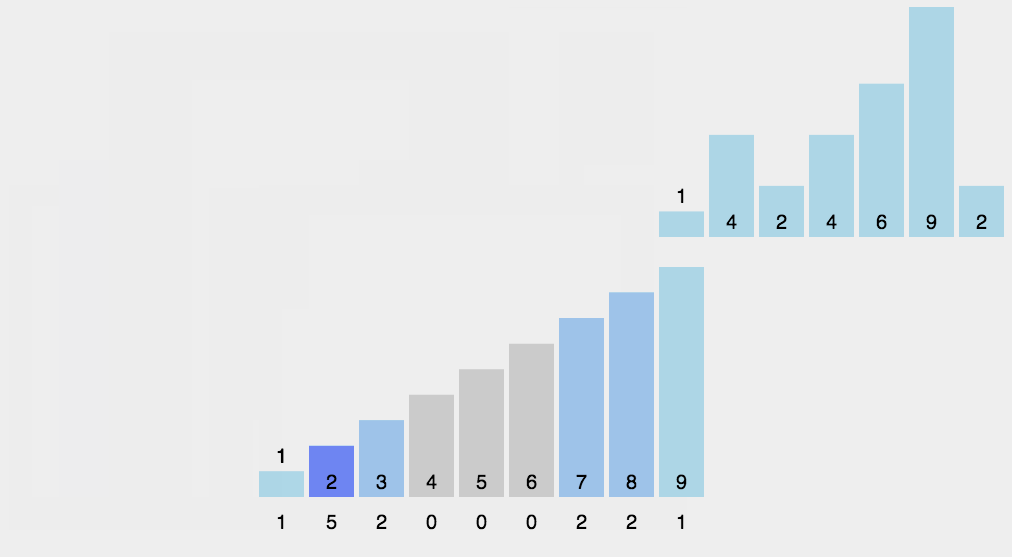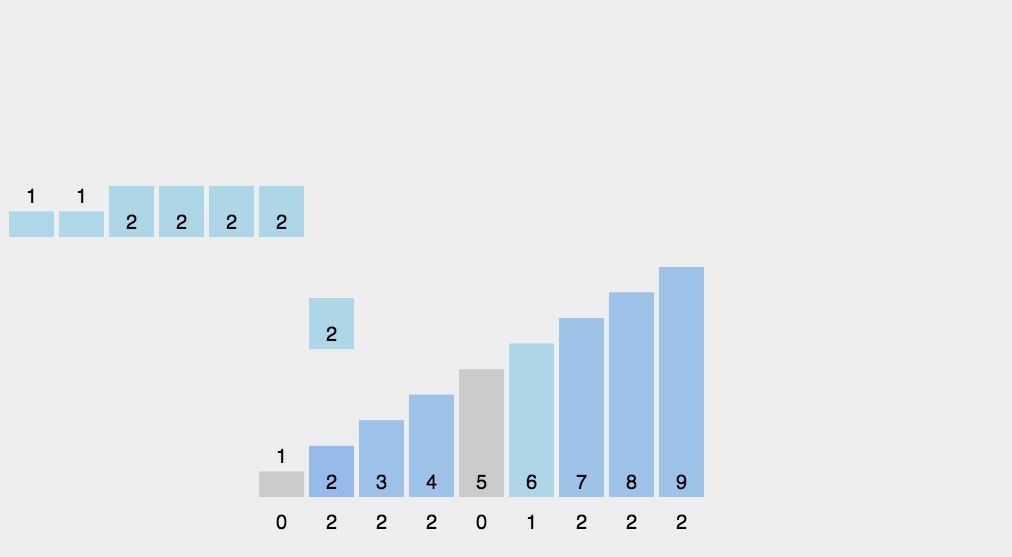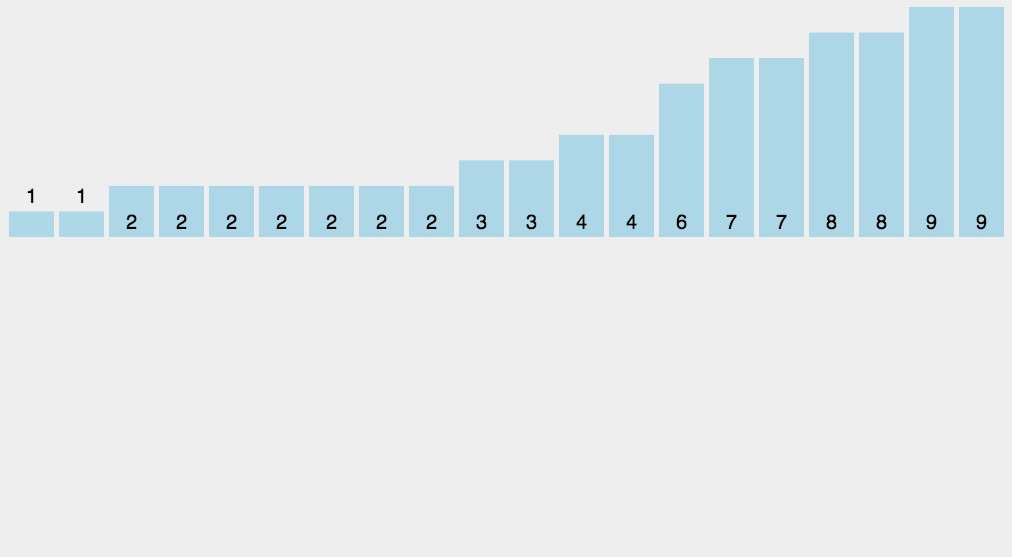
3.算法分析

特点
当输入的元素是n 个0到k之间的整数时，它的运行时间是 O(n + k)。计数排序不是比较排序，排序的速度快于任何比较排序算法。由于用来计数的数组C的长度取决于待排序数组中数据的范围（等于待排序数组的最大值与最小值的差加上1），这使得计数排序对于数据范围很大的数组，需要大量时间和内存

情况	时间复杂度	数据
最佳情况	T(n) = O(n+k)	-
最差情况	T(n) = O(n+k)	-
平均情况	T(n) = O(n+k)	-

4.优化

九、桶排序（Bucket Sort）

桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。
1.算法简介
桶排序 (Bucket sort)的工作的原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排
2.算法描述和实现
具体算法描述如下：
（1）设置一个定量的数组当作空桶；
（2）遍历输入数据，并且把数据一个一个放到对应的桶里去；
（3）对每个不是空的桶进行排序；
（4）从不是空的桶里把排好序的数据拼接起来。

代码实现如9.1

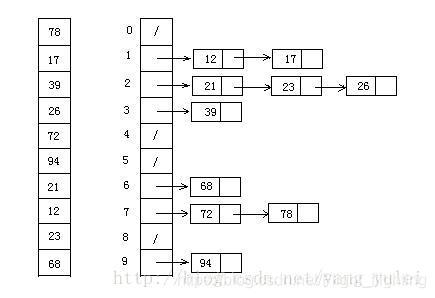
桶排序过程如下图所示：

3.算法分析

特点
桶排序最好情况下使用线性时间O(n)，桶排序的时间复杂度，取决与对各个桶之间数据进行排序的时间复杂度，因为其它部分的时间复杂度都为O(n)。很显然，桶划分的越小，各个桶之间的数据越少，排序所用的时间也会越少。但相应的空间消耗就会增大

情况	时间复杂度	数据
最佳情况	T(n) = O(n+k)	-
最差情况	T(n) = O(n+k)	-
平均情况	T(n) = O(n^2)	-

4.优化

十、基数排序（Radix Sort）

基数排序也是非比较的排序算法，对每一位进行排序，从最低位开始排序，复杂度为O(kn),为数组长度，k为数组中的数的最大的位数；
1.算法简介
基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。基数排序基于分别排序，分别收集，所以是稳定的。
2.算法描述和实现
具体算法描述如下：
（1）取得数组中的最大数，并取得位数；
（2）arr为原始数组，从最低位开始取每个位组成radix数组；
（3）对radix进行计数排序（利用计数排序适用于小范围数的特点）；

代码实现如10.1

基数排序LSD动态图演示过程如下图所示：

3.算法分析

情况	时间复杂度	数据
最佳情况	T(n) = O(n*k)	-
最差情况	T(n) = O(n*k)	-
平均情况	T(n) = O(n*k)	-

基数排序有两种方法：

基数排序种类	特点
MSD	从高位开始进行排序
LSD	从低位开始进行排序

基数排序 vs 计数排序 vs 桶排序
这三种排序算法都利用了桶的概念，但对桶的使用方法上有明显差异：

排序方法	特点
基数排序	根据键值的每位数字来分配桶
计数排序	每个桶只存储单一键值
桶排序	每个桶存储一定范围的数值

4.优化

引用排序算法总结