Trees

最新推荐文章于 2025-08-22 13:30:00 发布

原创最新推荐文章于 2025-08-22 13:30:00 发布 · 310 阅读

0 ·

CC 4.0 BY-SA版权

数据结构与算法专栏收录该内容

14 篇文章

订阅专栏

Trees

基本概念

特点：
（1）每个结点有零个或多个子节点
（2）每个结点只有一个父节点
（3）没有前驱的结点为根节点
（4）除了根节点外，每个子节点可分为m个不相交的子树
概念
（1）结点的度：一个结点含有子树的个数
（2）树的度：最大的结点的度
（3）叶结点：度为零的结点
（4）分支结点：度不为零的结点
（5）孩子结点：一个结点子树的根节点
（6）双亲结点：含有孩子的结点（或称为父结点）
（7）兄弟结点：具有相同双亲结点
（8）祖先结点：从根到该结点所经分支上的所有结点
（9）子孙结点：以某结点为根的子树中任意结点
（10）结点的层次：
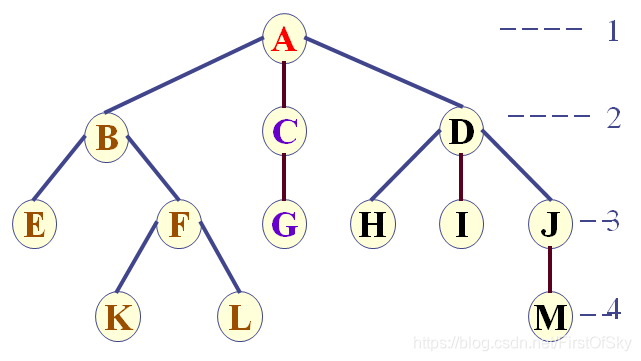
在这里插入图片描述

（11）树的高度或深度：树中结点的最大层次
（12）路径：从根结点到某一结点的一条通路
（13）路径长度：路径经过的边数
（14）有序树VS无序树：任意结点的子结点是否有顺序关系

基本操作——遍历

1.前序遍历
（1）访问根结点
（2）按照从左到右的顺序遍历根结点的每一棵子树。

2.后序遍历
（1）按照从左到右的顺序遍历根结点的每一棵子树。
（2）访问根结点

3.层序遍历
从第一层开始，从上到下逐层遍历，同层按从左到右的顺序遍历
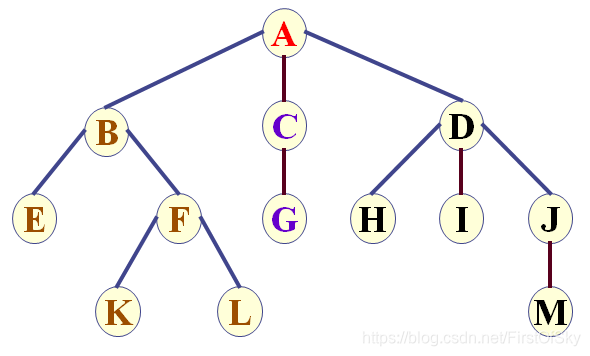
在这里插入图片描述
前序：ABEFKLCGDHIJM
后序：EKLFBGCHIMJDA
层序：ABCDEFGHIJKLM

存储结构

1、双亲表示法

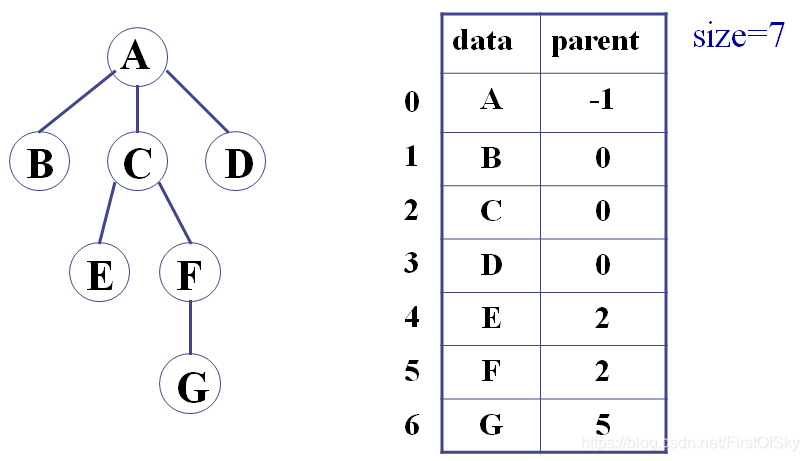
在这里插入图片描述

#define MaxSize 100 
template <class T>
struct pNode
{
 T data;
 int parent;
};
template <class T>
pNode<T>  Tree[MaxSize];
int size;

改进：带右兄弟的双亲表示法
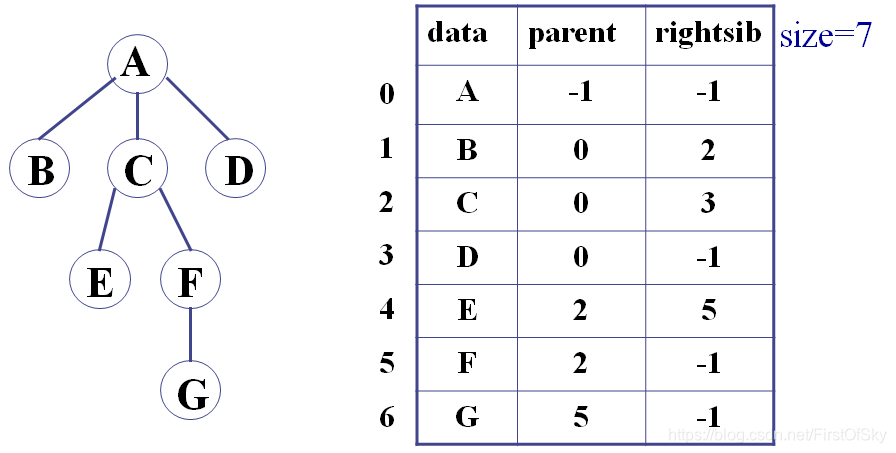
在这里插入图片描述

#define MaxSize 100 
template <class T>
struct pNode
{
 T data;
 int parent;
};
template <class T>
pNode<T>  Tree[MaxSize];
int size;

2、孩子表示法

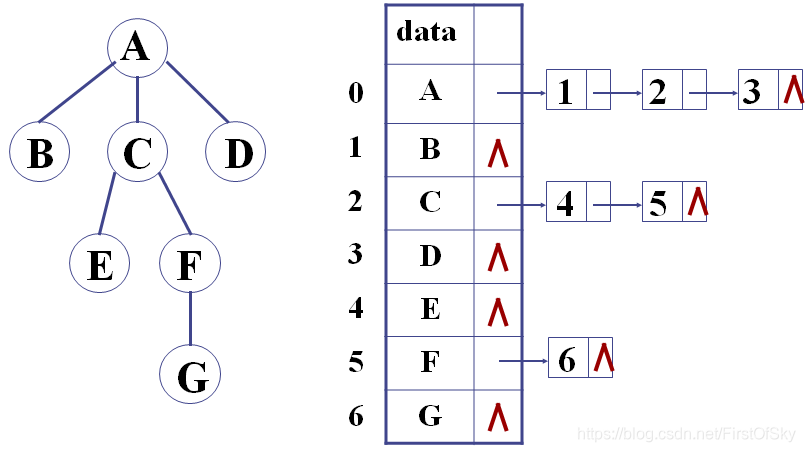
在这里插入图片描述

struct CNode
{
 int  child;
 CNode *next;
};
template <class T>
struct CBNode
{
 T  data;
 CNode  *firstchild;
};

改进：双亲孩子表示法：
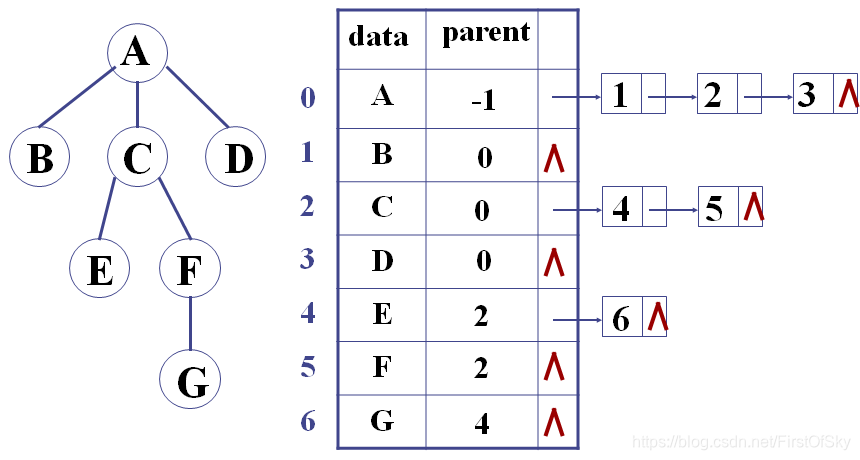
在这里插入图片描述

3、多重链表法

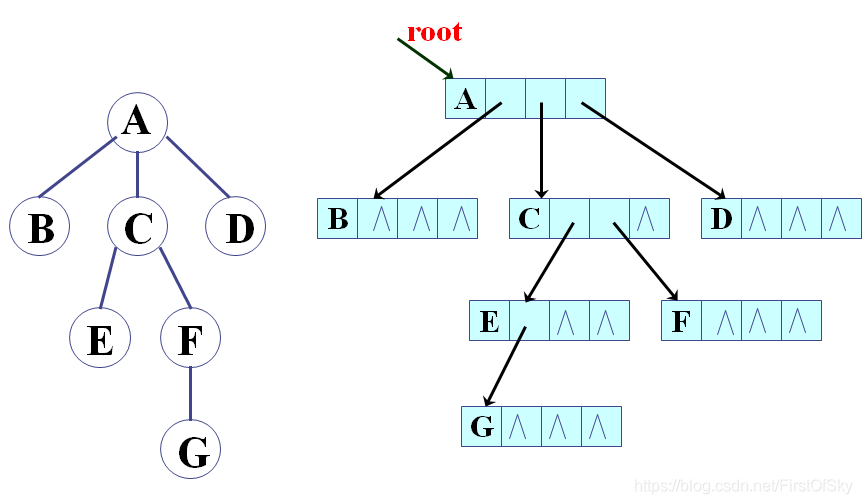
在这里插入图片描述
缺点：浪费大量指针

4、孩子兄弟表示法

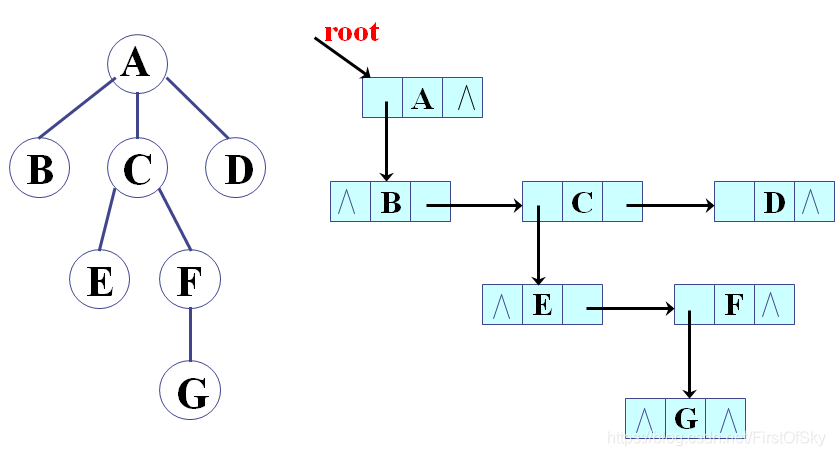
在这里插入图片描述

template <class T>
struct TNode
{
 T data;
 TNode<T>  *firstchild, *rightsib;
};

下一篇二叉树