人理解迭代，而神理解递归————递归思想心得

        一、递归（Recursion），顾名思义，有递去有归来。在编程中，最常见的就是总问题与其子问题的思路完全一致，即解决了该子问题，总问题也就迎刃而解。

        有人会问，递归与循环有什么区别呢？递归也是把子问题一个一个的解决，总问题也就解决了，与循环思想差不多啊？通俗点讲：

        递归：你打开面前这扇门，看到屋里面还有一扇门。你走过去，发现手中的钥匙还可以打开它，你推开门，发现里面还有一扇门，你继续打开它。若干次之后，你打开面前的门后，发现只有一间屋子，没有门了。然后，你开始原路返回，每走回一间屋子，你数一次，走到入口的时候，你可以回答出你到底用这你把钥匙打开了几扇门。

　　 循环：你打开面前这扇门，看到屋里面还有一扇门。你走过去，发现手中的钥匙还可以打开它，你推开门，发现里面还有一扇门（若前面两扇门都一样，那么这扇门和前两扇门也一样；如果第二扇门比第一扇门小，那么这扇门也比第二扇门小，你继续打开这扇门，一直这样继续下去直到打开所有的门。但是，入口处的人始终等不到你回去告诉他答案。

        好了，说回之前的“有递去有归来”的思想。

        递去：将总问题从前向后，一个一个分解为相同的子问题。

        归来：遇到终止条件后（终止条件必须明确，否则会出现无限递归，锁死），开始将子问题一个一个按倒序解决。

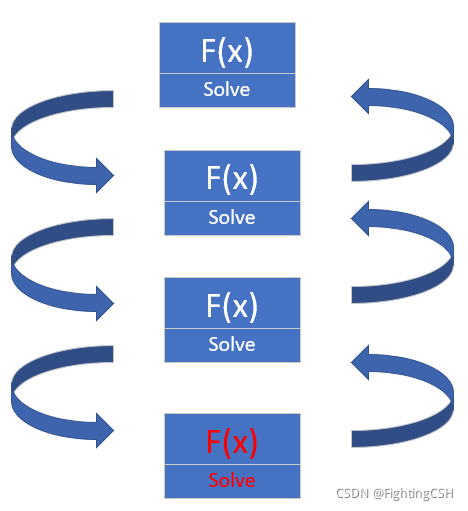
由于总问题与子问题的解决方法完全一致，所以会出现函数调用自身的情况。

        二、我们在初中都学过“数学归纳法”。用“数学归纳法”的思想去理解递归也不错：

数学归纳法：
1.i = 0，i = 1时，结论成立
2.若i = n时，结论仍旧成立，则i = n+1时,结论亦成立

数学归纳法是正确的递归思考方式，第 1 点称为基本情况，第 2 点称为通用情况。

数学归纳法适用于将解决的原问题转化为解决它的子问题，而它的子问题又变成子问题的子问题，而且我们发现这些问题其实都是一个模型，也就是说存在相同的逻辑归纳处理项。当然有一个是例外的，也就是归纳结束的那一个处理方法不适用于我们的归纳处理项，当然也不能适用，否则我们就无穷归纳了。

总的来说，归纳法主要包含以下三个关键要素：

1）步进表达式：问题蜕变成子问题的表达式 
2）结束条件：什么时候可以不再使用步进表达式 
3）直接求解表达式：在结束条件下能够直接计算返回值的表达式 
事实上，这也正是某些数学中的数列问题在利用编程的方式去解决时可以使用递归的原因，比如著名的斐波那契数列问题。

        三、递归的三要素

　　 在我们了解了递归的基本思想及其数学模型之后，我们如何才能写出一个漂亮的递归程序呢？笔者认为主要是把握好如下三个方面：

1、明确递归终止条件；

2、给出递归终止时的处理办法；

3、提取重复的逻辑，缩小问题规模。

1). 明确递归终止条件

　　 我们知道，递归就是有去有回，既然这样，那么必然应该有一个明确的临界点，程序一旦到达了这个临界点，就不用继续往下递去而是开始实实在在的归来。换句话说，该临界点就是一种简单情境，可以防止无限递归。

2). 给出递归终止时的处理办法

　　 我们刚刚说到，在递归的临界点存在一种简单情境，在这种简单情境下，我们应该直接给出问题的解决方案。一般地，在这种情境下，问题的解决方案是直观的、容易的。

3). 提取重复的逻辑，缩小问题规模*

　　 我们在阐述递归思想内涵时谈到，递归问题必须可以分解为若干个规模较小、与原问题形式相同的子问题，这些子问题可以用相同的解题思路来解决。从程序实现的角度而言，我们需要抽象出一个干净利落的重复的逻辑，以便使用相同的方式解决子问题

        四、建立编程模型

模型一：递去过程中解决问题

function recursion(大规模){
    if (end_condition){      // 明确的递归终止条件
        end;   // 简单情景
    }else{            // 在将问题转换为子问题的每一步，解决该步中剩余部分的问题
        solve;                // 递去
        recursion(小规模);     // 递到最深处后，不断地归来
    }
}

模型二：归来过程中解决问题

function recursion(大规模){
    if (end_condition){      // 明确的递归终止条件
        end;   // 简单情景
    }else{            // 先将问题全部描述展开，再由尽头“返回”依次解决每步中剩余部分的问题
        recursion(小规模);     // 递去
        solve;                // 归来
    }
}

本文有参考下面文章的思路，笔者也是根据下面的文章学习的递归思想

递归算法的讲解_jacklin_01的博客-优快云博客_递归详解

例题请看：Leetcode刷题心得（No.24：两两交换链表中的结点）（三指针，递归）_FightingCSH的博客-优快云博客