图论-拓扑排序(有向图)

拓扑排序的两种求法：

First:利用discoverTime(发现时间)&finishTime(结束时间)
Second:利用入度

第一种:



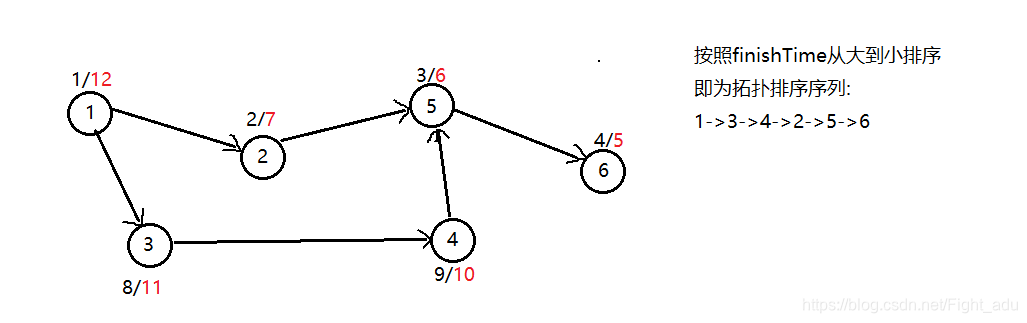
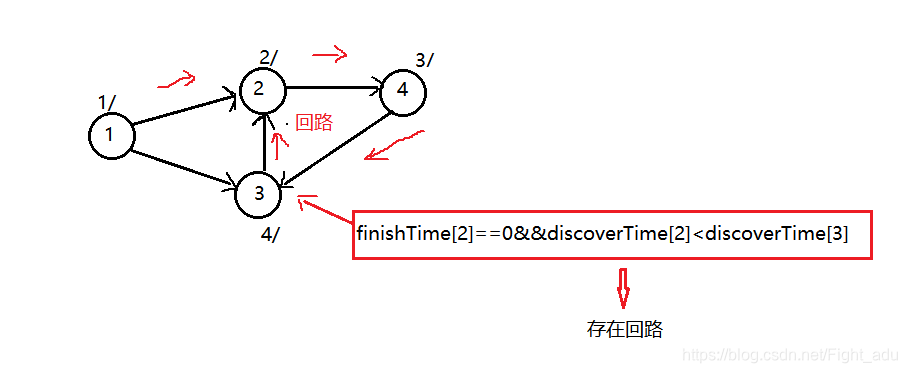
Code:

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int ans=1,flagCycle=0;//开始时间初值 标志位-是否存在回路 
vector<int>tp;//拓扑系列 
vector<vector<int>>g;//邻接表 
vector<bool>visit;//是否被访问过 
vector<int>discoverTime,finishTime;//发现时间 结束时间 
int N,M;
void dfs(int x){
	discoverTime[x]=ans++;//记录发现时间 
	visit[x]=true;
	for(int i=0;i<g[x].size();i++){//找X的邻接点 
		if(discoverTime[g[x][i]]==0)//判断这个点是否访问过 没被访问则进行访问 
			dfs(g[x][i]);
		//如果g[x][i]节点的finishTime为0说明还有邻接点未被访问到
		//discoverTime[x]<discoverTime[g[x][i]]说明x节点又访问它前面的节点 
		//没有回路的图是不会在此节点未访问完前 去访问其祖先的节点 
		else if(finishTime[g[x][i]]==0&&discoverTime[g[x][i]]<discoverTime[x]){//判断是否存在回路 
			flagCycle=1;
			return;
		}
	}
	tp.push_back(x);//记录下拓扑排序序列  
	finishTime[x]=ans++;
}
int main(){
	cin>>N>>M;
	//节点下标从1开始 
	g.resize(N+1);
	visit.resize(N+1);
	discoverTime.resize(N+1);
	finishTime.resize(N+1);
	for(int i=0;i<M;i++){
		int a,b;
		cin>>a>>b;
		g[a].push_back(b);
	}
	for(int i=1;i<=N;i++) 
		if(!visit[i])
			dfs(i);
	if(flagCycle)//判断flagCycle是否为1  
		cout<<"存在回路";
	else{
		cout<<"拓扑排序为:"<<endl;
	for(int i=tp.size()-1;i>=0;i--)
		cout<<"id:"<<tp[i]<<" "<<"discoverTime: "<<discoverTime[tp[i]]<<" "<<"FinishTime: "<<finishTime[tp[i]]<<endl;
	} 
	return 0;
}

第二种:



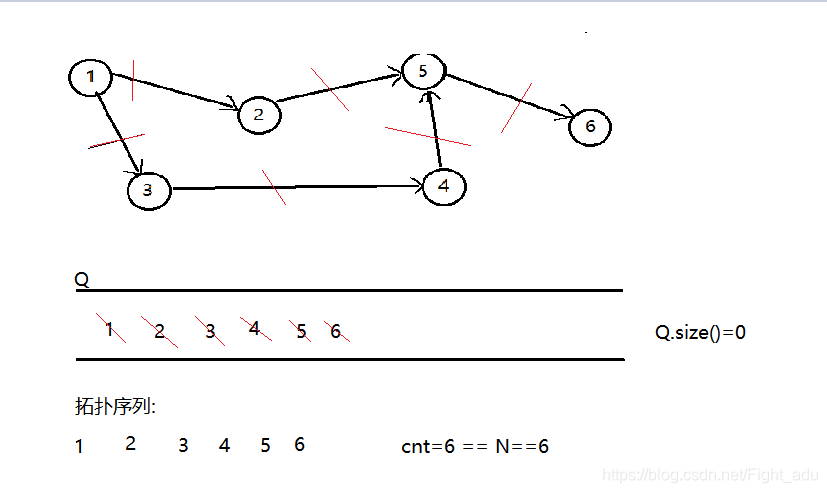
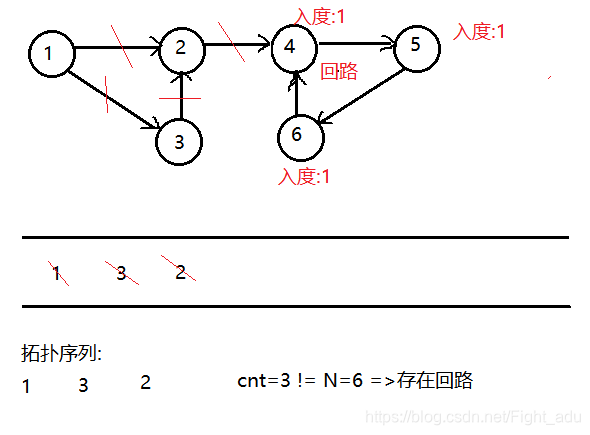
Code:

#include<iostream>
#include<vector>
#include<queue>
#include<algorithm>
#include<numeric>
using namespace std;
vector<vector<int>>g;
vector<int>numEdg;
vector<int>Path;
queue<int>Enq;
int N,M;
int flagCycle=0,cnt=1;
void TopSort(){
	int v; 
	for(int i=1;i<=N;i++)//查找是否存在入度为0的节点 
		if(numEdg[i]==0)
			Enq.push(i);//把入度为0的结点放入队列里 
		while(!Enq.empty()){//判断队列是否为空  
			v=Enq.front();//取对头元素 
			Path.push_back(v);//把它加入拓扑排序队列中 
			Enq.pop();//从队列中删除 =>从图中抹掉这个节点  
			for(int i=0;i<g[v].size();i++)//遍历这个节点它的所有邻接 把它们的入度-1 
				if(--numEdg[g[v][i]]==0){//入度减一之后节点是否为0  若为0则是拓扑排序序列中元素 
					cnt++;//拓扑排序个数+1 
					Enq.push(g[v][i]);//将入度为0的元素放入队列中 
			}
		}
		if(cnt!=N)//拓扑序列中的个数是否和元素个数相等  不相等说明有回路 
			flagCycle=1;
}
int main(){
	cin>>N>>M;
	g.resize(N+1);//邻接表 
	numEdg.resize(N+1);//用来存储各个节点的入度	
	for(int i=0;i<M;i++){
		int a,b,c;
		cin>>a>>b;
		g[a].push_back(b);
		numEdg[b]++;//统计入度个数 
	}
	TopSort();
	if(flagCycle)//进行判断是否存在回路 
		cout<<"存在回路";
	else{
		cout<<"拓扑排序序列为:"<<endl;
		for(int i=0;i<Path.size();i++)
			cout<<Path[i]<<" ";
	}
	
}