小白学习之机器学习

机器学习：使机器自己学习如何去做有趣的事情

一、机器学习主要分为两种类型：监督学习（supervised learning）与无监督学习(unsupervised

learning)

监督学习（supervised learning）：回归与分类

回归：预测连续值输出

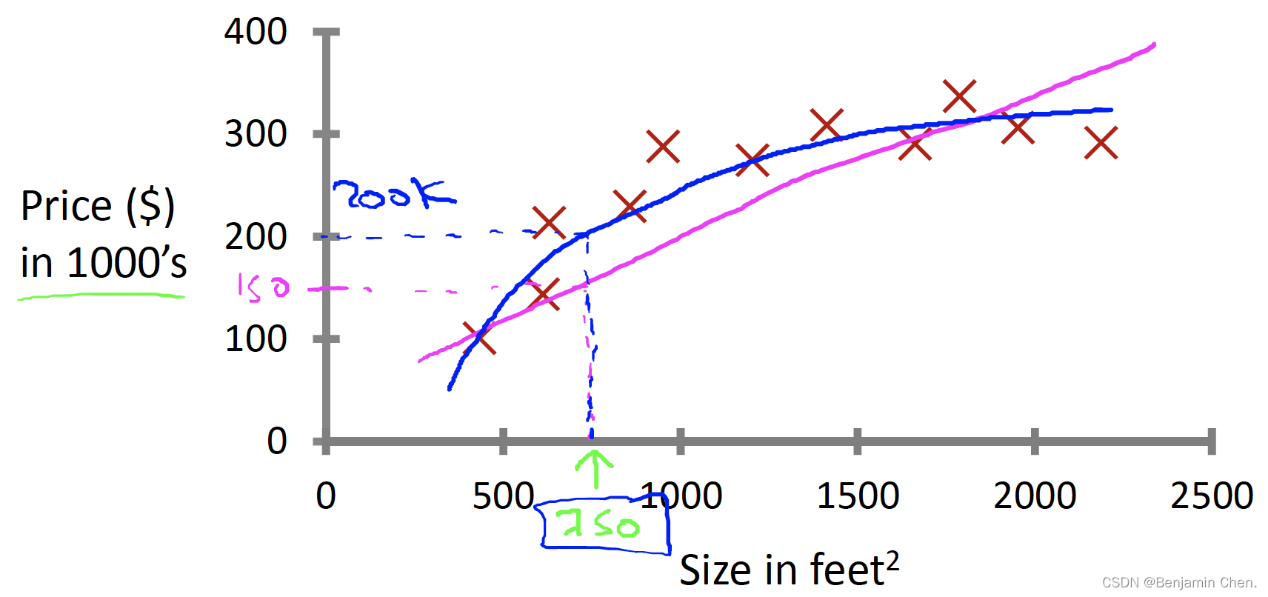
已知一个数据集，已知房子的平方英尺数，预测房子的价格。可以通过一条直线拟合数据，或者通过二次函数拟合数据。如何选择和如何决定用什么拟合数据会有更好的结果。

Supervised Learning“right answers” given →数据集包含正确答案，算法基于正确答案预测更多的正确答案

分类：预测一个离散值输出

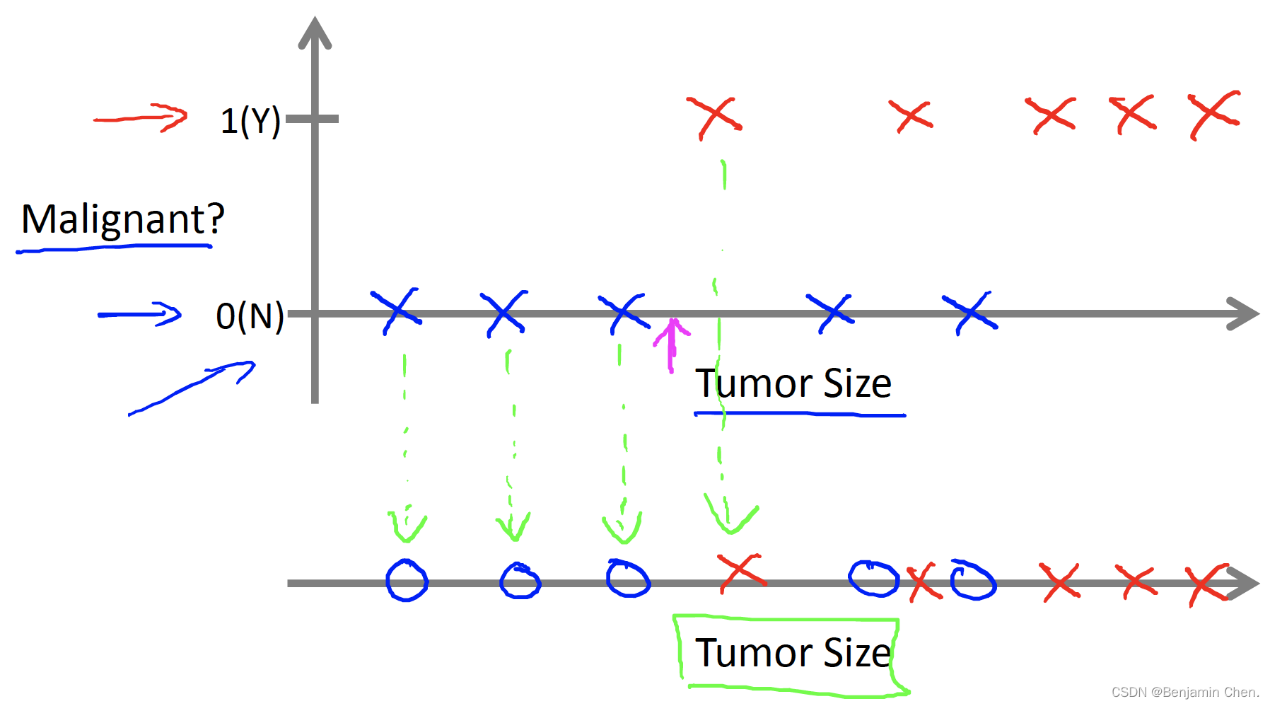
已知一个数据集，已知肿瘤的大小，预测肿瘤是良性还是恶性的概率

无监督学习(unsupervised learning)

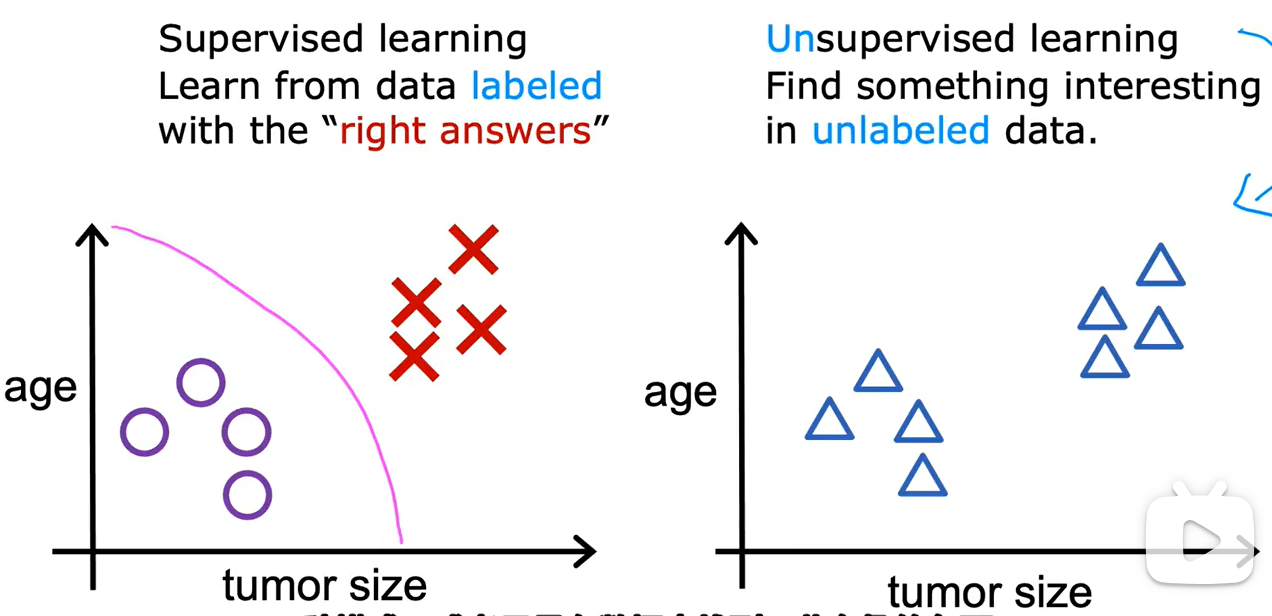
1. 非监督学习没有任何labels标签
2. 非监督学习会把数据分成不同的clusters簇
3. 非监督学习是clustering algorithm聚类算法

应用：如谷歌算法

数据中只有输入值x，没有输出值y，算法必须从数据中找出规律

数据中只有输入值x，没有输出值y，算法必须从数据中找出规律

二、线性回归模型（Linea Regression Mondel）拟合为一条直线

predict number

分类模型（classification model）

predict categoies and discrete catagoies

监督学习工作

training set ( features and prediction)

接着

learning algorithm

里面有fanction f

由 input x  通过faction f  得到 estimate and prediction (即y尖)

m = Number of training examples →训练样本的数量

x= “input” variable / features 输入变量 / 特征

y = “output” variable / “target” variable 输出变量 / 目标变量

(x, y) = single training example 一个训练样本

(x(i), y(i)) = ith training example 第i个训练样本

三、单变量线性回归（Univariate linear regression）

f(x)=wx+b

w 与b 为模型的参数（paramenters）

可以被称为系数（coefficients）或权重(weights)

四、成本函数（cost function）tell us how well the model is doing

平方误差成本函数（the squared error cost function）

 

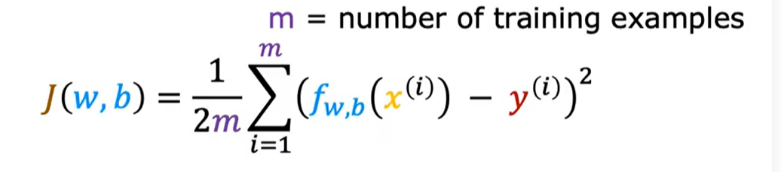
利用成本函数为模型找到最佳参数（不断变化w和b的值，同时计算J(w,b)的值，直到找到J(w,b）的最小值，即为最佳参数)

五、梯度下降（gradient decent）:it could use to try to minimize any function

理解：此时站在山峰上的最高点，找最近的哪低到哪，如此循环直到找到局部最低点。

1.阿尔法是学习率，指的是控制梯度下降到步子，越大其梯度下降的越迅速

2.同时更新w 和b

左侧为正确，右侧为错误，实现同步更新，右侧是把tmp_w算出来，立刻赋值变量给w，这样无法实现w,b的同时更新。

3.学习率如果α太小，需要很多步才能到达最低点，梯度下降速度变慢

如果α太大，梯度下降可能会越过最低点，甚至可能无法收敛或者发散

如果已经在局部最优点，参数θ将不再改变

梯度下降时斜率会变小，参数θ更新的幅度也会变小

梯度下降法会自动采用更小的幅度，当接近局部最小点时导数值会自动变得越来越小，没必要另外减小

4

 多元线性回归：

例如关于房子的，不仅仅有房子的大小，还有卧室的数量，房子的年龄如下图所示：

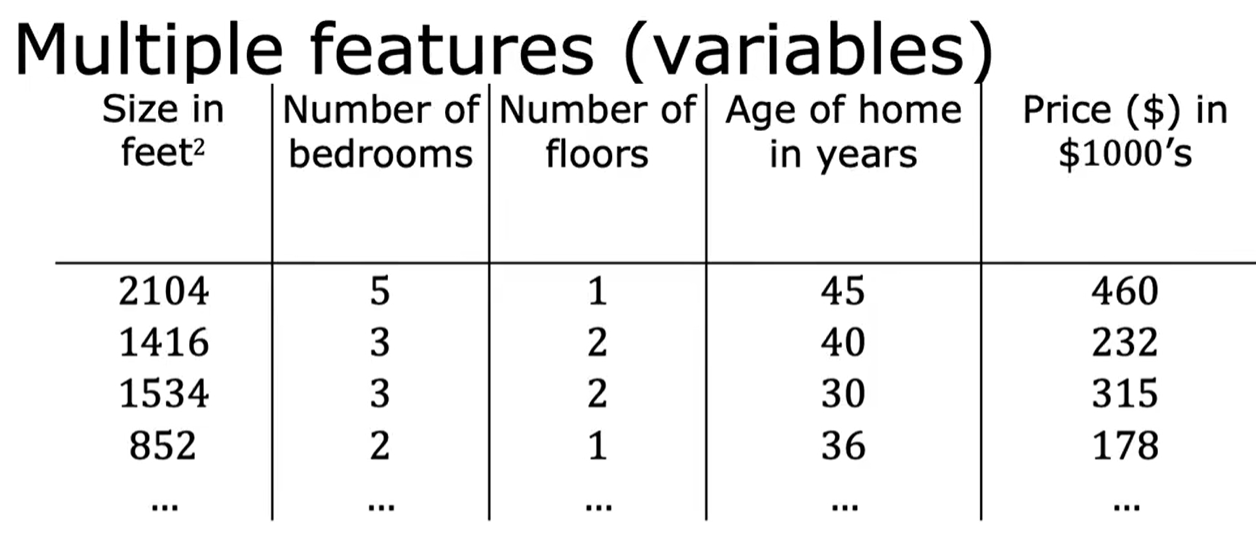
X1表示房子的大小，x2表示卧室的数量……

N为特征的总数，n=4

表示第几个行变量，x上标为3 表示 1534 3 2 30 315

表示行变量的第i个行变量里面第J个数

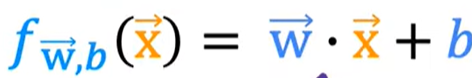
点表示为线性代数的点积

矢量化（Veatorization）：

代码变得更短

如何实现：计算机可以得到W和X的所有值，它可以同时并行的将每对W和X

相乘

梯度下降带有矢量化的多元线性回归：

                               

w1等同于对x1的偏导，共有n个x所以一直到wn

正规方程（the normal equation）：

仅适用于线性回归

缺点：如果特征数量很大，也会运行的很慢

特征缩放：

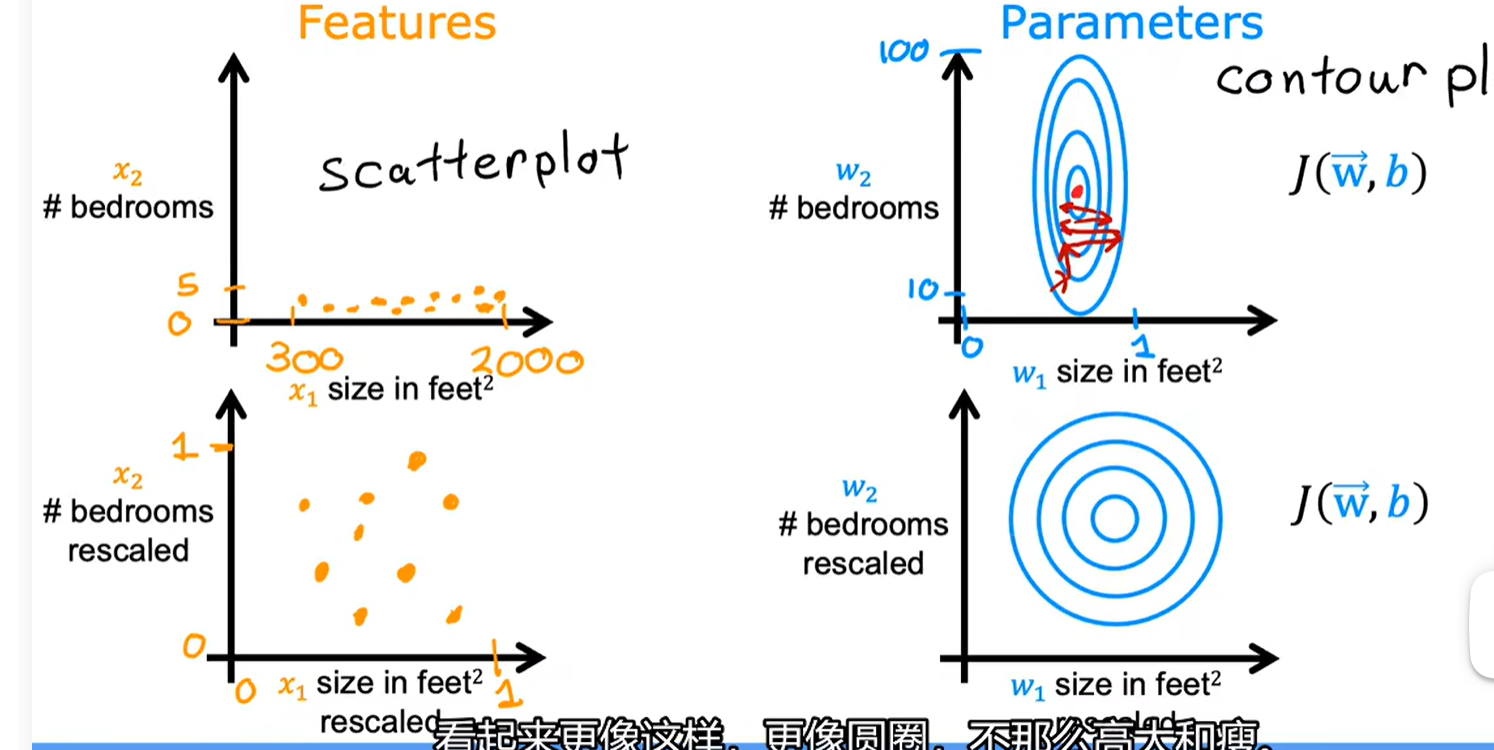
如图所示，上面两个图的比例不协调，x2的范围过大，导致w1的过于扁

将x2的范围进行缩小便是特征缩小

特征缩放：

（1）均值归一体化：使以0为中心，均位于正一负一之间

先计算均值，新的X1为（X1-均值）/（最大值-最小值）

如下图

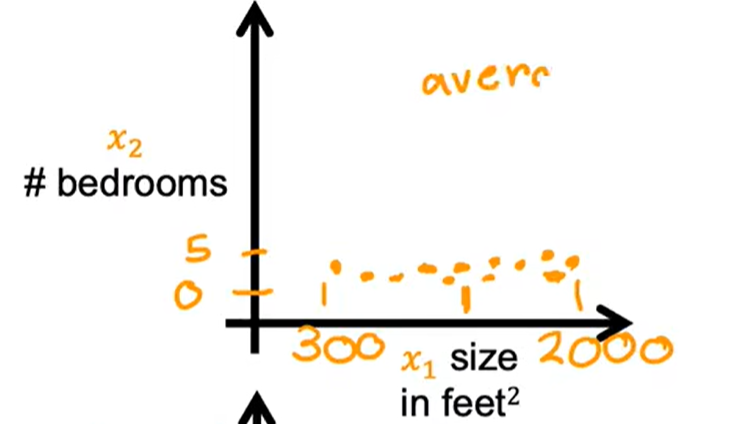
我们假设X1的均值为600，则X1为

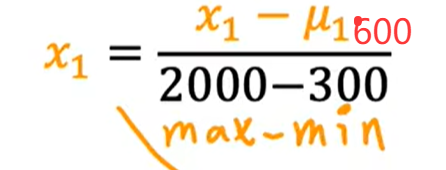
将X等于300带入X1,可以得到X1的取值范围为-0.18<=X1<=0.82

设X2的均值为2.3，同理 -0.46<=X2<=0.54

(2)Z-score标准化

计算两个特征的标准差，计算出平均值μ1，标准差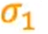，式子为,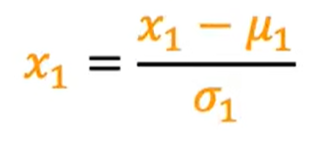

设μ1为600，为450，-0.67<=X1<=3.1，-1.6<=X2<=1.9

Z-score标准化后的数据具有均值为0、标准差为1的规律，分布形状不变，适用于正态分布数据。

判断梯度下降是否收敛：

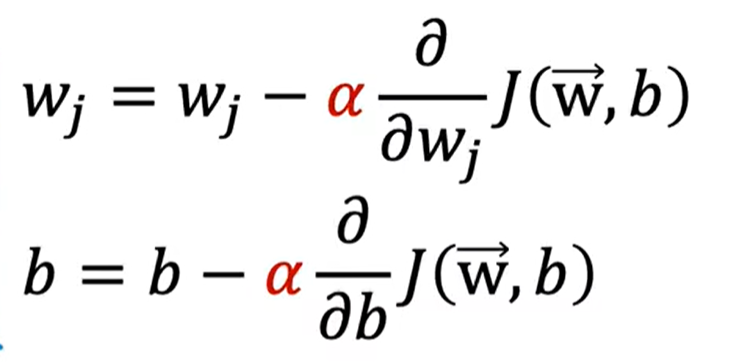
首先这是梯度下降的规则，梯度下降本身就是一种成本函数，目的是是找到最小成本化的函数J(w,b)

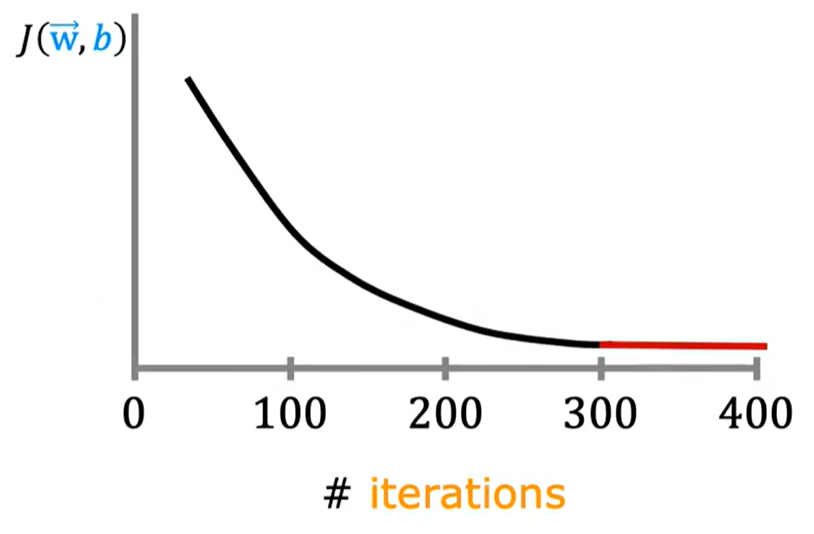
（注意横轴为迭代次数） 如图称为学习曲线            随着X轴的增大，y值应该减小，如果增大说明学习率选择错误,通过不断的迭代计算，可发现曲线越来越平稳，开始收敛。

自动收敛测试：

让a代表一个很小的数字变量，如0.001.当j(w,b)随着迭代次数增加，变化小于a 时可以说明收敛。

如何设置学习率：

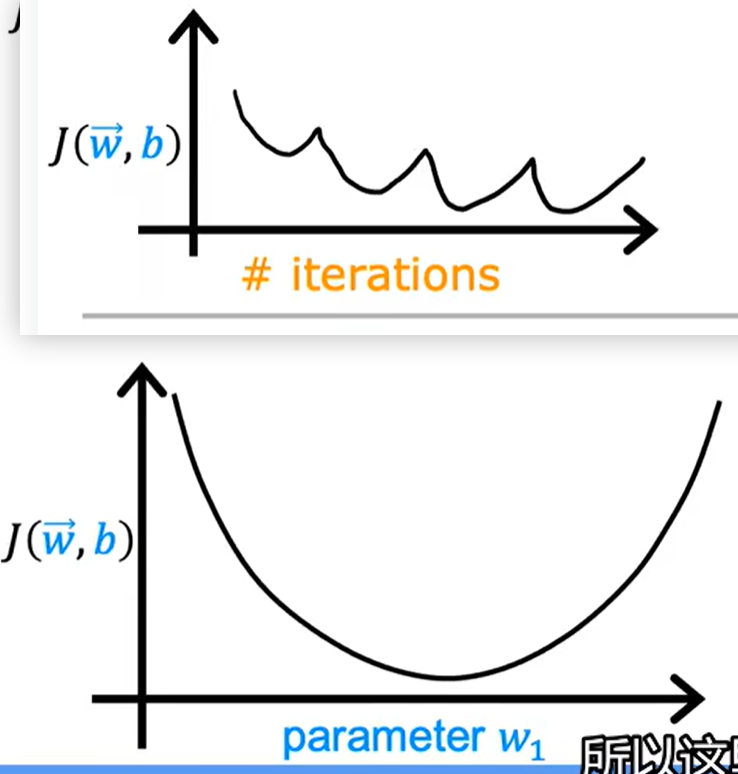
上面是学习率选择错误，下面是学习率太大

可以选择一个很小的学习率进行尝试，如0.001，然后改为0.01，0.1进行不断尝试，找出最优解。

特征工程：对于有些特征可以组合起来，可以形成新的特征。其中值的范围不可以过大与过小