392. Is Subsequence 115. Distinct Subsequences

392. Is Subsequence

Given two strings s and t, return true if s is a subsequence of t, or false otherwise.

A subsequence of a string is a new string that is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (i.e., "ace" is a subsequence of "abcde" while "aec" is not).

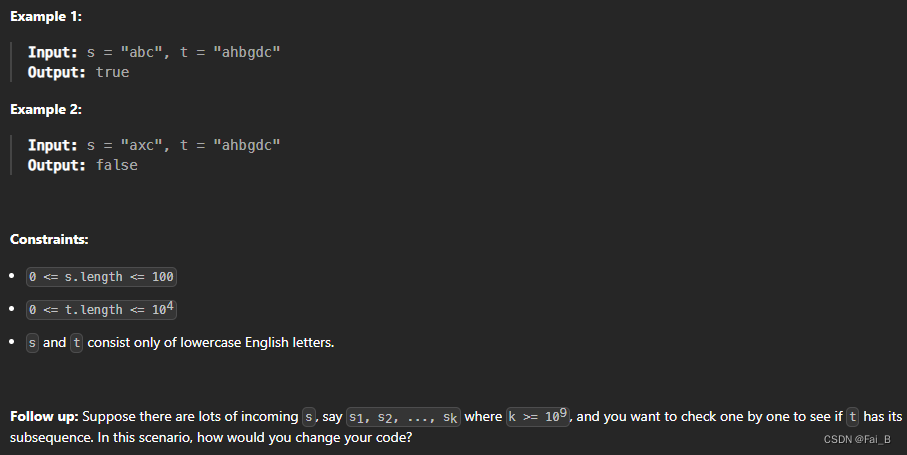
DP:

Time complexity: O(n × m)
Space complexity: O(n × m)

class Solution:
    def isSubsequence(self, s: str, t: str) -> bool:
        m = len(s)
        n = len(t)

        dp = [[0] * (n + 1) for _ in range(m + 1)]


        for i in range(1, m + 1):
            for j in range(1, n + 1):
                if s[i - 1] == t[j - 1]:
                    dp[i][j] = dp[i - 1][j - 1] + 1 
                else:
                    dp[i][j] = dp[i][j - 1]
        
        return dp[-1][-1] == m

 nomal:

class Solution:
    def isSubsequence(self, s: str, t: str) -> bool:
        i=0
        j=0
        while i<len(s) and j < len(t):
            if s[i]==t[j]:
                i+=1
            j+=1

        if i==len(s):
            return True
        return False

optimal:

class Solution:
    def isSubsequence(self, s: str, t: str) -> bool:
        if not s: return True
        j=0
        for i,ch in enumerate(t):
            if(s[j]==ch):
                j+=1
            if(j==len(s)):return True
        return False

115. Distinct Subsequences

Given two strings s and t, return the number of distinct subsequences of s which equals t.

The test cases are generated so that the answer fits on a 32-bit signed integer.

 

Analyze the two cases:

1. s[i - 1] is equal to t[j - 1].
2. s[i - 1] and t[j - 1] are not equal

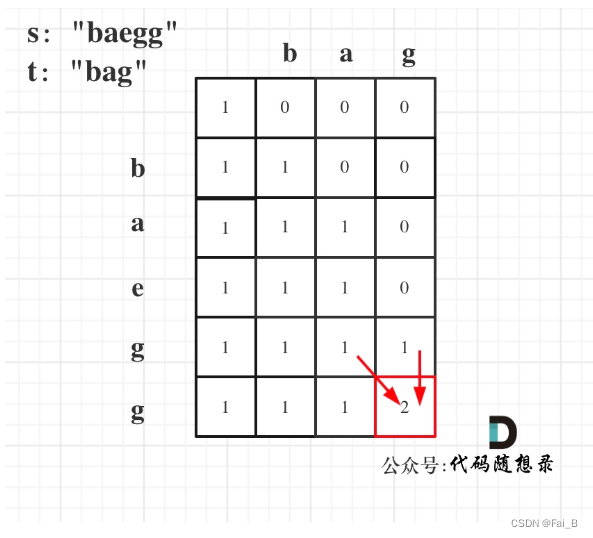
When s[i - 1] is equal to t[j - 1], dp[i][j] can have two parts.

One part is to match with s[i - 1], then the number is dp[i - 1][j - 1]. That is, there is no need to consider the last letter of the current s-substring and t-substring, so only dp[i - 1][j - 1] is needed.

A part of it is matched without using s[i - 1], and the number is dp[i - 1][j].

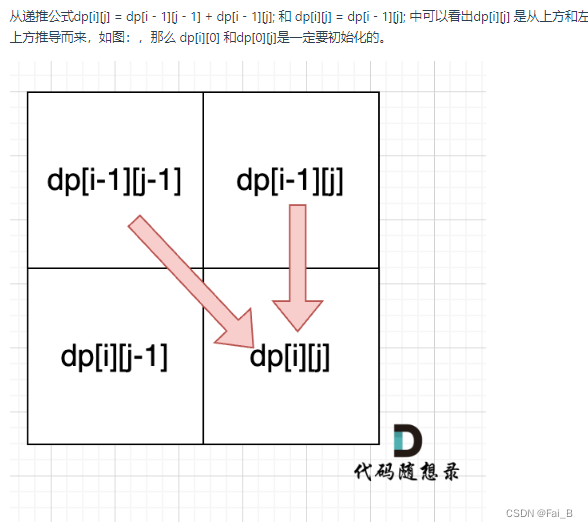
When s[i - 1] == t[j - 1] , dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];

When s[i - 1] != to t[j - 1], dp[i][j] is only partially composed and does not have to be matched by s[i - 1] (that is, it is simulated to remove this element in s), i.e.: dp[i - 1][j]

So the recursive formula is: dp[i][j] = dp[i - 1][j]

 

 DP:

Time complexity: O(n × m)
Space complexity: O(n × m)

class Solution:
    def numDistinct(self, s: str, t: str) -> int:
        dp = [[0] * (len(t)+1) for _ in range(len(s)+1)]
        for i in range(len(s)):
            dp[i][0] = 1
        for j in range(1, len(t)):
            dp[0][j] = 0
        for i in range(1, len(s)+1):
            for j in range(1, len(t)+1):
                if s[i-1] == t[j-1]:
                    dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
                else:
                    dp[i][j] = dp[i-1][j]
        return dp[-1][-1]

 optimal:

Time complexity: O(n × m)
Space complexity: O(n)

def numDistinct(self, s: str, t: str) -> int:
        n1, n2 = len(s), len(t)
        if n1 < n2:
            return 0

        dp = [0 for _ in range(n2 + 1)]
        dp[0] = 1

        for i in range(1, n1 + 1):
            # 必须深拷贝
            # 不然prev[i]和dp[i]是同一个地址的引用
            prev = dp.copy()
            # 剪枝，保证s的长度大于等于t
            # 因为对于任意i，i > n1, dp[i] = 0
            # 没必要跟新状态。 
            end = i if i < n2 else n2
            for j in range(1, end + 1):
                if s[i - 1] == t[j - 1]:
                    dp[j] = prev[j - 1] + prev[j]
                else:
                    dp[j] = prev[j]
        return dp[-1]