669. Trim a Binary Search Tree 108. Convert Sorted Array to Binary Search Tree 538. Convert BST to G

669. Trim a Binary Search Tree 修剪BST

Given the root of a binary search tree and the lowest and highest boundaries as low and high, trim the tree so that all its elements lies in [low, high]. Trimming the tree should not change the relative structure of the elements that will remain in the tree (i.e., any node's descendant should remain a descendant). It can be proven that there is a unique answer.

Return the root of the trimmed binary search tree. Note that the root may change depending on the given bounds.

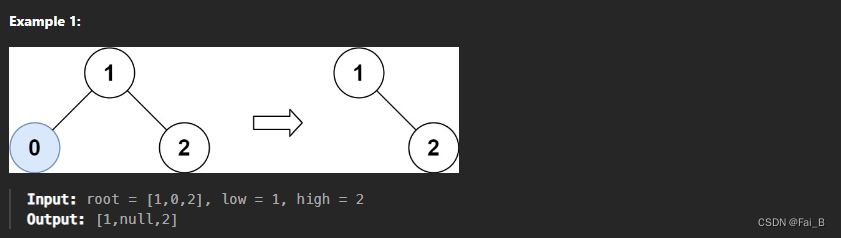
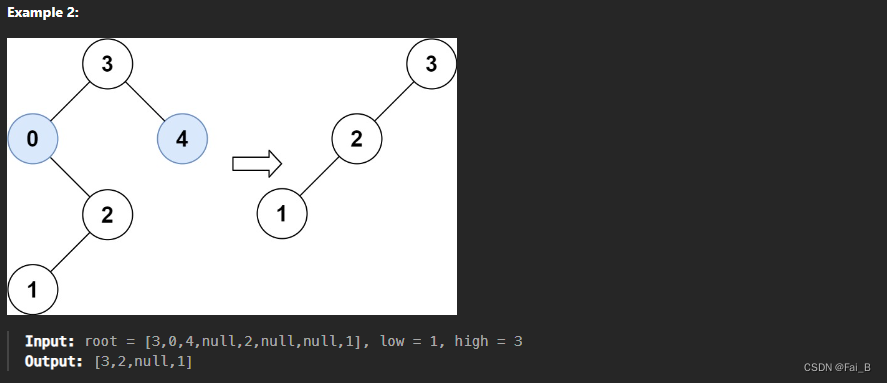
recursive:

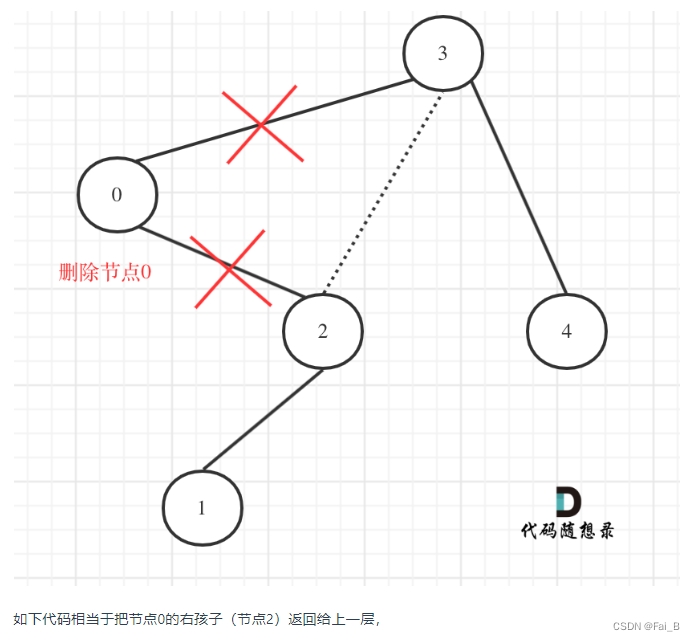
class Solution:
    def trimBST(self, root: TreeNode, low: int, high: int) -> TreeNode:
        if root is None:
            return None
        if root.val < low:
            # 寻找符合区间 [low, high] 的节点
            return self.trimBST(root.right, low, high) #节点的右孩子给上一层
        if root.val > high:
            # 寻找符合区间 [low, high] 的节点
            return self.trimBST(root.left, low, high)
        root.left = self.trimBST(root.left, low, high)  # root.left 接入符合条件的左孩子
        root.right = self.trimBST(root.right, low, high)  # root.right 接入符合条件的右孩子
        return root

iteration:

class Solution:
    def trimBST(self, root: TreeNode, L: int, R: int) -> TreeNode:
        if not root:
            return None
        
        # 处理头结点，让root移动到[L, R] 范围内，注意是左闭右闭
        while root and (root.val < L or root.val > R):
            if root.val < L:
                root = root.right  # 小于L往右走
            else:
                root = root.left  # 大于R往左走
        
        cur = root
        
        # 此时root已经在[L, R] 范围内，处理左孩子元素小于L的情况
        while cur:
            while cur.left and cur.left.val < L:
                cur.left = cur.left.right
            cur = cur.left
        
        cur = root
        
        # 此时root已经在[L, R] 范围内，处理右孩子大于R的情况
        while cur:
            while cur.right and cur.right.val > R:
                cur.right = cur.right.left
            cur = cur.right
        
        return root

108. Convert Sorted Array to Binary Search Tree

Given an integer array nums where the elements are sorted in ascending order, convert it to a 

height-balanced binary search tree.

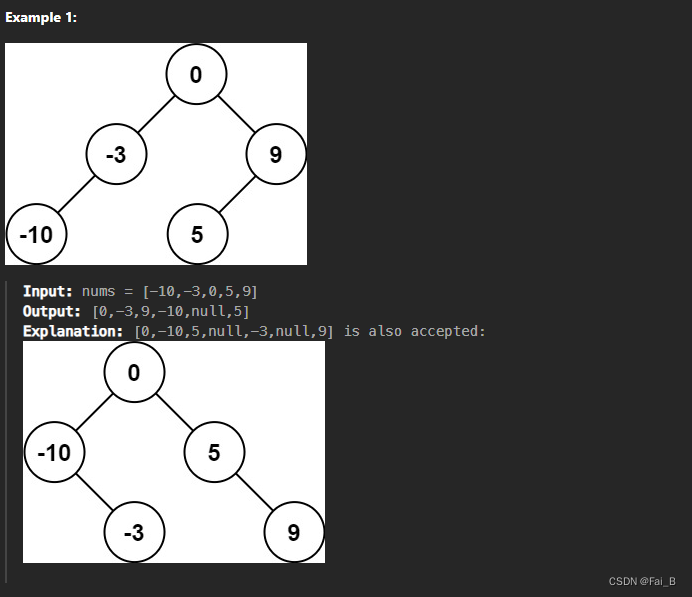
recursion:

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
        if len(nums) == 0:
            return None
        
        mid = len(nums)//2
        root_val = nums[mid]
        root = TreeNode(root_val)

        root.left = self.sortedArrayToBST(nums[:mid]) #wrong [: mid-1]
        root.right = self.sortedArrayToBST(nums[mid+1:])
        
        return root

 wrong answer:  There will always be only three nodes: root, left, and right.

class Solution:

    def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:

        if len(nums) == 0:

            return None

       

        mid = len(nums)//2

        root_val = nums[mid]

        root = TreeNode(root_val)

        for i in range(mid-1, -1, -1):

            root.left = TreeNode(nums[i])

        for i in range(mid+1, len(nums)):

            root.right = TreeNode(nums[i])

       

        return root 

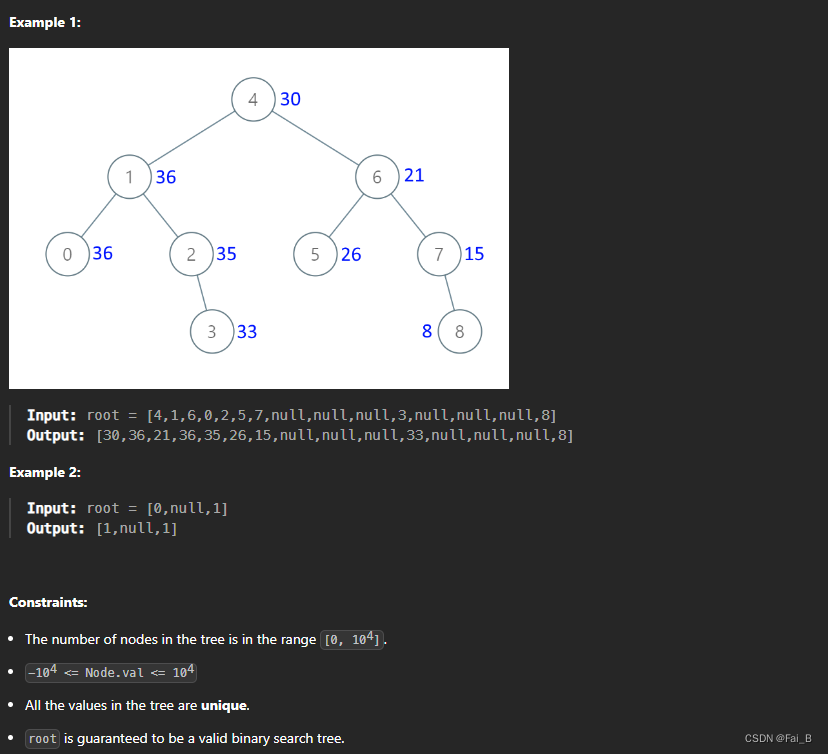
 538. Convert BST to Greater Tree

Given the root of a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus the sum of all keys greater than the original key in BST.

As a reminder, a binary search tree is a tree that satisfies these constraints:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.
• Both the left and right subtrees must also be binary search trees.

1. right -> root -> left: traversal order; def traversal:

2. pre : Record the value of the previous node; def  __init__

3.recursion

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        pre = 0
        self.traversal(root)
        return root
    
    def traversal(self, root):
        if not root:
            return
        self.traversal(root.right)
        root.val += self.pre
        self.pre = root.val
        self.traversal(root.left)

    def __init__(self, pre = None):
        self.pre = 0    # 记录前一个节点的数值

iteration: right -> root -> left

class Solution:
    def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        if not root: return root
        stack = []
        result = []
        cur = root
        pre = 0
        while cur or stack:
            if cur:
                stack.append(cur)
                cur = cur.right
            else: 
                cur = stack.pop()
                cur.val+= pre # 右
                pre = cur.val #中
                cur =cur.left #左
        return root