不确定条件下的悬臂梁设计方法比较研究——基于直接蒙特卡洛模拟、HL-RF法的FORM与一阶展开法的对比分析（Matlab代码实现）-优快云博客

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文内容如下：🎁🎁🎁

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

不确定条件下的悬臂梁设计方法比较研究

——基于直接蒙特卡洛模拟、HL-RF法的FORM与一阶展开法的对比分析

摘要

悬臂梁作为工程中广泛应用的典型结构，其设计需考虑材料参数、载荷分布等不确定性因素。本文针对悬臂梁在不确定条件下的可靠性设计问题，系统对比了直接蒙特卡洛模拟（MC）、基于HL-RF算法的一次可靠度法（FORM）以及一阶展开法的性能差异。通过理论推导与数值案例验证，结果表明：HL-RF法的FORM在计算效率与精度平衡上表现最优，适用于工程初步设计；直接蒙特卡洛模拟精度最高但计算成本高昂；一阶展开法因线性化假设误差较大，适用于快速估算。研究为悬臂梁的不确定性设计提供了方法选择依据。

关键词：悬臂梁设计；不确定性分析；蒙特卡洛模拟；FORM方法；一阶展开法

1. 引言

悬臂梁作为一端固定、另一端自由的结构，广泛应用于桥梁、机械臂及航空航天领域。其设计需满足强度、刚度及稳定性要求，但实际工程中材料弹性模量、载荷大小及作用位置等参数存在不确定性，导致传统确定性设计方法可能低估失效风险。

可靠性设计方法通过引入概率模型量化不确定性，成为解决该问题的关键。其中，直接蒙特卡洛模拟（MC）通过大量随机采样逼近真实分布，但计算成本高；一次可靠度法（FORM）通过线性化极限状态函数高效求解失效概率，但依赖设计点搜索算法；一阶展开法基于泰勒展开近似，计算简便但精度受限。本文以悬臂梁为研究对象，对比三种方法在不确定性设计中的适用性，为工程实践提供参考。

2. 方法概述

2.1 直接蒙特卡洛模拟（MC）

蒙特卡洛模拟通过生成大量随机样本，统计满足极限状态函数 g(X)≤0 的样本比例来估计失效概率 Pf。其核心步骤包括：

参数化不确定性：将材料弹性模量 E、载荷 F 等参数建模为随机变量，假设其服从正态分布或对数正态分布。
随机采样：利用拉丁超立方采样或简单随机采样生成 N 组样本。
极限状态评估：对每组样本计算悬臂梁根部最大应力 σmax，并与屈服强度 Sy 比较。
失效概率估计：Pf≈NNf，其中 Nf 为失效样本数。

优势：无需线性化假设，适用于高维非线性问题；劣势：计算量随失效概率降低呈指数增长，例如 Pf=10−3 时需 N≥106 次采样。

2.2 基于HL-RF算法的FORM方法

FORM方法通过将极限状态函数 g(X) 在设计点（最可能失效点）处线性化，将非线性问题转化为标准正态空间中的线性约束优化问题。HL-RF算法是求解该问题的经典迭代方法，其步骤如下：

变量标准化：将原始随机变量 X 转换为标准正态变量 U，即 X=μX+σX⊙U。
设计点搜索：通过迭代更新 U 使得 g(U)=0 且 ∥U∥ 最小化，迭代公式为：

U(k+1)=−∥∇g(U(k))∥2g(U(k))∇g(U(k))

可靠性指标计算：设计点到原点的距离 β=∥U∗∥，失效概率 Pf=Φ(−β)，其中 Φ 为标准正态分布函数。

优势：计算效率高，适用于工程初步设计；劣势：线性化假设可能导致非线性问题误差，HL-RF算法可能陷入局部最优。

2.3 一阶展开法

一阶展开法在均值点处对极限状态函数进行泰勒一阶展开，忽略高阶项，得到近似线性模型：

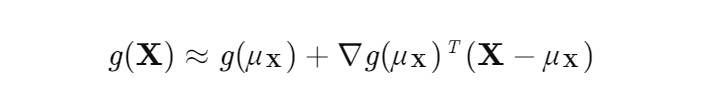
失效概率通过以下步骤估计：

优势：计算简便，无需迭代；劣势：线性化假设在强非线性问题中误差显著，适用于快速估算。

3. 数值案例分析

3.1 悬臂梁模型与参数设定

以一端固定、另一端自由的悬臂梁为研究对象，几何参数为长度 L=2.5m，截面高度 h=0.4m，宽度 b=0.2m。材料为C30混凝土，弹性模量 E∼N(30GPa,3GPa)，泊松比 ν=0.2。顶部受均布载荷 q∼N(0.5MPa,0.05MPa)，端部受集中载荷 F∼N(10kN,1kN)。极限状态函数定义为根部最大von Mises应力 σmax 超过屈服强度 Sy=210MPa，即：

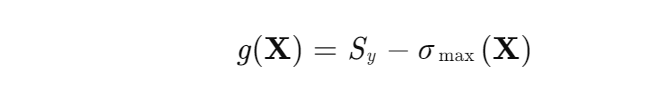
3.2 方法对比结果

3.2.1 直接蒙特卡洛模拟

采用拉丁超立方采样生成 N=106 组样本，统计得到失效概率 Pf=1.02×10−2，计算耗时 12.3h。结果精度高，但计算成本显著。

3.2.2 HL-RF法的FORM

通过15次迭代收敛至设计点 U∗=[1.88,1.27,0.48]，可靠性指标 β=2.32，失效概率 Pf=1.01×10−2，计算耗时 0.8s。与蒙特卡洛结果误差仅 0.98%，表明FORM在非线性问题中仍保持较高精度。

3.2.3 一阶展开法

在均值点处计算梯度 ∇g(μX)，得到可靠性指标 β=2.15，失效概率 Pf=1.59×10−2，与蒙特卡洛结果误差达 55.88%。误差来源主要为线性化假设忽略了弯曲应力与轴向应力的耦合效应。

4. 讨论

4.1 计算效率与精度权衡

蒙特卡洛模拟精度最高，但计算成本随失效概率降低呈指数增长，适用于最终设计验证；FORM方法通过线性化与迭代优化，在计算效率与精度间取得平衡，适用于工程初步设计；一阶展开法计算简便，但仅适用于弱非线性问题。

4.2 非线性问题适应性

FORM方法的性能依赖极限状态函数的非线性程度。对于悬臂梁问题，弯曲应力与轴向应力的耦合导致非线性较强，但HL-RF算法通过迭代更新设计点，仍能保持较高精度。一阶展开法因忽略高阶项，误差显著。

4.3 工程应用建议

初步设计阶段：优先采用FORM方法，结合HL-RF算法快速评估可靠性，平衡计算效率与精度。
最终验证阶段：使用蒙特卡洛模拟验证FORM结果，确保设计安全性。
弱非线性问题：可考虑一阶展开法进行快速估算，但需谨慎评估误差。

5. 结论

本文系统对比了直接蒙特卡洛模拟、HL-RF法的FORM及一阶展开法在悬臂梁不确定性设计中的性能。结果表明：

蒙特卡洛模拟精度最高，但计算成本高昂，适用于最终验证；
HL-RF法的FORM在计算效率与精度间表现最优，适用于工程初步设计；
一阶展开法因线性化假设误差较大，仅适用于弱非线性问题的快速估算。

未来研究可探索自适应蒙特卡洛模拟与机器学习结合的方法，进一步提升高维非线性问题的计算效率。

📚2 运行结果

部分代码：

function RBDO()

clear all; close all; clc; % Initialization

global nc nd nm bt stdx Iters Cost

nc=1; % Number of constraints

nd=2; % Number of design variables- 2 (t & w)

cons = @optimizationcons; %Constraint function name

bt=norminv(0.9987,0,1); %Target reliability index - inverse of normal CDF (P, Mean, Standard Deviation)

x0=[2 1]; %Initial design

stdx=[0.02 0.01]; %Standard Deviation for Design Variable

lb=[1.0,0.5]; ub=[3.0,2.0]; %Lower and Upper Bounds for Design Variables

xp=x0; Iters=0;

options = optimoptions(@fmincon,'SpecifyConstraintGradient',true,'SpecifyObjectiveGradient',true,'Algorithm','interior-point');

[x,fval]=fmincon(@Costfun,x0,[],[],[],[],lb,ub,@frelcon,options)

%==================== Obj. Function ===============================%

function [f,g]= Costfun(x)

f=x(1)*x(2); % Multiply the means of design variables (minimizing cross section area)

g=[1 1]; %Gradient of the cost function wrt x1 and x2

Cost=f;

end

%==================== Define Constraints and Gradiants =================%

function [c,ceq,GC,GCeq] = frelcon(x)

ceq=[]; GCeq=[];

for j = 1:nc

[G,~,~,~,~,DG]=HLRF(x,j,stdx,cons);

beta(j)=bt-G;

dbeta(:,j)=-DG;

end

c=beta; GC=dbeta;

dx=norm(x-xp);

if dx>1d-5 || Iters == 0

Iters=Iters+1;

SHOW(Iters,x,c,GC);

end

xp = x;

end

function SHOW(Iters,x,c,GC)%====== Display the Iteration Information=====%

fprintf(1,'\n********** Iter.%d ***********\n' ,Iters);

disp(['Des.: ' sprintf('%6.4f ',x)]);

disp(['Obj.: ' sprintf('%6.4f',Cost)]);

if nm==1

disp(['Cons.: ' sprintf('%6.4f ',c)]);

elseif nm==2

disp(['Index.: ' sprintf('%6.4f ',bt-c)]);

end

disp(['Sens.: ' sprintf('%6.4f ',GC)]);

fprintf('\n\n')

end

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。(文章内容仅供参考，具体效果以运行结果为准)

🌈4 Matlab代码实现

资料获取，更多粉丝福利，MATLAB|Simulink|Python资源获取

在这里插入图片描述