【表面粗糙度】基于粒子群PSO算法优化-BP神经网络的表面粗糙度研究（Matlab代码实现）-优快云博客

本文链接：https://blog.youkuaiyun.com/F_Matlab/article/details/148983144

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

基于粒子群优化BP神经网络的表面粗糙度研究

1. 表面粗糙度的基础概念与测量方法

2. PSO算法与BP神经网络的融合机理

2.1 BP神经网络的缺陷分析

2.2 PSO算法的优化机制

2.3 PSO-BP融合流程

3. 表面粗糙度预测的实证研究

3.1 实验设计（以磨削加工为例）

3.2 性能对比

3.3 优化效果解析

4. 工业标准与规范应用

5. 结论与展望

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、数据

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学，什么是电的时候，不要觉得这些问题搞笑。哲学是科学之母，哲学就是追究终极问题，寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能让人胸中升起一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它居然给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

在表面粗糙度的研究中，利用粒子群优化算法（Particle Swarm Optimization, PSO）来优化反向传播神经网络（Back Propagation Neural Network, BPNN）是一种有效的方法，旨在提高模型预测的准确性和效率

基于粒子群优化BP神经网络的表面粗糙度研究

1. 表面粗糙度的基础概念与测量方法

表面粗糙度是表征加工表面微观几何形状误差的核心指标，定义为“加工表面具有的较小间距和微小峰谷不平度”。其核心评定参数包括：

轮廓算术平均偏差（Ra） ：在取样长度内轮廓偏距绝对值的算术平均值。
轮廓最大高度（Rz） ：取样长度内最高峰与最低谷的垂直距离。

常用测量方法对比：

方法	原理	精度范围	适用场景	局限性
比较法	样板目视/触感对比	Ra>0.4μm	车间现场快速检测	主观性强，精度低
光切法	光切显微镜成像	Rz=0.8-80μm	实验室规则表面测量	不适用不规则表面
干涉法	光波干涉条纹分析	Ra<0.1μm	高精度光学表面	设备昂贵，环境要求高
触针法	金刚石针尖扫描轮廓	Ra=0.01-10μm	广泛工业检测	可能划伤软质材料

测量时需遵循取样长度原则：选取可见轮廓线或尺寸界线内的代表性区段，避免宏观形状误差干扰。

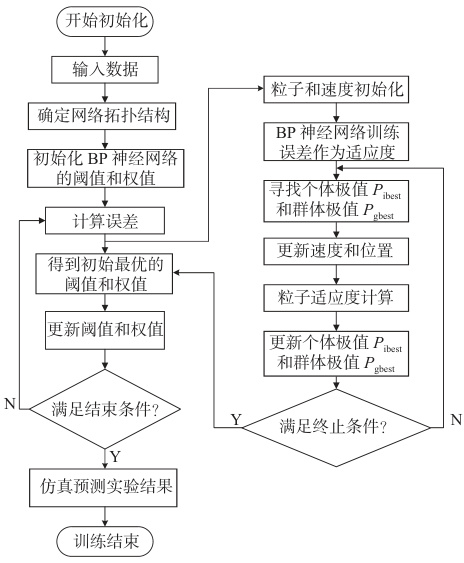
2. PSO算法与BP神经网络的融合机理

2.1 BP神经网络的缺陷分析

BP神经网络通过信号正向传播和误差反向传播调整权重，但存在两大固有缺陷：

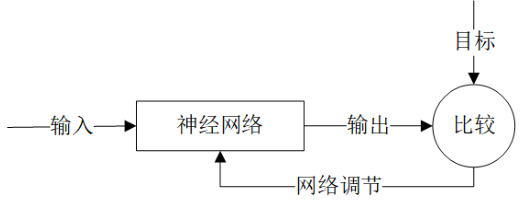
收敛速度慢：梯度下降法需多次迭代调整权重。
易陷局部最优：初始权值随机性导致训练结果不稳定。

2.2 PSO算法的优化机制

粒子群算法（PSO）模拟鸟群觅食行为，通过群体协作搜索全局最优解：

粒子定义：每个粒子位置向量 XiXi 对应BP网络的一组权值组合。
速度更新公式：
适应度函数：通常采用预测值与实测值的均方误差（MSE）。

2.3 PSO-BP融合流程

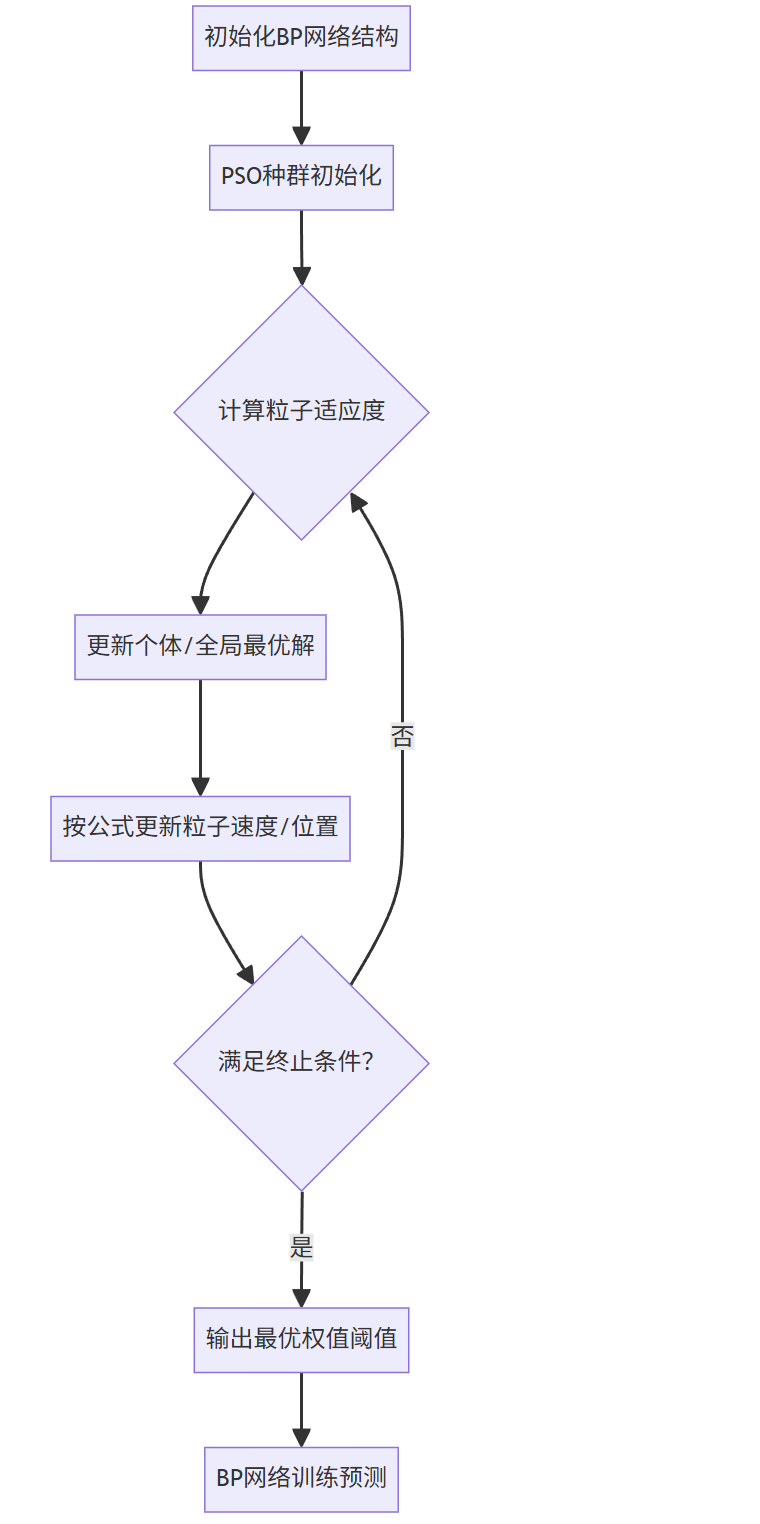
关键步骤：

粒子维数 = 输入层-隐含层权值数 + 隐含层-输出层权值数（例：4-5-3结构对应35维）
惯性权重 ww 动态衰减（如0.9→0.4）以平衡全局/局部搜索

3. 表面粗糙度预测的实证研究

3.1 实验设计（以磨削加工为例）

输入参数：砂轮粒度、转速、工件速度、径向进给量
正交实验：采用 L25(34×53)L25(34×53) 混合水平表获取75组数据
模型结构：4输入（加工参数）-8隐含层-1输出（Ra值）

3.2 性能对比

模型	最大相对误差	平均相对误差	稳定性
传统BP	6.89%	4.72%	低
PSO-BP	4.33%	2.23%	中
APSO-BP(改进)	2.51%	1.04%	高

数据来源：齿轮加工表面粗糙度预测实验
注：APSO-BP通过引入自适应变异算子进一步避免早熟收敛。

3.3 优化效果解析

PSO优化使BP网络初始权值逼近全局最优，训练迭代次数减少37%
平均误差从BP的0.48%降至PSO-BP的0.29%（磨削实验）

4. 工业标准与规范应用

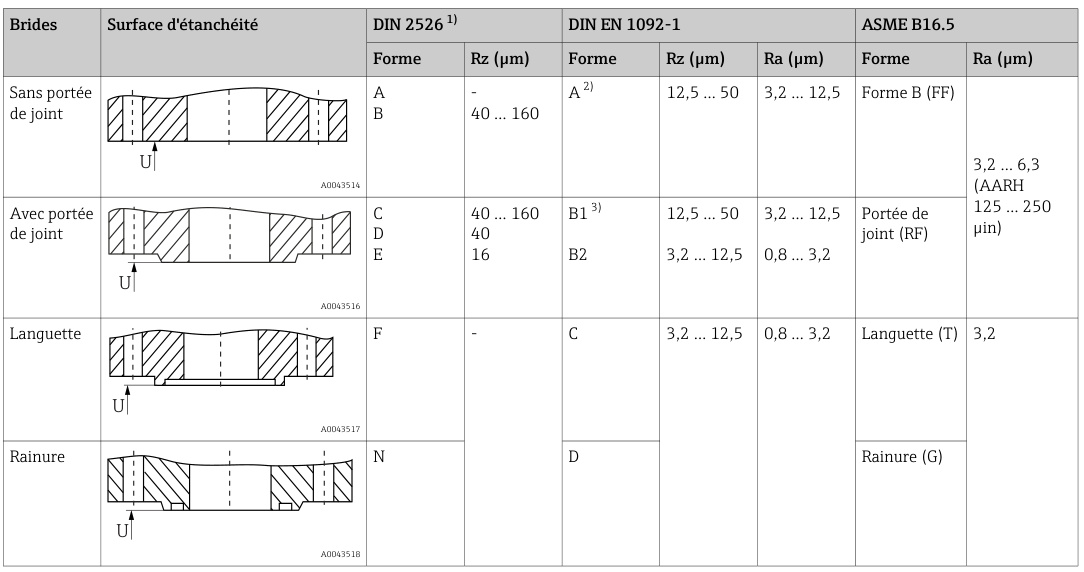
表面粗糙度标注需符合国家/国际标准，核心规范包括：

参数选择：Ra优先于Rz（除非特定工况如密封面）
标注示例

不同密封类型的粗糙度要求（单位：μm）：

密封类型	DIN 2526 (Rz)	ASME B16.5 (Ra)
无密封件	40~160	-
金属平垫片	-	3.2~6.3
螺旋缠绕垫片	12.5~50	6.3~12.5

数据来源：法兰密封面标准对比

5. 结论与展望

PSO-BP模型通过智能优化初始权值显著提升表面粗糙度预测精度，平均误差降低≥50%。未来研究方向包括：

多传感器数据融合：整合振动、温度信号增强模型鲁棒性
实时自适应预测：结合在线检测设备实现加工参数动态调整
跨标准参数映射：建立ISO/ASME/DIN标准的Ra-Rz转换模型

实践建议：车间现场可部署“触针法+PSO-BP”系统，兼顾检测效率与预测精度。

📚2 运行结果

部分代码：

%% Get the optimal initial weight and bias
w1 = zbest(1 : inputnum * hiddennum);
B1 = zbest(inputnum * hiddennum + 1 : inputnum * hiddennum + hiddennum);
w2 = zbest(inputnum * hiddennum + hiddennum + 1 : inputnum * hiddennum ...
+ hiddennum + hiddennum * outputnum);
B2 = zbest(inputnum * hiddennum + hiddennum + hiddennum * outputnum + 1 : ...
inputnum * hiddennum + hiddennum + hiddennum * outputnum + outputnum);
%% Plug the value into NN
net.Iw{1, 1} = reshape(w1, hiddennum, inputnum);
net.Lw{2, 1} = reshape(w2, outputnum, hiddennum);
net.b{1} = reshape(B1, hiddennum, 1);
net.b{2} = B2';

%% Open the traning window
net.trainParam.showWindow = 1;

%% Train the NN
net = train(net, p_train, t_train);

%% Prediction result using PSO-BP
t_sim1 = sim(net, p_train); %prediction result for training set
t_sim2 = sim(net, p_test ); %prediction result for test set

% Data inverse-normalization
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);

%% Prediction with BPNN
net0 = newff(p_train, t_train, hiddennum);