基础图算法:广度搜索优先(BFS)

什么是图?这里有对图的描述https://www.jianshu.com/p/bce71b2bdbc8

那么广度搜索优先算法与深度搜索优先算法的作用就是遍历整个图数据的两种算法，两种算法的核心都是对图的遍历,都属于对贪心算法的体现。

广度优先算法(BFS又称为宽度优先算法)

广度优先算法是遍历完整图的一种遍历算法，也是很多高级算法的基础,例如Dijkstra又称迪杰斯特拉算法(用来计算正向最短路径算法),Kruskal 又称克鲁斯卡尔算法(用来计算最小生成树)。BFS算法的核心类似于广播形式的由内到外一层一层进行搜索。直到遍历最外一层结构。通常我们需要依赖与队列(先进先出)数据结构完成整体的遍历。后面我会通过实际的栗子来介绍BFS的应用场景和实际用处。

如图所示为一个基本图

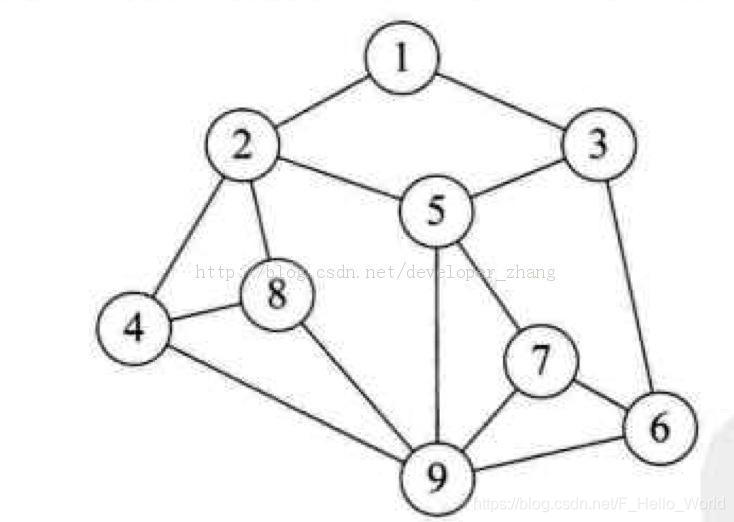
如何区遍历以上图结构.

第一步:准备创建一个空队列中,以及一个能保证数据唯一性的集合(我这里用set保存值为顶点id)来保存遍历过的点,我们假设以1顶点为(可以从任意顶点开始)开始，将其放入队列中。

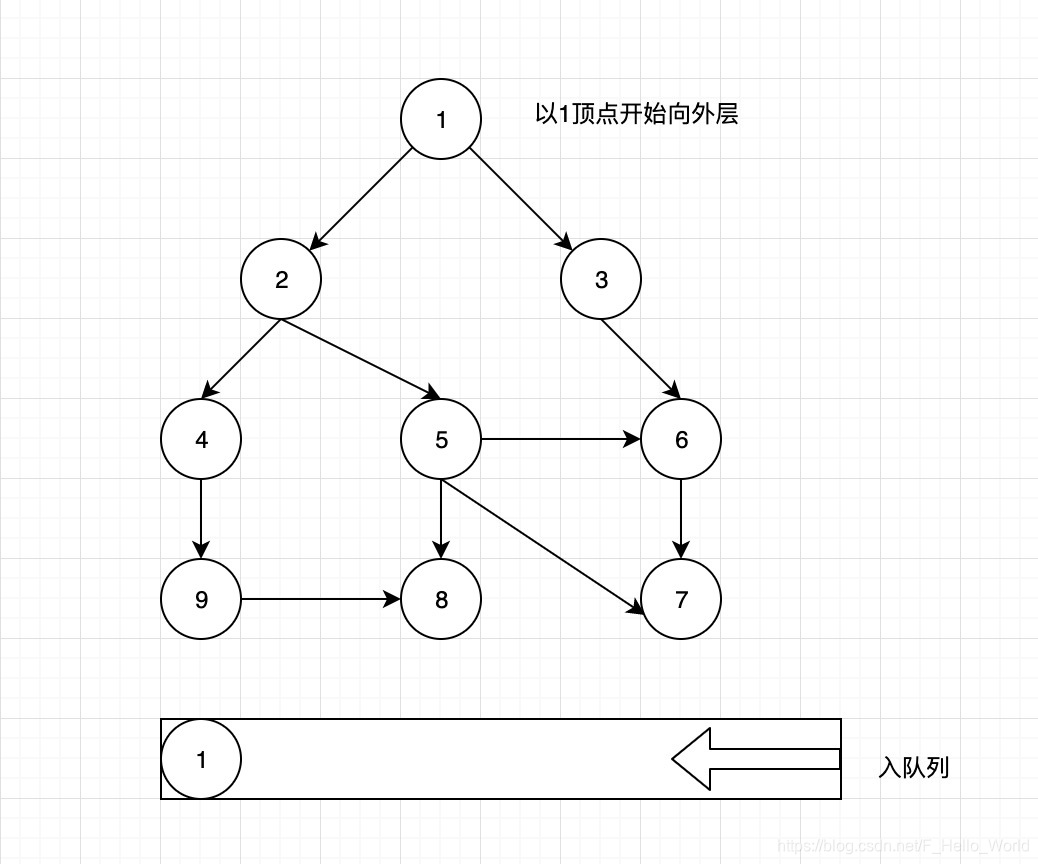
第二步:从队列中获取1顶点，获取1顶点下连接的2，3点。判断是否在set中已存在该顶点，如果不存在写入到队列中。此时第一层已遍历完成。

第三步:从队列中取出2顶点，获取2顶点下连接4,5,6顶点,并判断是该顶点否在set中已存在，如果不存在则写入到队列中。再拿出3顶点获取5，7顶点，因为5顶点再set中已存在，不需要再写入队列.此时第二层已遍历完成

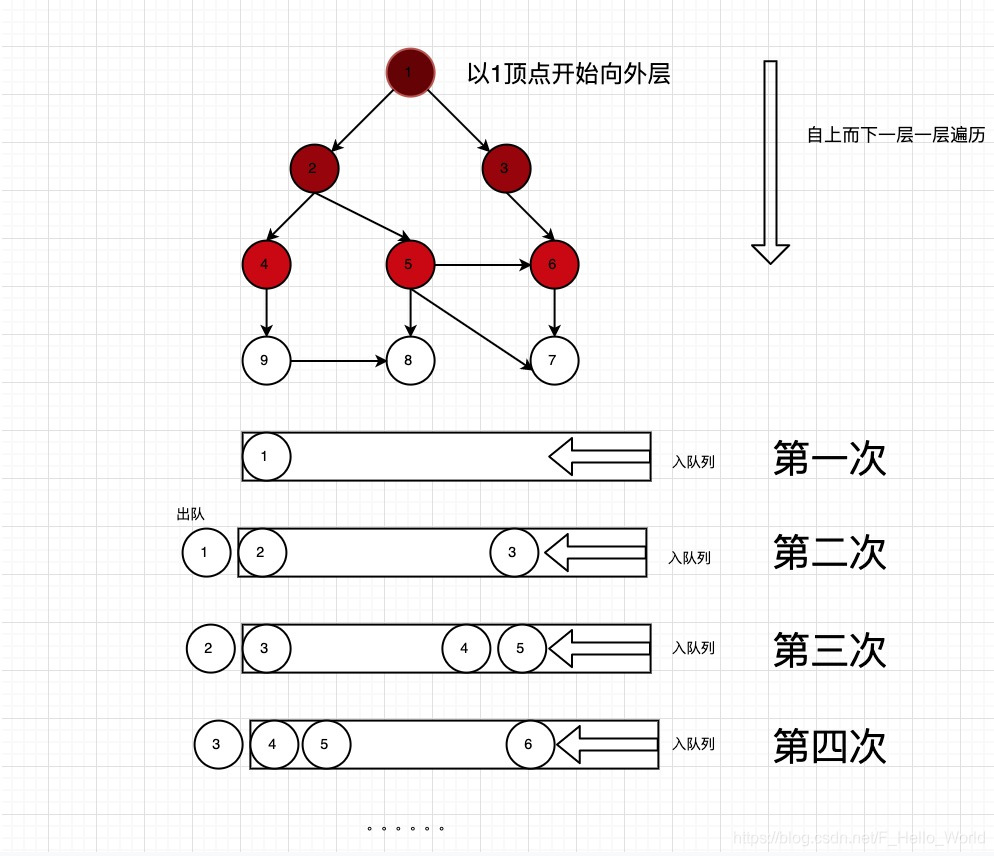
循环取出队列中的顶点，直到最后队列为空队列此时，所有图中顶点已遍历成功

对于整个图结构遍历的时间复杂度为O(n+e) n为节点数 e为边数

 

在我们的项目中有以下需求图如下所示:当我们要删除D顶点时，我们要级连删除D顶点 。已知顶点集合,边集合。

解决思路:先移除被删除点以及与顶点关联边数据，通过BFS算法获取图中取出删除点后仍然与A点关联的其它顶点即可

这里通过JAVA代码实现

1:定义图,边,顶点实体类

package com.demo.kafkaDemo.BFS;

import lombok.*;

import java.io.Serializable;
import java.util.List;

@Builder
@AllArgsConstructor
@NoArgsConstructor
@Setter
@Getter
public class Graphs implements Serializable {

        //节点列表 包含所有节点信息
        private List<Graphs.Vertex> vertexs;

        //关系信息
        private List<Graphs.Edge> edges;

        @Data
        @Builder
        @NoArgsConstructor
        @AllArgsConstructor
        public static class Vertex implements Serializable {

            //是否为主节点
            private boolean isMaster = false;

            //顶点id
            private String id;

            //顶点描述
            private String content;

        }

        @Data
        @Builder
        @NoArgsConstructor
        @AllArgsConstructor
        /**
         * 关系描述 记录起始-到终止几点的关系描述
         */
        public static class Edge implements Serializable {
            //起始顶点-Id
            private String from;

            //终止顶点-Id
            private String to;

            //顶点关系描述
            private String description;

        }
        
    }

2:构建测试数据,以及实现功能需求

import java.util.*;
import java.util.stream.Collectors;

import static com.sun.org.apache.xalan.internal.xsltc.compiler.util.Util.println;

public class Test {


    public static void main(String[] args) {

        //创建测试顶点 假设已A为开始顶点
        Graphs.Vertex A = Graphs.Vertex.builder().id("A").content("A").isMaster(true).build();

        Graphs.Vertex B = Graphs.Vertex.builder().id("B").content("B").isMaster(false).build();

        Graphs.Vertex C = Graphs.Vertex.builder().id("C").content("C").isMaster(false).build();

        Graphs.Vertex D = Graphs.Vertex.builder().id("D").content("D").isMaster(false).build();

        Graphs.Vertex E = Graphs.Vertex.builder().id("E").content("E").isMaster(false).build();

        Graphs.Vertex F = Graphs.Vertex.builder().id("F").content("F").isMaster(false).build();

        Graphs.Vertex G = Graphs.Vertex.builder().id("G").content("G").isMaster(false).build();

        Graphs.Vertex H = Graphs.Vertex.builder().id("H").content("H").isMaster(false).build();

        Graphs.Vertex I = Graphs.Vertex.builder().id("I").content("I").isMaster(false).build();

        List<Graphs.Vertex> vertes = new ArrayList<>(9);

        vertes.add(A);vertes.add(B);vertes.add(C);vertes.add(D);
        vertes.add(E);vertes.add(F);vertes.add(G);vertes.add(H);
        vertes.add(I);

        List<Graphs.Edge> edges = new ArrayList<>(10);

        //这里我们定义了A-I共9个顶点 它们之间的关系为
        Graphs.Edge e1 = Graphs.Edge.builder().from("A").to("B").description("A与B之间的关系").build();

        Graphs.Edge e2 = Graphs.Edge.builder().from("A").to("C").description("A与C之间的关系").build();

        Graphs.Edge e3 = Graphs.Edge.builder().from("B").to("F").description("B与F之间的关系").build();

        Graphs.Edge e4 = Graphs.Edge.builder().from("C").to("D").description("C与D之间的关系").build();

        Graphs.Edge e5 = Graphs.Edge.builder().from("D").to("F").description("D与F之间的关系").build();

        Graphs.Edge e6 = Graphs.Edge.builder().from("D").to("E").description("D与E之间的关系").build();

        Graphs.Edge e7 = Graphs.Edge.builder().from("D").to("G").description("D与G之间的关系").build();

        Graphs.Edge e8 = Graphs.Edge.builder().from("E").to("H").description("E与H之间的关系").build();

        Graphs.Edge e9 = Graphs.Edge.builder().from("G").to("H").description("G与H之间的关系").build();

        Graphs.Edge e10 = Graphs.Edge.builder().from("H").to("I").description("H与I之间的关系").build();

        edges.add(e1);edges.add(e2);edges.add(e3);edges.add(e4);edges.add(e5);
        edges.add(e6);edges.add(e7);edges.add(e8);edges.add(e9);edges.add(e10);


        //被移除的顶点id
        String removeId = "D";

        //将边关系进行变更为map集合 k 为边中fromId List<V>为边实体
        Map<String,List<Graphs.Edge>> mEdges = new HashMap<>();

        //保存from顶点到关联集合顶点
        edges.forEach(edge->{

            //移除被删除顶点关联的边
           String toId =  edge.getTo();
           if(!removeId.equals(toId)){
               List<Graphs.Edge> edgs =  mEdges.get(edge.getFrom());
               if(edgs == null){
                   edgs = new ArrayList<>();
               }
               edgs.add(edge);

               mEdges.put(edge.getFrom(),edgs);
           }

        });


        //构建队列 这里使用java自带的LinkedList
        Queue<String> queue = new LinkedList<>();

        //访问过所有顶点 具有唯一性
        HashSet<String> wySet = new HashSet<>();

        //写入master 节点即开头顶点 唯一标示 从A开始遍历
        queue.add("A");
        wySet.add("A");

        while(!queue.isEmpty()){

            //获取当前点id
            String curId = queue.poll();

            //获取该顶点下一层关联所有顶点
            List<Graphs.Edge> relations = mEdges.get(curId);

            //代表为最后一层顶点
            if(relations == null) continue;

            for (Graphs.Edge edg : relations) {
                String nextId = edg.getTo();
                if (!wySet.contains(nextId)) {
                    queue.add(nextId);
                    wySet.add(nextId);
                }
            }
        }

        //去除不存在节点
        vertes = vertes.stream().filter(vertex -> wySet.contains(vertex.getId())).collect(Collectors.toList());

        //去除不存在的边
        edges = edges.stream().filter(edge ->     (wySet.contains(edge.getFrom()) && wySet.contains(edge.getTo()))).collect(Collectors.toList());


        //验证是否级连删除点 边
        vertes.stream().forEach(vertex -> println(vertex.getContent()));

        edges.stream().forEach(ed -> println(ed.getDescription()));

    }


}