最小生成--prime（普里姆）算法

普里姆最小生成树算法：

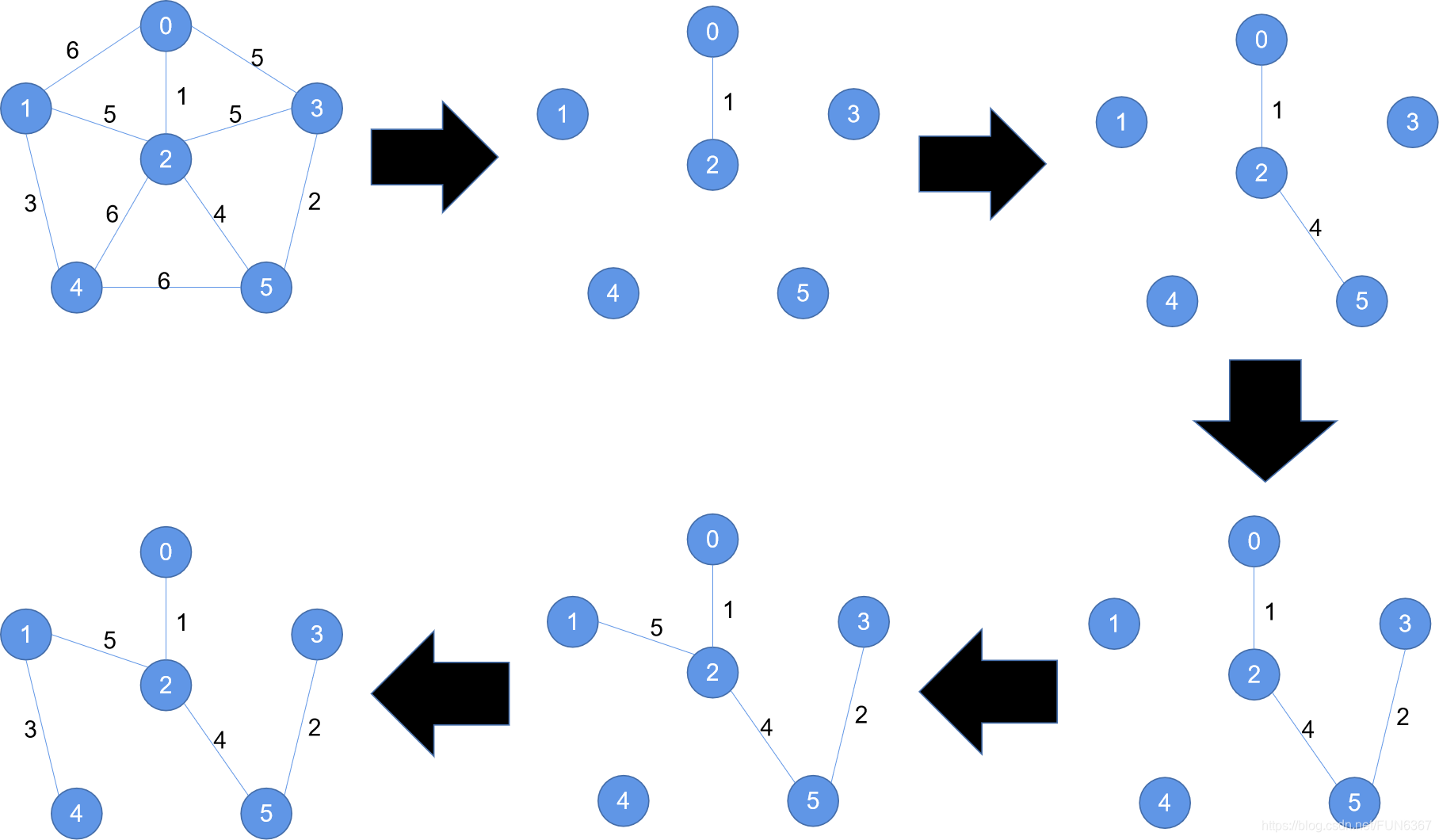
思想：贪心算法思想，以一个顶点为开始的最小生成树，不停选择到最小生成树权值最小的顶点并入，直到所有顶点并入

     

辅助数组：locast
存放还未并入最小生成树的顶点与最小生成树之间的最小权值的边（与lowcast数组共同作用）
  ex:lowcast[i] = 5 表示顶点i到最小生成树的最小权值为5
       lowcast[i] = 0 表示顶点i已并入最小生成树
       lowcast[i] = Max 表示顶点i与最小生成树之间还没有边连接

辅助数组：adjvex
存放还未并入最小生成树的顶点位于最小生树内的前驱（基于的边是lowcast数组中存放的最小权值边）
  ex:adjvex[i] = j; lowcast[i] = 5; 表示顶点i到最小生成树的最小权值为5的边j-i
       adjvex[i] = -1 时 lowcast[i] = Max

1.并入第一个顶点（随便），最为最开始的只有一个顶点的最小生成树

2.初始化lowcast， adjvex数组的数值

3.查找lowcast数组，选择最小权值的边

4.找到边后将相应的顶点并入

5.更新lowcast， adjvex数组并跳到第2.步直到所有顶点并入

总结过程为：查→并→更

代码：

#include <iostream>
#include<limits>
using namespace std;

typedef struct Graph{
    int vexnum, edgnum;
    int matrix[100][100];
    Graph(int v, int e):vexnum(v), edgnum(e){
        for(int i = 0; i < vexnum; i ++){
            for(int j = 0; j < vexnum; j ++){
                matrix[i][j] = INT_MAX;
            }
        }
    }
}Graph;

//初始化图
void initGraph(Graph &G){
    cout << "分别输入G的每条边的两个端点和权值（用空格隔开）：" << endl;
    int i, j, info;
    for(int k = 0; k < G.edgnum; k ++){
        cin >> i >> j >> info;
        if(i >= G.vexnum || i < 0 || j >= G.vexnum || j < 0){
            cout << "输入的顶点越界！" << endl;
            continue;
        }
        G.matrix[i][j] = info;
        G.matrix[j][i] = info;
    }
}

//输出图
void printGraph(Graph G){
    for(int i = 0; i < G.vexnum; i ++){
        for(int j = i; j < G.vexnum; j ++){
            if(G.matrix[i][j] < INT_MAX){
                cout << i  << "--" << j << ":" << G.matrix[i][j] << endl;
            }
        }
    }
}

/**
查找lowcast数组中的权值最小的边
返回值为lowcast数组的下标值
返回-1 表示最小生成树已并入所有顶点
**/
int findMinEdg(int *lowcast, int n){
    int minmum = Max;
    int tag = -1;
    for(int i = 0; i < n; i ++){
        if(lowcast[i] < minmum && lowcast[i] != 0){
            minmum = lowcast[i];
            tag = i;
        }
    }
    return tag;
}

int main()
{
    Graph G(6, 10);
    initGraph(G);
        /**
    辅助数组：locast
    存放还未并入最小生成树的顶点与最小生成树之间的最小权值的边（与lowcast数组共同作用）
    ex:lowcast[i] = 5 表示顶点i到最小生成树的最小权值为5
       lowcast[i] = 0 表示顶点i已并入最小生成树
       lowcast[i] = Max 表示顶点i与最小生成树之间还没有边连接
    **/
    int lowcast[G.vexnum];
    /**
    辅助数组：adjvex
    存放还未并入最小生成树的顶点位于最小生树内的前驱（基于的边是lowcast数组中存放的最小权值边）
    ex:adjvex[i] = j; lowcast[i] = 5; 表示顶点i到最小生成树的最小权值为5的边j-i
       adjvex[i] = -1 时 lowcast[i] = Max
    **/
    int adjvex[G.vexnum];
    /**开始将顶点0并入最小生成树**/
    lowcast[0] = 0;
    for(int i = 1; i < G.vexnum; i ++){
        lowcast[i] = G.matrix[0][i];
        if(lowcast[i] != Max){
            adjvex[i] = 0;
        }else{
            adjvex[i] = -1;
        }
    }
    /**初始化最小生成树**/
    Graph tree(G.vexnum, 0);
    for(int i = 0; i < tree.vexnum; i ++){
        for(int j = 0; j < tree.vexnum; j ++){
            tree.matrix[i][j] = Max;
        }
    }
    while(true){
        /**查找**/
        int j = findMinEdg(lowcast, G.vexnum);
        /**合并**/
        if(j != -1){
            tree.matrix[adjvex[j]][j] = G.matrix[adjvex[j]][j];  //无向边
            tree.matrix[j][adjvex[j]] = G.matrix[adjvex[j]][j];
        }else{
            break;
        }
        lowcast[j] = 0;
        tree.edgnum ++;
        /**更新**/
        for(int i = 0; i < tree.vexnum; i ++){
            if(lowcast[i] != 0){
                if(G.matrix[i][j] < lowcast[i]){
                    lowcast[i] = G.matrix[i][j];
                    adjvex[i] = j;
                }
            }
        }
    }
    /**输出**/
    cout << "最小生成树：" << endl;
    printGraph(tree);
    return 0;
}

运行结果：