【其他】【思考】目标检测与mAp(1)

最新推荐文章于 2025-03-13 08:37:40 发布

原创最新推荐文章于 2025-03-13 08:37:40 发布 · 523 阅读

0 ·

CC 4.0 BY-SA版权

其他专栏收录该内容

2 篇文章

订阅专栏

本文详细介绍了mAP（mean average precision）的计算方法，包括最常用的VOC2012中的mAP计算方式，并通过实例对比了不同检测器的效果，探讨了识别与定位准确性对mAP的影响。

一、mAp(mean average precision)

这一部分分析常见的mAp的计算方法。

首先来介绍最常用的mAp计算方法（VOC2012中所用到的）。

先做一个概述：

检测器对每一张图片进行检测，给出DR b-box
将所有图片的DR b-box集中，按照DR b-box给出的label进行分类
对于每个类别：
    将属于该类别的DR b-box按confidence降序排列。
    使用该类别的GT b-box去进行匹配（不重复）
    得到False Positive和True Positive
	接下来计算类Ci的Ap(average precision)
mAp = 所有类Ap的和 / 类的个数
得到mAp

以下为一个较为详细的伪代码：

检测器对每一张图片进行检测，给出DR b-box
将所有图片的DR b-box集中，按照DR b-box给出的label进行分类
for Ci in All Classes:
	N = 标签为Ci的GT b-box个数。
    记Di，为得到标签为Ci的DR b-box集合
	将按照confidence降序排列
	TP[size(Di)]=0
	FP[size(Di)]=0
    for d in Di:
		取得d所在的图像fig_d
		#接下来在fig_d中出现的GT b-box中匹配与d标签相同且IoU最大的GT
		max_IoU = 0
		best_match_GT = NULL
		for g in GT b-box:
			if g in fig_d:
				if label of g == label of d:
					if IoU(g, d) > max_IoU:
						best_match_GT = g
						max_IoU = IoU(g, d)
		#接下来计算FP，TP
		如果匹配best_match_GT不存在:
			FP[d] = 1
		如果匹配得到的max_IoU过小(<0.5)：
			FP[d] = 1
		如果匹配存在并且overlap够大：
			如果best_match_GT已经匹配过了：
				FP[d] = 1
			否则：
				TP[d] = 1
	#接下来计算类Ci的Ap(average precision)
	Prc_array[len(Di)]
	Rec_array[len(Di)]
	for k = 1 : 1 : len(Di):
		取Di中前k个为预测的正例，记为集合Pk
		精度Prc = Pk中的TP的数量 / k     #分子可以通过TP数组算出
		召回率Rec = Pk中TP的数量 / N
		Prc_array[k] = Prc
		Rec_array[k] = Rec
	根据Prc_array和Rec_array计算出Ap
	Ap = 根据Prc_array和Rec_array得到的PR曲线下的面积（积分）
	# Ap的计算方法有多种，在VOC2012中，就是先对PR曲线进行处理，使得它
	# 必定单调下降，之后再计算曲线下面积。
# 根据每个类的Ap计算出mAp(mean average precision)
mAp = 所有类Ap的和 / 类的个数
得到mAp。

可以看出来，mAp的计算将识别与定位的准确性同时考虑到了，它是以识别部分给出的confidence为基础（PR曲线绘制时使用的阈值就是confidence的阈值），结合定位给出的IoU来评估检测器的。其中涉及到的TP、FP概念在前一节中有所讨论。对于一个完美的检测器，其对于每一种类别，对于任意的Recall，Precision都是1，Ap就是1，最后mAp就是1。我们也可以提出一种以IoU为基础（PR曲线绘制时使用的阈值是IoU的阈值），结合识别的confidence来评估检测器的方法，流程与上面的mAp类似：

检测器对每一张图片进行检测，给出DR b-box
将所有图片的DR b-box集中，按照DR b-box给出的label进行分类
对于每个类别：
    在每张图片中使用GT b-box去进行匹配（不重复），得到对应GT b-box
    将属于该类别的DR b-box按匹配后与GT b-box的IoU值降序排列。
    得到False Positive（如果标签不一致或者confidence过小）和True Positive
	接下来计算类Ci的Ap(average precision)
mAp = 所有类Ap的和 / 类的个数
得到mAp

两者的出发点稍有区别，但是对于TP和FP的观点是一致的，至于说哪个好，还需要更详细的分析。（对于样本个数、类别均衡度的鲁棒性分析需要）

我们假设两种较为极端的检测器，将空间感知能力以及识别能力分开考虑。另外考虑分类器分的过多和过少的情况。

第一种检测器Dtn1，它对于位置的感知极为准确，但是它的分类能力一般，总体上只能有50%的可能性分对。我们考虑两种算法的Ap。

第一种算法，对于任意的confidence阈值，在前面都有大约一半的TP，因此Precision为0.5，最大的召回率为0.5，而FP只由分类错误产生，因此最终有0.25的Ap。假设检测器有m的可能性分对，则Ap为m^2（样本非常多的情况下）。

第二种算法，IoU阈值在这里失去了作用，对于任意的IoU阈值，前面都有大约一半分错，由于confidence过小的也会筛除掉，因此会更少一些，最大的召回率是一样的，Ap会略小于0.25。假设有m的可能性分对，则Ap为m^2。

第二种检测器Dtn2，它对于位置的感知一般，平均的与GT的IoU为0.5，但是分类能力极好，只要有一小部分的GT与其重合，那么它就能分类出来。

二、其他的一些讨论

https://zhuanlan.zhihu.com/p/56899189

具体计算一些这里面的一些例子，来更深刻的理解mAP

preview

结果是：

preview preview

下面来计算一下为什么是这样：

mAP一共取了0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95共10个阈值。

在mAP0.5处，Recall最多为0.33，精度为1，所以mAP均为0.33。至于为什么是0.337，在回答中有所解释：直观来看Recall最大为0.33，所以0-0.33期间Precision都为1。那么计算下来mAP应该等于0.33才对。但是实际上COCO计算mAP时使用了recall = [0, 0.01, ..., 1.00]共101个采样点，因此共有34（0到0.33）个点的Precision=1，其余均为0。所以其mAP为 34/101 约等于0.337。

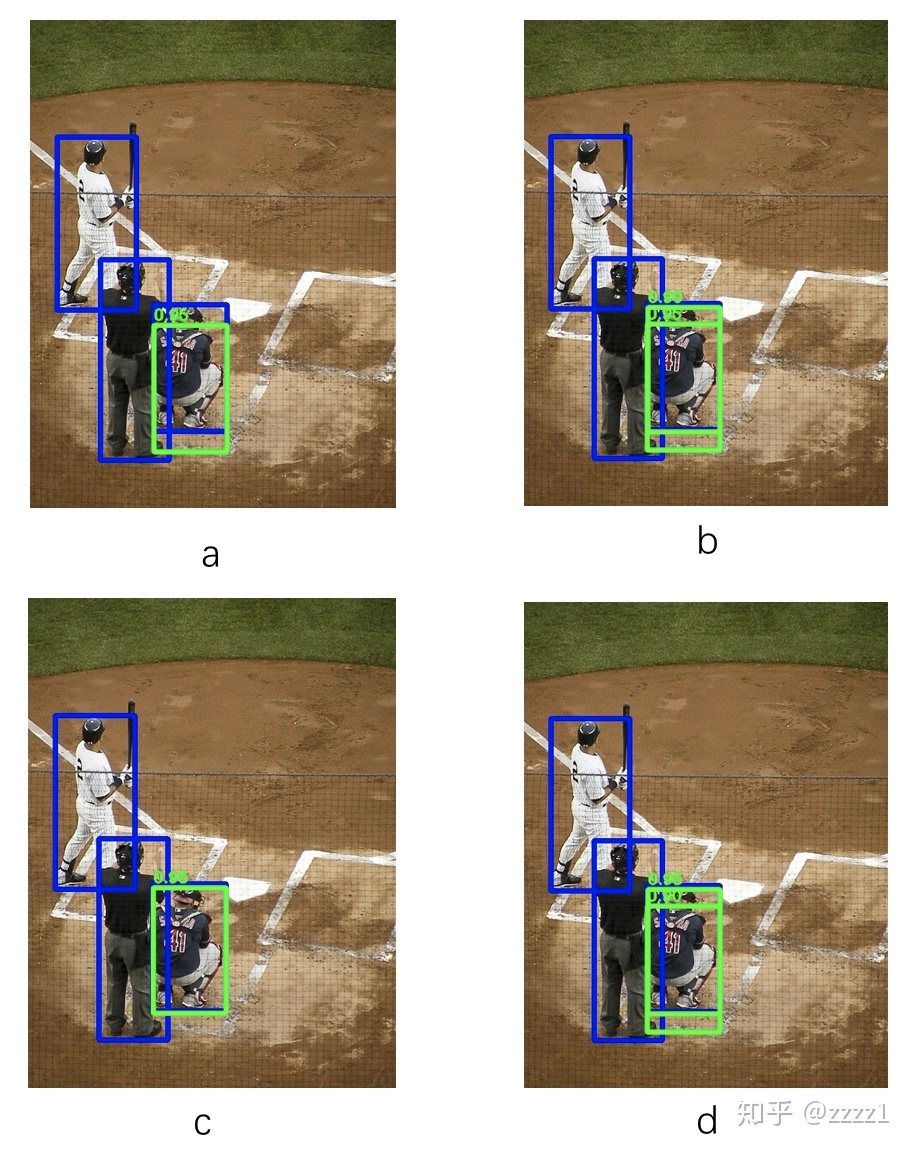
在mAP0.75处：

A：没有匹配，mAP=0

B：0.96的DT是FP，0.90的DT是TP，此时Recall达到0.337，Precision为0.5，mAP=0.337 * 0.5 = 0.168

C：匹配上，mAP=0.337

D：0.96的DT是TP，此时Recall=0.337，Precision为1。之后的DT是FP，Precision=0.5。但由于相同Recall下，Precision取最大值，Precision=1，mAP=0.337 * 1 = 0.337