【MATLAB】【公式验证】傅里叶级数

原创已于 2022-04-14 11:23:13 修改 · 5.2k 阅读

38 ·

CC 4.0 BY-SA版权

文章标签：

#matlab

于 2022-04-14 11:21:28 首次发布

信号与系统同时被 2 个专栏收录

5 篇文章

订阅专栏

基于MATLAB的数学公式验证

2 篇文章

订阅专栏

本文通过Matlab实例展示了傅里叶级数在信号处理中的应用，对比不同项数的拟合效果，探讨高频噪声对拟合质量的影响，并提示后续深入学习的解决策略。

傅里叶级数

关于傅里叶级数的概念和工程意义在这不再叙述，此文章只是用matlab把图形拟合出来，让读者形象地感受随着项数的增加，函数拟合效果逐渐逼近。
以下为傅里叶级数的总体概况：
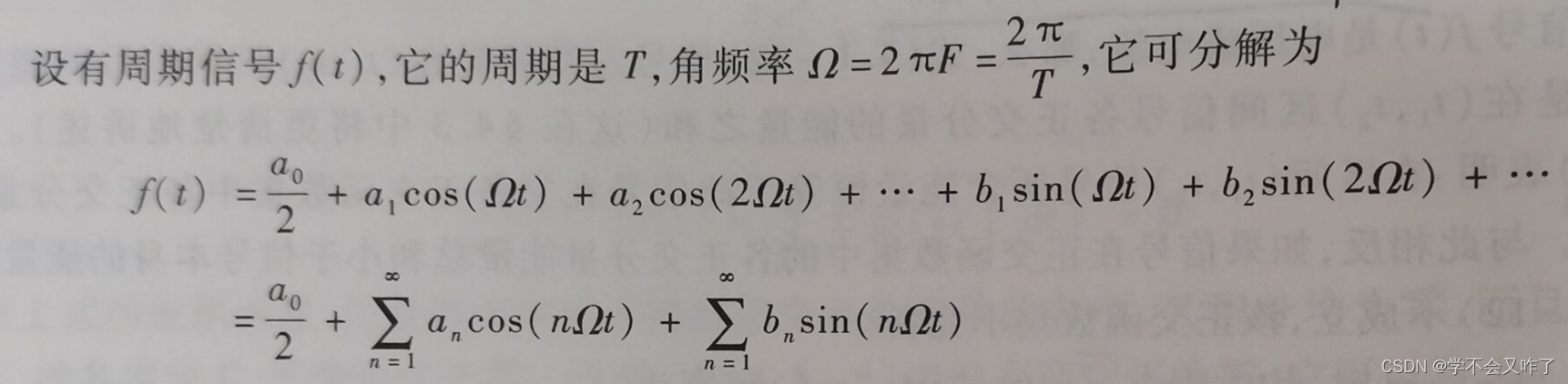
在这里插入图片描述
傅里叶系数的求解：

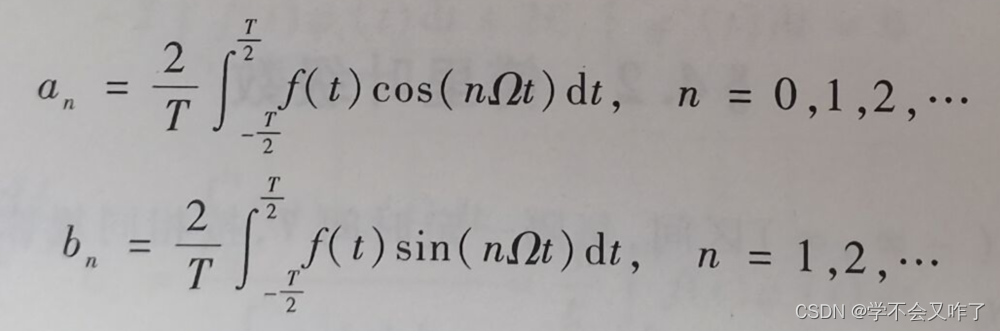
方波信号的傅里叶级数

对以下信号进行傅里叶级数展开：
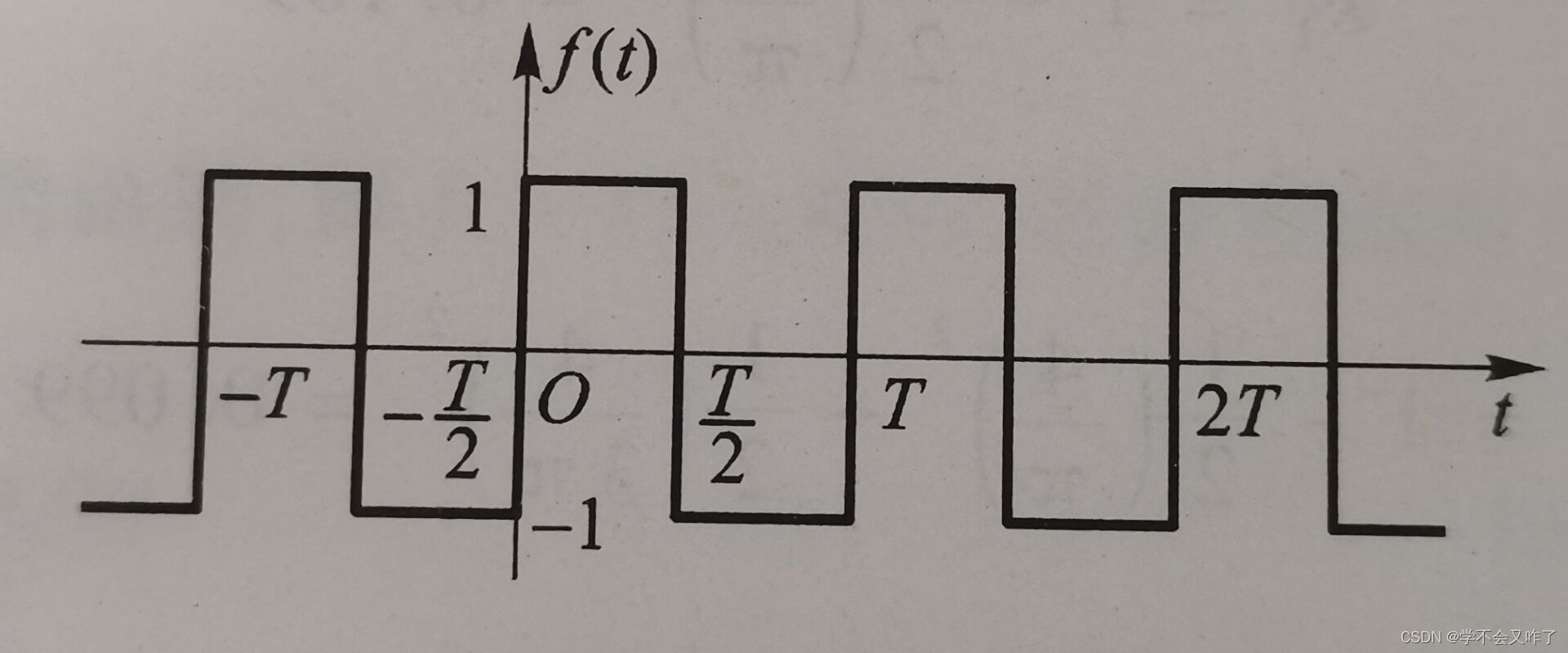
请添加图片描述
根据傅里叶级数展开公式得此信号的傅里叶展开为：
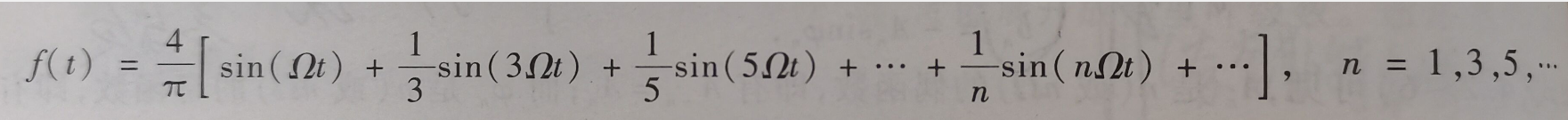
在这里插入图片描述

其中周期T取2。
三项拟合：

t=-2:0.01:2;
f1=square(pi*t);
f2=4/pi*(sin(pi*t)+sin(3*pi*t)/3+sin(5*pi*t)/5);
plot(t,f1,t,f2);
xlabel('x')
ylabel('y')

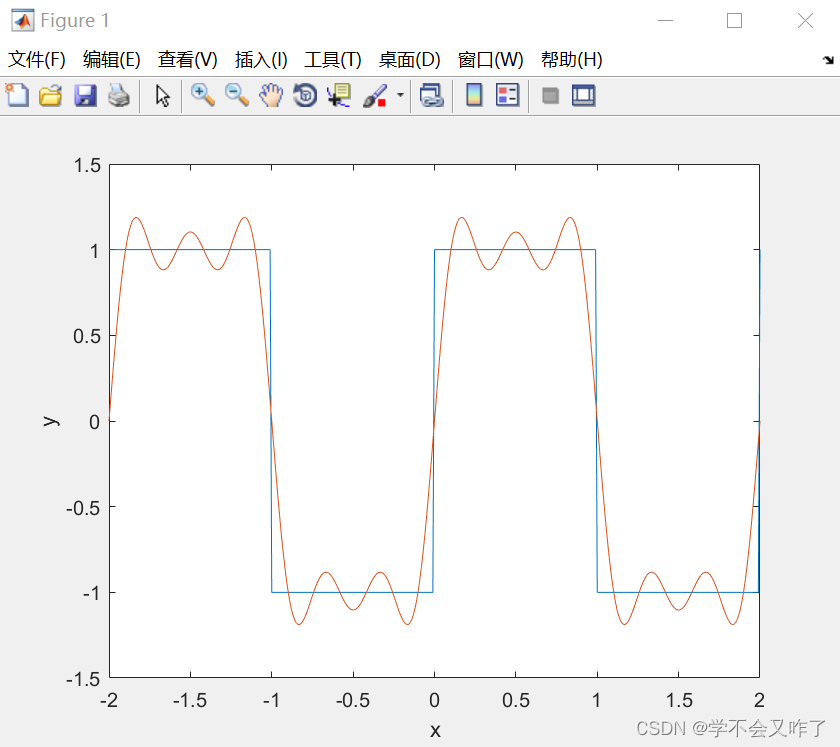
在这里插入图片描述
五项拟合：

t=-2:0.01:2;
f1=square(pi*t);
f2=4/pi*(sin(pi*t)+sin(3*pi*t)/3+sin(5*pi*t)/5+sin(7*pi*t)/7+sin(9*pi*t)/9);
plot(t,f1,t,f2);
xlabel('x')
ylabel('y')

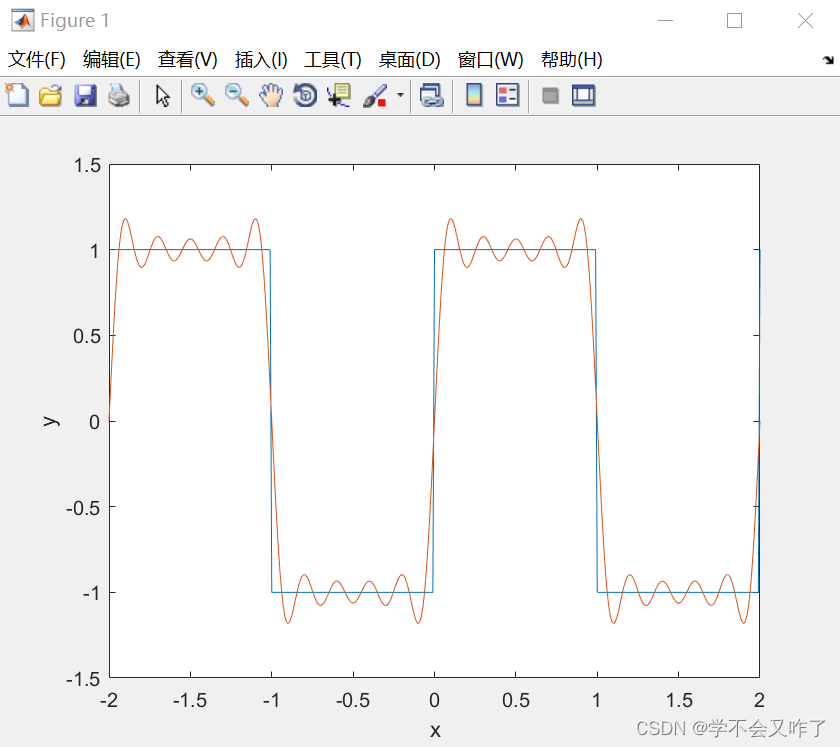
在这里插入图片描述
十项拟合：

t=-2:0.01:2;
f1=square(pi*t);
f2=4/pi*(sin(pi*t)+sin(3*pi*t)/3+sin(5*pi*t)/5+sin(7*pi*t)/7+sin(9*pi*t)/9+sin(11*pi*t)/11+sin(13*pi*t)/13+sin(15*pi*t)/15+sin(17*pi*t)/17+sin(19*pi*t)/19);
plot(t,f1,t,f2);
xlabel('x')
ylabel('y')

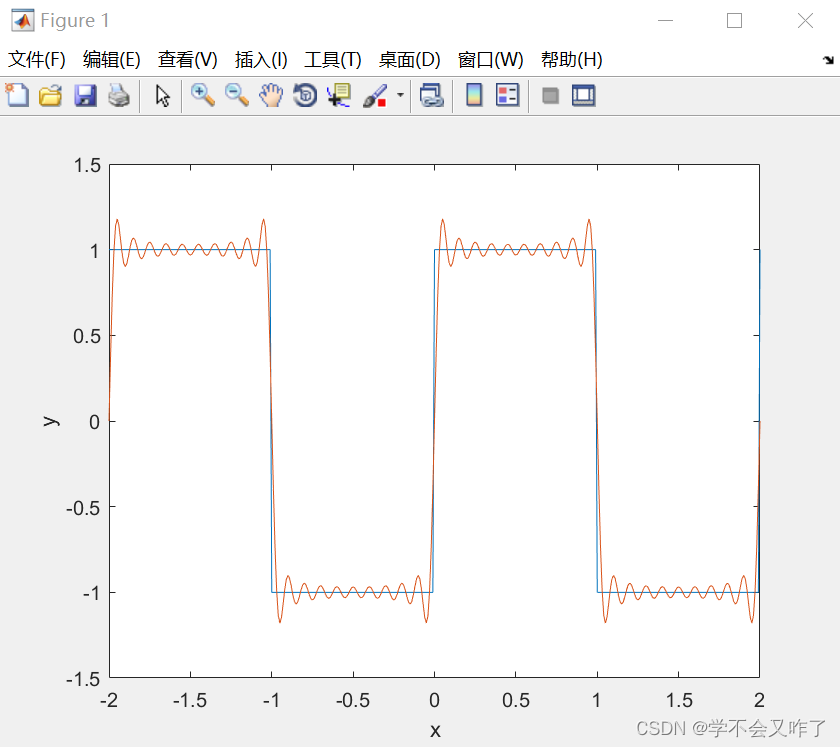
在这里插入图片描述

总结

随着项数的增加，两曲线逐步逼近，但随着项数的增加（高频信号，因为nw逐渐增加）导致信号的边沿部分出现毛刺，如何解决此问题待我深入学习后再来更新解决方案。