寻找峰值

目录

​​​​​​一：题目链接

二：题目思路

三：代码实现

---

​​​​​​一：题目链接

二：题目思路

首先，题目会出现三种情况。

        情况1：数组元素随着下标增加一直增大，也就是 “直线往上” ，题目结果就是返回数组最后一个元素位置。

        情况2：数组元素随着下标增加一直减小，也就是 “直线往下” ，题目结果就是返回数组第一个元素位置。

        情况3：数组元素大小变化不固定，也就是 “起伏不平”，此时，可以这样分析，如图：

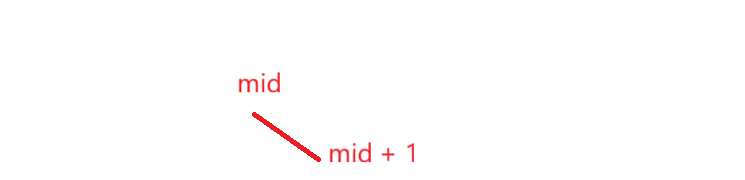
        mid 是对应元素位置，线的高低表示当前位置元素的大小，此时可以说明 mid 左边（包括 mid）一定会有峰值。此时 mid 右边的就不用管了。同理，另一种起伏如下图：

      此时可以说明 mid 右边一定会有峰值。此时 mid 左边的就不用管了。

       到这里，我们发现了其 “二段性” ，就可以使用 二分查找 算法来解决了。

三：代码实现

        int left = 0;
        int right = nums.length - 1;

        while(left < right) {
            int mid = left + (right - left) / 2;

            if(nums[mid] < nums[mid + 1]) {
                left = mid + 1;
            }else {
                right = mid;
            }
        }

        return left;