二叉树的性质和分类

目录

原文章：

说在前头：

二叉树的性质：

(1).二叉树的第i层上面最多有 2i−1 个结点(i >= 1)：

(2).深度为k的二叉树最多有 2k−1 个结点( k >= 1 )。

(3).对任一棵二叉树，如果其终端结点（叶子）数为 n0 ，度为2的结点数为 n2 ，则n0＝n2＋1。

(4).具有n个结点的完全二叉树的深度为 ⌊log2n⌋+1 。

二叉树的分类：

(4).具有n个结点的完全二叉树的深度为⌊log2n⌋+1 ：

感兴趣的话可以关注完整内容：

---

原文章：

二叉树的性质和分类 - 知乎

此文章为作者本人搬运至该网站。

---

说在前头：

这里的内容是我的这个文章的节选：

数据结构学习记录：第六章：树和二叉树-优快云博客

因为这一篇文章内容实在太多，可能导致有些重要内容各位看不到，所以我就把我认为的重要内容给单独开出来。

---

二叉树的性质：

最有重量级的一集！

二叉树，顾名思义，就是每个结点最多只有两个孩子的树，而二叉树有以下5种基本形态：

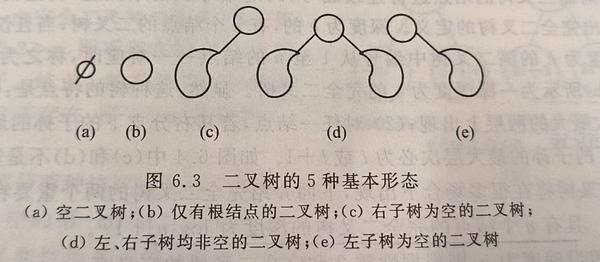
图中结点的表示为圆圈，而叶子表示为近似半个八卦形状，但是其实两者从实际意义上来说也没有什么区别。

这里是几个知识点，考试的时候可能会出填空题选择题之类的。

---

(1).二叉树的第i层上面最多有 2i−1 个结点(i >= 1)：

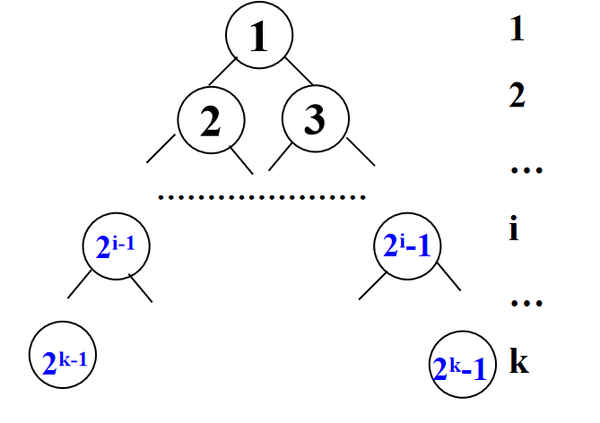
解释：如这个图所示，第1层的结点是1个， 20=1 ，

第2层的结点，由第1层的结点分成2个，共有2个， 21=2 ，

第3层的结点，由第2层的每个结点分别再分成2个，共有4个， 22=4 ，

以此类推。。。

---

(2).深度为k的二叉树最多有 2k−1 个结点( k >= 1 )。

解释：如果把二叉树的每个结点都写上数字，如上图，从左到右，从上到下，那么到k层的时候，最右边的结点的数字就是 2k−1 ，

第1层只有一个结点，最右边也就是那一个结点，数字为 21−1=1 ，

第2层，最右边结点数字为 22−1=4−1=3 ，

第3层，最右边结点数字为 23−1=8−1=7 ，

以此类推。。。。

同时要注意！！！这一层最左边的结点数字是 2k−1 ！！！最右边的是2k−1，两者看似相像却又相隔甚远，一定不要写错了！！

如果记不住的话，可以自己写一遍二叉树，最左边的结点数字和最右边的结点数字就会清晰许多。

---

(3).对任一棵二叉树，如果其终端结点（叶子）数为 n0 ，度为2的结点数为 n2 ，则n0＝n2＋1。

解释：终端结点（叶子结点），也就是没有孩子的结点，而度为2的结点，其实就是有两个孩子的结点，也就是说，没有孩子的结点的数目，就是有两个孩子结点的数目再加上1。

---

(4).具有n个结点的完全二叉树的深度为 ⌊log2n⌋+1 。

注意！！！在这里出现了一个新名词：完全二叉树。

那这个第四点我们就按下不表，先去讲一下二叉树的种类。

---

二叉树的分类：

二叉树分为：满二叉树、完全二叉树和非完全二叉树（注意，这里的界限并不是完全分明的）

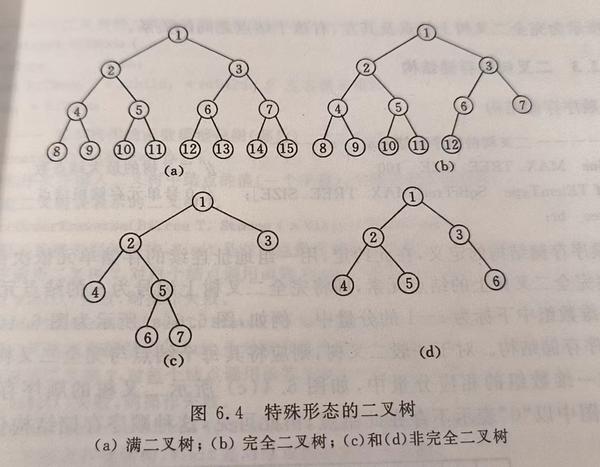
满二叉树：顾名思义，每个结点不是终端结点（叶子结点）就是有两个孩子的结点，整个二叉树的图看起来极其完美。

完全二叉树：其实如果光听名字的话，满二叉树和完全二叉树确实很容易混淆。大家还记得在上面讲二叉树的性质的内容我们是怎么讲的吗？

就是把每个结点都用一个数字标记，从上到下，从左到右依次递增，那么这样如果在数组里面存的话，就是从0递增，每个数字都有结点相对应，

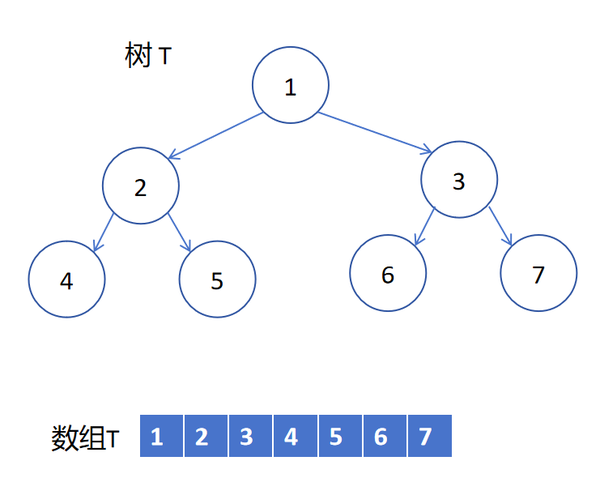
满二叉树，也是完全二叉树

（注意！！！这里我犯了个不明显的错误！！！树的图形表示里面，两个结点之间的连线是没有箭头的！！！我先入为主地给加上了后面也有很多有箭头的连线，大家注意！！！课本里面以及很多网上教程都是不带箭头的！！！）

这里不把数组第一个写成0是因为要和树的形式对齐。

但是当我们去掉6和4的时候，由于顺序都是从上到下，从左到右，那么这样数组就只能这样写：

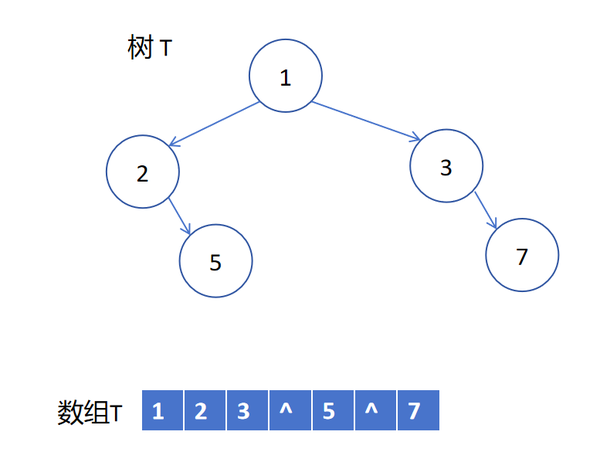
这样就不是完全二叉树了，而叫做非完全二叉树。

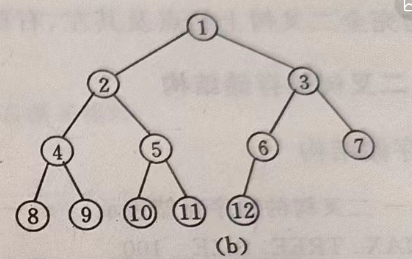
也就是说，完全二叉树，必须要保证每个结点都是从左到右连续的，比如之前图中图b的样子：

还有这些，也是完全二叉树：

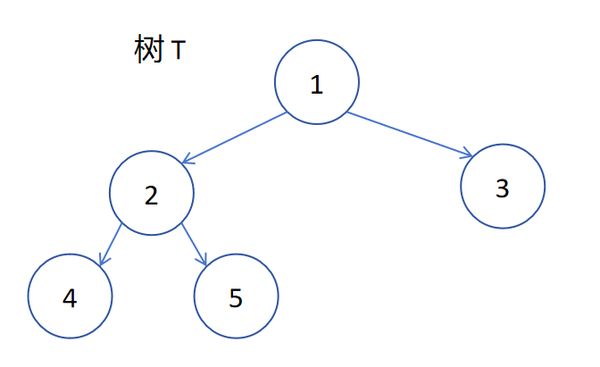
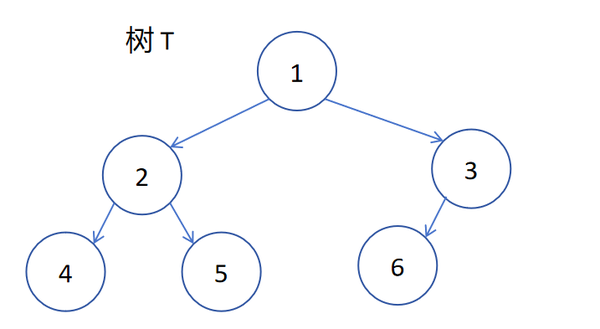
而以下的这些都是非完全二叉树（红色方框表示导致其为非完全二叉树的部分）：

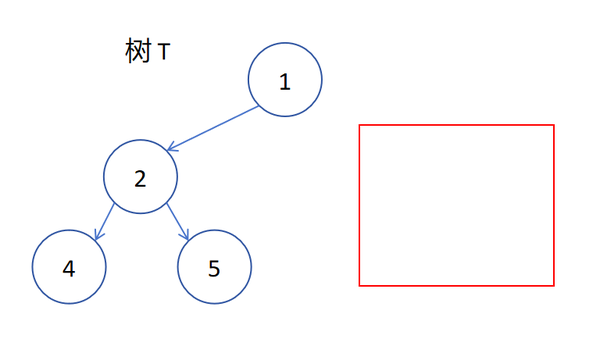
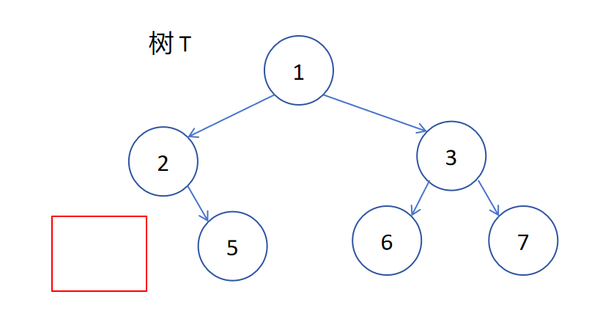
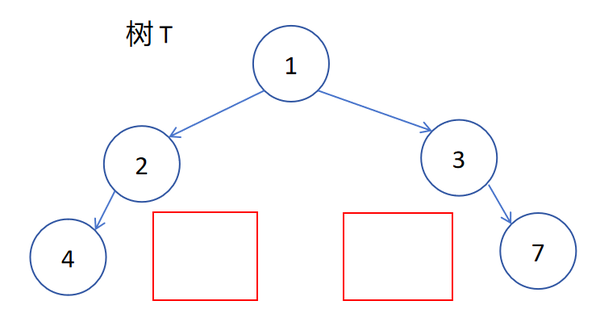
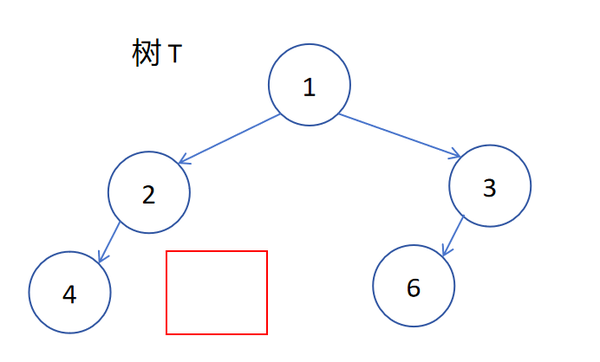
这里最右边的那个结点缺失并不是该树成为非完全二叉树的原因

这样是不是比较清晰了？

同时要记得，一个树，不是完全二叉树就是非完全二叉树，

而满二叉树，满足完全二叉树的所有要求，那么它其实就是完全二叉树的一个特殊情况~

了解了完全二叉树后，我们再回来看那个二叉树的性质：

(4).具有n个结点的完全二叉树的深度为⌊log2n⌋+1 ：

大家别觉得有个log就是多么神奇的东西了，简单回想一下， log2n 是什么意思？

忘了？那么 log22 呢？

其实就是求这个数是2的几次方。（我知道可能会有很多人觉得这个log还要讲？虽然但是，我是真的第一眼没看出来TAT）

还有一点就是，括住 log2n 的括号其实没有上面那一横！！！

不过还好课本已经给出了这个⌊x⌋负号的运算：

表示不大于x的最大整数。

而如果去掉下面一横

⌊x⌋

那就是表示不小于x的最小整数。

我们就这个满二叉树为例：

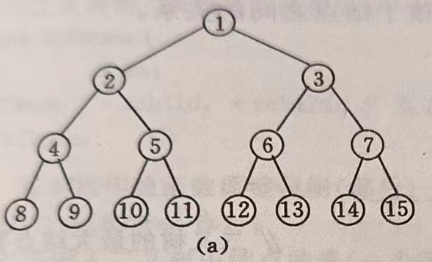
(4).具有n个结点的完全二叉树的深度为⌊log2n⌋+1 。

这里n为15，那么

⌊log28⌋=3<⌊log215⌋<⌊log216⌋=4

深度就是3+1=4，符合题目情况，

而如果是图b里面的完全二叉树，公式也是一样的，这里不过多细究。

---

感兴趣的话可以关注完整内容：

数据结构学习记录：第六章：树和二叉树-优快云博客