目录
1.memset所初始化的数组若为int类型,则只能赋值为-1或0,赋其他值时会出现错误:
2.memset的若为char类型,则可以为任意值,但是赋值的数字为ASCII的值:
原文章:
此文章为作者本人搬运至该网站。
所学习文章:
在此向原作者表示感谢!!!
本来想先学一下map和set再来开这章的,不过set的内容除了复制粘贴感觉没什么可以讲的,并且还有一点就是:如果不做题的话,再怎么讲怎么复制粘贴都没啥用。
所以在这篇文章之后,我也该着手开始刷题了,第一个目标就是蓝桥杯!
一、accumulate——求和函数:
accumulate(beg, end, init)
其中init为求和的初始值,即最终结果为 init的数值+beg的位置的数值直至end的位置的数值的和。
#include <bits/stdc++.h>
using namespace std;
int main(){
vector<int> a{1, 2, 3, 4, 5};
int b = accumulate(a.begin(), a.end(), 0);
cout << b << endl;
//对于vector的a,从首位置到末位置求和,初始值为0,结果为:15
int a2[] = {1, 1, 1, 1, 1};
int b2 = accumulate(a2, a2 + 3, 10);
cout << b2;
//对于数组的a2,从首位置到首位置后面三位 的区间求和,初始值为10,结果为 13
return 0;
}
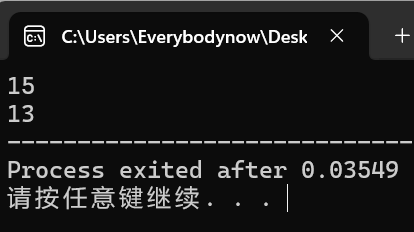
beg和end理所当然为迭代器。
反正就经验来看,对于使用vector的任意函数,操作里面的元素都要用到begin()和end(),而如果是普通数组就只需要数组名了。
二、atoi——字符串转int类型の函数:
string s = "1234";
int a = atoi(s.c_str());
printf("%d", a);
char s[] = "1234";
int a = atoi(s);
cout << a << "\n";
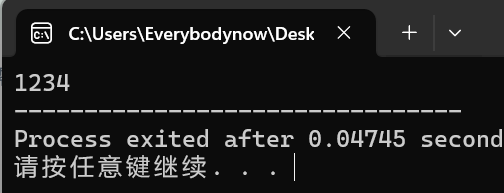
感觉没什么多说的。
三、fill和memset——初始化赋值函数:
我最开始学习的初始化数组时所用的就是memset,不过如今才发现其有诸多限制,如:
1.memset所初始化的数组若为int类型,则只能赋值为-1或0,赋其他值时会出现错误:
int a2[5];
memset(a2, 0, sizeof(a2));
for(int i = 0; i < 5; i++)
cout << a2[i] << " ";
cout << endl;
memset(a2, -1, sizeof(a2));
for(int i = 0; i < 5; i++)
cout << a2[i] << " ";
cout << endl;
memset(a2, 1, sizeof(a2));
for(int i = 0; i < 5; i++)
cout << a2[i] << " ";
cout << endl;
比如这里,我定义了一个长度为5的普通数组a2,分别用memset赋值为0,-1,1:
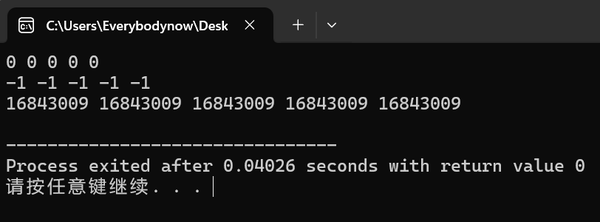
在赋值为1的时候会出现乱码,其余赋值,如-2,2也是一样的乱码。
原因似乎挺复杂,咱就不用了解了。
2.memset的若为char类型,则可以为任意值,但是赋值的数字为ASCII的值:
char a2[5];
memset(a2, 1, sizeof(a2));
for(int i = 0; i < 5; i++)
cout << a2[i] << " ";
cout << endl;
memset(a2, '1', sizeof(a2));
for(int i = 0; i < 5; i++)
cout << a2[i] << " ";
cout << endl;
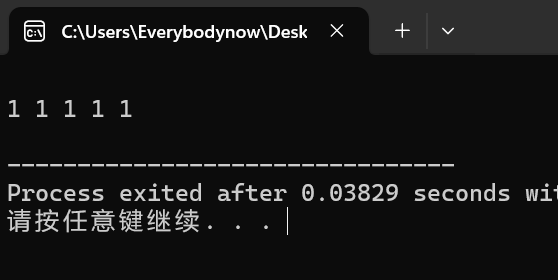
这里第一行看似没有输出,其实输出的是ASCII码值为1的字符,也就是空白字符。
而下面那个,就是把memset中的1换成了'1',其实就是1字符对应的ASCII码值,如果把'1'换成49,那么结果也一样。
而memset不仅有以上两个限制,还有:
C++踩坑——用memset对vector进行初始化 - Peyton_Li - 博客园
memset似乎不支持vector类型的数组。。。。。
所以还是建议不使用memset了。
3.fill:
fill(beg, end, num)
//对a数组的所有元素赋1
int a[5];
fill(a, a + 5, 1);
for(int i = 0; i < 5; i++)
cout << a[i] << " ";
cout << endl;
//1 1 1 1 1
vector<int> b(5);
fill(b.begin(), b.end(), 5);
for(int i = 0; i < 5; i++)
cout << b[i] << " ";
cout << endl;
//5 5 5 5 5
fill的使用格式和上面的acculamtate,就不多讲了。
四、lower_bound 和 upper_bound:
关于lower_bound( )和upper_bound( )的常见用法_lowerbound和upperbound-优快云博客
这两个函数的目的是在某一序列中 查找 第一个比一个指定元素大或者小的位置。
而其原理也就是二分查找,故而可以用于需要二分查找的题目。
1.先讲lower_bound普通数组的:
int a[] = {1, 2, 3, 4, 5};
cout << *(lower_bound(a, a + 5, 3)) << endl;
lower_bound是在a数组中查找第一个大于等于3的元素,并返回该元素的地址,
由于返回的是地址,所以我们要输出内容就先要加个星号(*),
上面输出的结果是3,我就不赘述了。
而如果把上面代码换成这个:
int a[] = {1, 2, 3, 4, 5};
cout << *(lower_bound(a, a + 2, 4)) << endl;
lower_bound函数中,a指的是1,a+2指的就是3,在1到3里面找不到4这个元素,那么!
这里有个很让人脑阔疼的原理:
我们先回归lower_bound的一般式:
lower_bound( begin, end, num);
这里要看好:
lower_bound的原理是:
从数组的begin位置到end - 1位置(包括这俩)进行查找第一个大于等于num的元素,
也就是说,查找区间的右端其实是end-1(end函数的老毛病。。。),但是函数里面写的还是end,然后,
如果找不到的话,那就返回end,
我们结合那个例子来看:(我把代码搬下来了)
int a[] = {1, 2, 3, 4, 5};
cout << *(lower_bound(a, a + 2, 4)) << endl;
这里查找范围是a到a+2,也就是从1到3,查找不到比4大的数,那么就返回end下标。
在这里,end 就等于 a + 2,也就是3,最后输出的结果就是3。
这一点感觉还是挺绕的。。。
2.接着就是vector数组的:
vector<int> b{1, 2, 3, 4, 5};
cout << *(lower_bound(b.begin(), b.end(), 4)) << endl;
其实vector的lower_bound和上面的类似,不过还是一如既往的用到begin和end,
(在这里别忘了end其实指的是数组最后一位 再往后一位的 这一位,也就是为什么上面要有end - 1了)
upper_bound也类似,只要记得lower是找第一个大于等于指定元素的位置,
而upper是找第一个小于等于的。
3.可以直接用作数组下标:
这个题,就是典型的二分查找的题,当然也可以用lower_bound做出来,
lower_bound要找的是第一个小于这个元素的位置,那么也正好规避了这个元素在数组里面重复的情况。
毕竟找到小于这个元素的话,那么往右挪一格不就是第一次出现这个元素了吗?
另外就是,lower_bound输出的是这个数的位置的地址,但是如果我们再直接减去这个数组(相当于减去它的首地址),地址减去地址,最后得出来的不就是这个数在数组中的位置了吗!!!
附上AC代码:
#include <bits/stdc++.h>
using namespace std;
int arr[1000005];
int main() {
int n, m;
cin >> n >> m;
for (int i = 0; i < n; i++) {
cin >> arr[i];
}
int qus; //要找的数字
for (int i = 0; i < m; i++) {
cin >> qus;
int ans = lower_bound(arr, arr + n, qus) - arr; //这个是最核心之处
//找出第一个比qus小的数的位置
if (arr[ans] != qus) cout << "-1 ";
else cout << ans + 1 << " ";
}
return 0;
}
五、max_element 和 min_element:
在区间内找最大最小值,应该不用多说,看代码就行:
int a[] = {1, 2, 3, 4, 5};
int mx = *max_element(a, a + 3);
cout << mx << endl;
//输出结果:3
vector<int> a2{1, 2, 114514, 4, 5};
int mx2 = *max_element(a2.begin(), a2.end());
cout << mx2;
//输出结果:114514
六、max 和 min:
找多个元素的最大值最小值:
//找a,b的最大值和最小值
mx = max(a, b);
mn = min(a, b);
//找到a,b,c,d的最大值和最小值
mx = max({a, b, c, d});
mn = min({a, b, c, d});
mx = max({1, 2, 114514, 3});
//结果:114514
pass。
七、reverse:
反转某个数组或字符串,可以用来判断回文串啥的:
reverse(beg,end);
string s = "abcde";
reverse(s.begin(), s.end());//对s进行翻转
cout << s << '\n';//edcba
//对a数组进行翻转
int a[] = {1, 2, 3, 4};
reverse(a, a + 4);
cout << a[0] << a[1] << a[2] << a[3];
//4321
八、sort:
最重量级的一个!
sort简单排序我就不讲了,想看的话可以看一下我前面的文章:
从C语言到C++/STL(二):vector动态数组-优快云博客
在这里讲一下一个新东西:更换排序规则
也就是原先是从小到大排序的,
//对a数组的[0, n-1]位置从大到小排序
sort(a, a + n, greater<int>());
//对a数组的[0, n-1]位置从小到大排序
sort(a, a + n, less<int>());
vector<int> b(n + 1);
sort(b.begin() + 1, b.end()); // 升序
sort(b.begin() + 1, b.end(), greater<int>()); // 降序
在下面这里就实现了从大到小排序。
另外,根据数组结构体里面的某个元素对所有结构体进行排序:
间隔这么长时间,我才发现我还有个sort的问题没解决:
那就是sort不能直接对存放结构体的数组进行排序啊!
原因毕竟很简单,结构体内部有多个元素,如果不指定是哪个元素,那么又如何排序呢?
因此需要如下代码:
struct node {
elemtype x;
}node[N];
// 1. 使用函数自定义排序,定义比较函数
bool cmp(node a, node b) {
//按结构体里面的x值降序排列
return a.x > b.x;
}
sort(node, node + n, cmp); // 只能接受 以函数为形式的自定义排序规则,无法接受以结构体为形式的自定义排序规则
// 2. 或者使用匿名函数自定义排序规则
sort(node, node + n, [](node a, node b) {
return a.x > b.x;
});
这个我建议用上面哪个,毕竟好记嘛。
在这里面,a.x就成为了结构体中的某个元素。
就通过这个元素对数组中所有的结构体进行排序。
九、nth_element:
STL 之 nth_element详解_nthelement-优快云博客
一句话解释:找出某区间第k(位置)小的数值。
用法:nth_element(a,a+k,a+n),k为所求的位置,n为右边界。
但是要注意的是!函数只是把下标为k的元素放在了正确位置,对其它元素并没有排序,
不过可以确定的是,k左边元素都小于等于它,右边元素都大于等于它,所以可以利用这个函数快速定位某个元素。
#include<bits/stdc++.h>
using namespace std;
int main() {
int a[9] = {4,7,6,9,1,8,2,3,5};
nth_element(a, a + 2, a + 9);
//将下标为2,也就是第3个数放在正确的位置
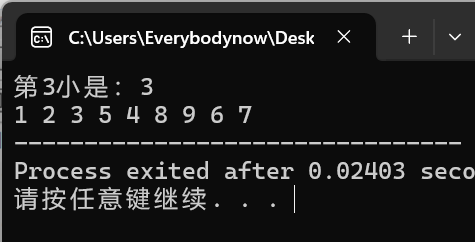
//也就是求的是第3小
cout <<"第3小是:"<< a[2] << endl;
//输出调整后的数组
for(int i = 0; i < 9; i++)
cout << a[i] << " ";
return 0;
}
十、find查找:
[C++] 基础教程 - std::find函数介绍和使用场景-优快云博客
c++STL中的find()函数 有两种使用方法_stl find函数返回值-优快云博客
原先我以为find只在string有,如今才发现vector,queue,甚至一般的数组都能用!
find返回的是一个迭代器,用法就是find (a.begin(), a.end(), x),
不过需要说明的是,vector似乎不能直接用 int *it 的指针来指向,要么用auto,要么用迭代器指针:
C++ find()函数用法(一般用于vector的查找)_c++ vector find-优快云博客
而对于普通数组,则是可以用int *it 的:
int res[5] = { 0,1,2,3,4 };
int *pos = find(res, res + 5, 5);
//这里的查找范围是指针
//res+5不在查找范围内
if (pos == (res + 5))
cout << "Couldn't find it";
else
cout << "Find it!";
其他可以看上面那几个文章。
十一、__gcd()求最大公约数:
我都没想到连求最大公约数都有方便函数!!!
用法很简单:
int answer = __gcd(a, b); //注意是两个下划线
//__gcd(12,15) = 3
//__gcd(21,0) = 21
然后没了,
就这么简单!!!
另外,求了最大公约数就一定绕不开最小公倍数:
求法就是用两个数相乘再除以这个最大公约数:
int mingbs = (a * b) / __gcd(a, b);
其他基本上要么比较复杂要么目前还没用上,先不讲了。























 1765
1765

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








