蓝桥杯真题洛谷U410524 埃及分数题解

 题目描述

**本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可**

古埃及曾经创造出灿烂的人类文明，他们的分数表示却很令人不解。古埃及喜欢把一个分类分解为类似: 1/a + 1/ b 的格式

这里，a和b必须是不同的两个整数，分子必须为1。
比如，2/15 一共有 4种不同的分解法(姑且称为埃及分解法):

1/8 + 1/120

1/9 + 1/45

1/10+1/30

1/12 + 1/20

那么，2/45 一共有多少个不同的埃及分解呢(满足加法交换律的算同种分解)?

思路

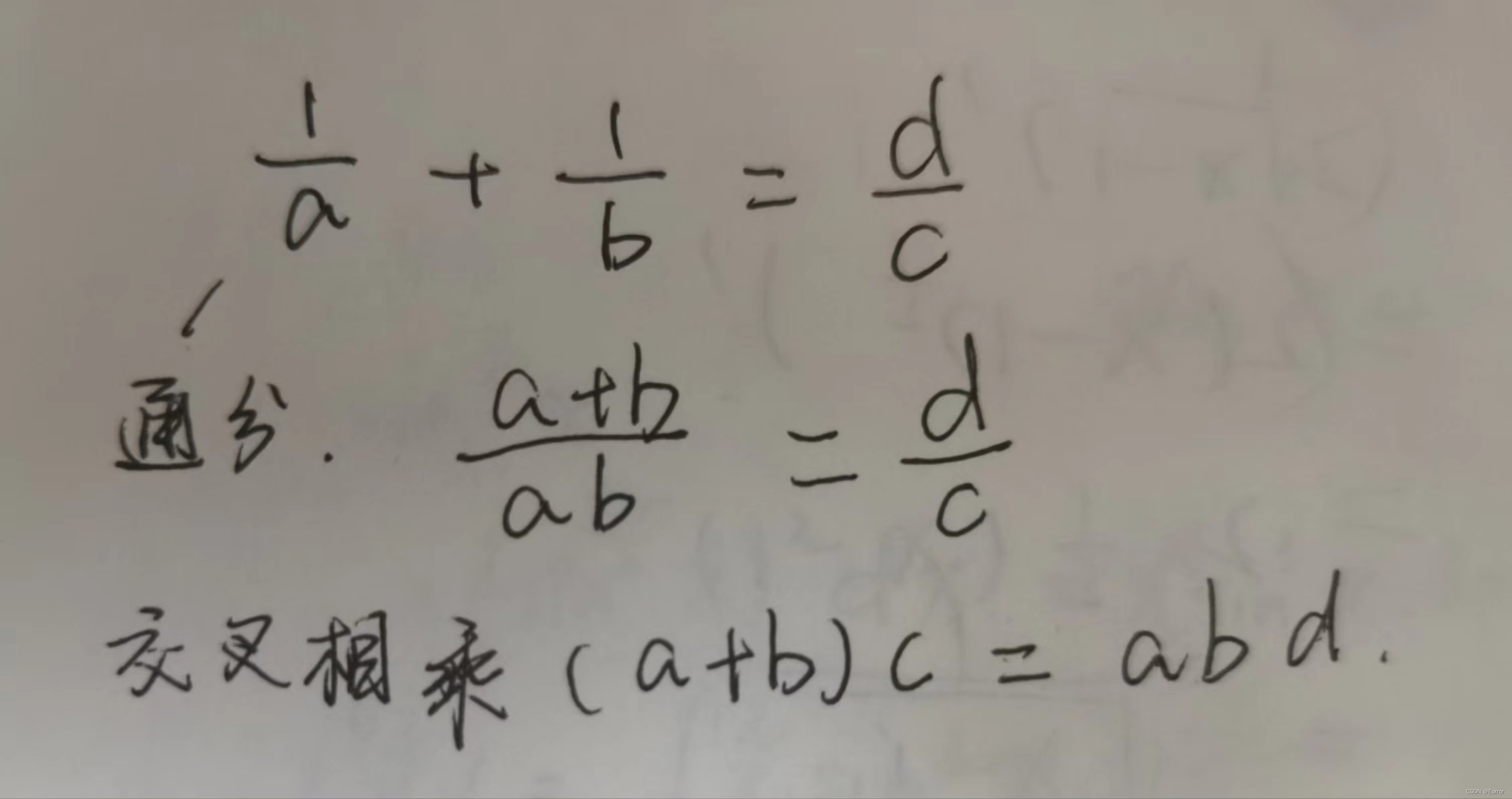
思路有了，代码如下：

#include<stdio.h>
int main (){
	int c =2, d =45;
  	int p = d / c ;
 	int count =0;
 	for (int i = p+1; i<=p*2;i++){
/**为了节约循环次数，直接从分母的一半开始循环，p+1是为了防止出现1/a本身大于1/45，
1/b出现负数的情况。
1/2p*2就等于c/d,所以不会有再超过它的了**/
	  	int a = i ;
 		int b = a * d /( a*n- d );
 		if (( a + b )* d == a * b * c){
 			count++;
 		}
	}
 
 	printf ("%d\n", count);
 	return 0;
}

 plus版（随便输啥都行）

#include<stdio.h>
int main (){
	int n,d;
 	scanf ("%d/%d",&n,&d);
 	int p = d / n;
 	int count =0;
 	for (int i = p+1; i<=p*2;i++){
	  	int a = i ;
 		int b = a * d /( a*n- d );
 		if (( a + b )* d == a * b * n ){
 			count++;
 			 printf ("%d:1/%d +1/%d =2/45\n", count , a , b );
		 }
	}
 

 	printf (" total answers :%d\n ", count );
 	return 0;
}