激活函数(Activation Function)
什么是激活函数?
人工神经网络的激活函数就是模仿生物神经网络。在生物神经网络中,信息的传递是通过神经元的树突和轴突的结合,(在前膜的内侧有致密突起和网格形成的囊泡栏栅,其空隙处正好容纳一个突触小泡,它可能有引导突触小泡与前膜接触的作用,促进突触小泡内递质的释放。当突触前神经元传来的冲动到达突触小体时,小泡内的递质即从前膜释放出来,进入突触间隙,并作用于突触后膜;如果这种作用足够大时,即可引起突触后神经元发生兴奋或抑制反应),黄字部分是来自某百科的解释,高中也学过,读不懂也没有关系,下面来点大白话的。如下图红色的圈圈,树突会产生一些物质,不断断积累,当到达一定程度的时候,信息就会传递给轴突,差不多就是这个过程,当然严谨的来说,信息传递的过程十分的复杂,就如黄字部分说的那样。

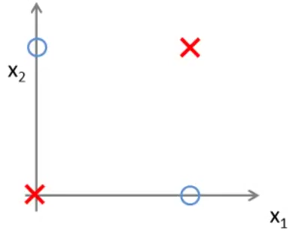
对于人工神经网络而言,是想用机器来尽可能的模仿生物神经元信息传递的过程。人工神经网络的定义通常是 y = w x + b y=wx+b y=wx+b的形式,通过多层神经元的叠加,来拟合复杂的函数。考虑一个问题,如果只是简单的通过累加的形式进行处理的话,那么神经网络能实现的功能是十分有限的。简单的例子,如下图所示,下面的数据是线性不可分的,是一个异或问题,只是通过 w x + b wx+b wx+b 是无法实现的。这时就需要加入非线性元素来改变,可以使得神经网络输出非线性决策边界。特别是多层神经网络,加入非线性元素,可以使得神经网络任意逼近任何非线性函数。
另一方面,激活函数还可以起到将数据特征映射到新的特征空间的作用,这样可以更加有利于数据的训练,加速模型的收敛。
激活函数
常用的激活函数Sigmoid、Tanh、ReLU、Leaky ReLU、PReLU,还有一些他们的变体以及其他的函数。这篇文章列举了26种激活函数,这里是原文,可能需要翻墙,小伙伴可以点击去看一下。
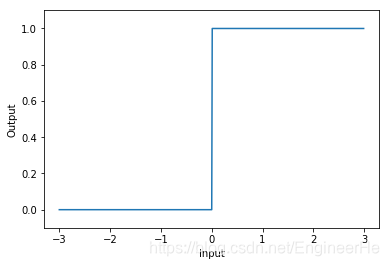
step function
f ( x ) = { 1 x > 0 0 x ≤ 0 f\left( x \right) = \left\{ {\begin{array}{c} {\begin{array}{c} 1&{x > 0} \end{array}}\\ {\begin{array}{c} 0&{x \le 0} \end{array}} \end{array}} \right. f(x)={1x>00x≤0
import numpy as np
import matplotlib.pyplot as plt
def step_func(x):
# if x > 0:
# return 1
# else:
# return 0
return np.array(x > 0, dtype=np.int)
x = np.arange(-3,3,0.01)
y = step_func(x)
plt.xlabel("Input")
plt.ylabel("Output")
plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show()
Sigmoid
Sigmoid函数是传统神经网络中最常用的激活函数,虽然现在已经不常用,但当年还是十分受欢迎的。Sigmoid函数也叫Logistic 函数,值域在0到1之间。
Sigmoid函数的表达式及其求导:
σ
(
x
)
=
1
1
+
e
−
x
∂
σ
(
x
)
∂
x
=
e
−
x
1
+
e
−
x
=
σ
(
x
)
(
1
−
σ
(
x
)
)
\begin{array}{l} \sigma \left( x \right) = \frac{1}{{1 + {e^{ - x}}}}\\ \frac{{\partial \sigma \left( x \right)}}{{\partial x}} = \frac{{{e^{ - x}}}}{{1 + {e^{ - x}}}} = \sigma \left( x \right)\left( {1 - \sigma \left( x \right)} \right) \end{array}
σ(x)=1+e−x1∂x∂σ(x)=1+e−xe−x=σ(x)(1−σ(x))
import numpy as np
# sigmoid函数
def sigmoid(x):
y = 1/(1+np.exp(-x))
return y
# sigmoid函数求导
def d_sigmoid(x):
dx = sigmoid(x)*(1-sigmoid(x))
return dx
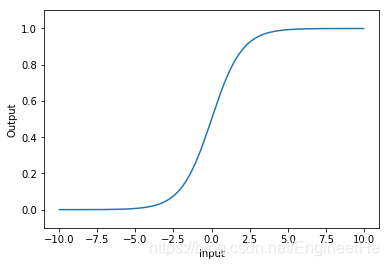
sigmoid激活函数
sigmoid函数导数
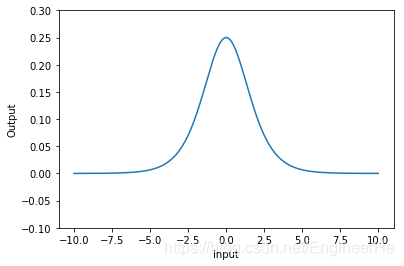
当x的值趋近负无穷的时候,y趋近于0;x趋近于正无穷的时候,y趋近于1;在 [ − 2 , 2 ] [-2, 2] [−2,2] 区间内,梯度变化比较明显,即x发生很小的变化,y变化的也比较明显。
sigmoid的优缺点:
优点:
- Sigmoid函数的输出映射在(0,1)之间,单调连续,输出范围有限,优化稳定
- 求导容易
缺点:
- 幂运算,计算成本高
- 容易出现梯度弥散(反向传播时,很容易就会出现梯度消失的情况,从而无法完成深层网络的训练)
- 不是以0为中心,为导致收敛速度下降(具体解释可以参考这里)
tanh
双曲正切函数,tanh函数输出以0为中心,区间为
[
−
1
,
1
]
[-1, 1]
[−1,1],tanh可以想象成两个sigmoid函数放在一起,性能要高于sigmoid函数
σ
(
x
)
=
e
x
−
e
−
x
e
x
+
e
−
x
\sigma \left( x \right) = \frac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^{ - x}}}}
σ(x)=ex+e−xex−e−x
tanh函数的变形:
σ
(
x
)
=
1
−
e
−
2
x
1
+
e
−
2
x
=
2
s
i
g
m
o
i
d
(
2
x
)
−
1
\sigma \left( x \right) = \frac{{1 - {e^{ - 2x}}}}{{1 + {e^{ - 2x}}}} = 2sigmoid\left( {2x} \right) - 1
σ(x)=1+e−2x1−e−2x=2sigmoid(2x)−1
求导:
∂
σ
(
x
)
∂
x
=
(
e
x
+
e
−
x
)
2
−
(
e
x
−
e
−
x
)
2
(
e
x
+
e
−
x
)
2
=
1
−
σ
2
(
x
)
\frac{{\partial \sigma \left( x \right)}}{{\partial x}} = \frac{{{{\left( {{e^x} + {e^{ - x}}} \right)}^2} - {{\left( {{e^x} - {e^{ - x}}} \right)}^2}}}{{{{\left( {{e^x} + {e^{ - x}}} \right)}^2}}} = 1 - {\sigma ^2}\left( x \right)
∂x∂σ(x)=(ex+e−x)2(ex+e−x)2−(ex−e−x)2=1−σ2(x)
def tanh(x):
# y = np.tanh(x)
y = 2*sigmoid(2*x)-1
return y
def d_tanh(x):
dx = 1- tanh(x)*tanh(x)
return dx
tanh激活函数
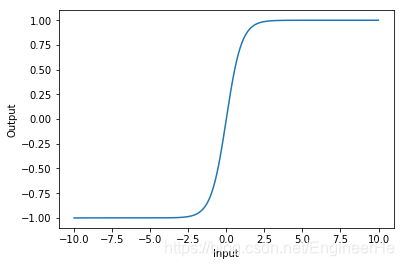
tanh激活函数求导
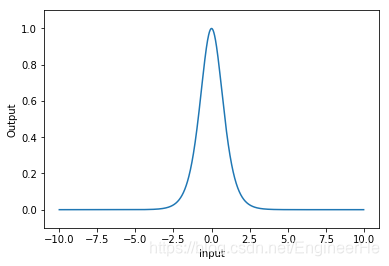
tanh函数的优缺点:
优点:只要是解决了sigmoid关于zero-centered的输出问题。导数范围变大,在 ( 0 , 1 ) (0,1) (0,1)之间,而sigmoid在 ( 0 , 0.25 ) (0, 0.25) (0,0.25) 之间,梯度消失问题有所缓解。
缺点:
- 幂运算,计算成本高
- 梯度消失问题
ReLU
Relu(Rectified Linear Unit)-修正线性单元函数,函数的表达式:
σ
(
x
)
=
{
x
x
>
0
0
x
≤
0
\sigma \left( x \right) = \left\{ {\begin{array}{ccc} {\begin{array}{ccc} x&{x > 0} \end{array}}\\ {\begin{array}{ccc} 0&{x \le 0} \end{array}} \end{array}} \right.
σ(x)={xx>00x≤0
即 ReLU=max(0, x)
def relu(x):
# 1
# y = np.maximum(0, x)
# 2
# y = np.where(x>0, x, 0)
# 3
y = (x + np.abs(x))/2
return y
ReLU激活函数
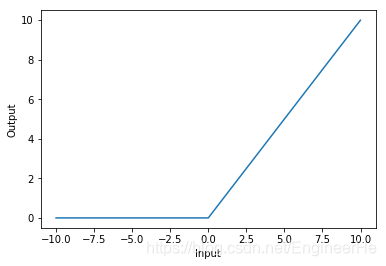
从图上可以看出,当 x ≤ 0 x \le 0 x≤0 的时候,ReLu有饱和问题,当 x > 0 x>0 x>0 的时候,则存在硬饱和(当x<0时,导数恒等于0;软饱和,导数趋近于0)。所以当 x > 0 x>0 x>0 的时候不会存在梯度消失的问题。为了解决左硬饱和问题,提出了Leaky ReLU**、**PReLU解决方法。Leaky ReLU的函数公式为: σ ( x ) = max ( α x , x ) \sigma \left( x \right) = \max (\alpha x,x) σ(x)=max(αx,x),其中 α \alpha α 是一个很小的值,这样做可以使得负轴的信息不会全部丢失,解决ReLU神经元死亡问题
def leaky_relu(x, leak):
y = np.maximum(leak*x, x)
return y
Leaky ReLU:
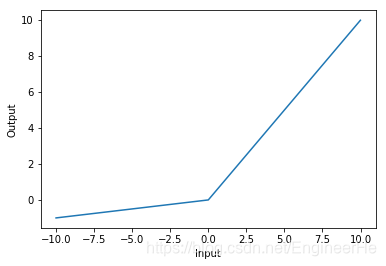
PReLU和Leaky ReLU的表达式相同,
σ
(
x
)
=
max
(
α
x
,
x
)
\sigma \left( x \right) = \max (\alpha x,x)
σ(x)=max(αx,x),区别在于这里的
α
\alpha
α 不是固定的,而是一个可以学习的参数。
ReLU激活函数的优缺点
优点:
- 梯度不饱和,收敛速度快;
- 相对于sigmoid/tanh激活函数,极大的改善了梯度消失的问题;
- 不需要进行指数运算,因此运算速度快、复杂度低
缺点:
- 对参数初始化和学习率非常敏感,存在神经元死亡;
- ReLU的输出均值也大于0,偏移现象和 神经元死亡会共同影响网络的收敛性;
ReLU激活函数为什么比sigmoid和tanh好?
- 相比Sigmoid和tanh,ReLU摒弃了复杂的计算(这里指的是幂运算),提高了运算速度;
- 对于深层的网络而言,Sigmoid和tanh函数反向传播的过程中,和容易出现梯度消失的问题;
- ReLU会使一部分神经元的输出为0,这样就造成了网络的稀疏性,并且减少了参数的相互依存关系,缓解了过拟合问题的发生。
ReLU激活函数为什么能解决梯度消失问题?

∂
C
∂
b
1
=
σ
′
(
z
1
)
w
2
σ
′
(
z
2
)
w
3
σ
′
(
z
3
)
w
4
σ
′
(
z
4
)
∂
C
∂
a
4
\frac{{\partial C}}{{\partial b1}} = \sigma '\left( {{z_1}} \right){w_2}\sigma '\left( {{z_2}} \right){w_3}\sigma '\left( {{z_3}} \right){w_4}\sigma '\left( {{z_4}} \right)\frac{{\partial C}}{{\partial {a_4}}}
∂b1∂C=σ′(z1)w2σ′(z2)w3σ′(z3)w4σ′(z4)∂a4∂C
上面的内容图片公式点 这里。假如对 b1进行反向传播,求梯度,公式如上,
σ
(
.
)
\sigma(.)
σ(.)表示激活函数,假如我们选择的是sigmoid函数,可以从上文中得知,sigmoid最大的梯度是0.25,所以在反向传播的过程中,梯度的下降呈指数下降,所以很容易造成梯度消失,使得前层网络的权值无法更新或者更新的很慢。选用ReLu函数,当
x
>
0
x>0
x>0 时,激活函数的梯度恒等于1,所以就可以大大解决了梯度消失的问题。
ReLU激活函数导致神经元“死亡”问题
设 y = w x + b y=wx+b y=wx+b 经过 σ ( x ) \sigma(x) σ(x)激活以后为a(其中的 σ \sigma σ 表示ReLU),定义损失函数为 L L L
一个简单的前馈网络传递的过程可以见到的表示如下:
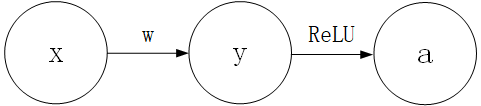
即 y = w x + b , a = σ ( y ) y=wx+b, a=\sigma(y) y=wx+b,a=σ(y)
反向传播的话就是根据链式求导法则,要更新
w
w
w ,所以对
w
w
w 进行求导:
∂
L
∂
w
=
∂
L
∂
a
⋅
∂
a
∂
y
⋅
∂
y
∂
w
=
∂
L
∂
a
⋅
∂
a
∂
y
⋅
x
T
=
∂
L
∂
y
⋅
x
T
\begin{array}{l} \frac{{\partial L}}{{\partial w}} &= \frac{{\partial L}}{{\partial a}} \cdot \frac{{\partial a}}{{\partial y}} \cdot \frac{{\partial y}}{{\partial w}}\\ &= \frac{{\partial L}}{{\partial a}} \cdot \frac{{\partial a}}{{\partial y}} \cdot {x^T}\\ &= \frac{{\partial L}}{{\partial y}} \cdot {x^T} \end{array}
∂w∂L=∂a∂L⋅∂y∂a⋅∂w∂y=∂a∂L⋅∂y∂a⋅xT=∂y∂L⋅xT
设学习率
l
r
lr
lr (learning rate)为定值,权重
w
w
w 的更新取决于
∂
L
∂
w
\frac{{\partial L}}{{\partial w}}
∂w∂L,
∂
L
∂
w
\frac{{\partial L}}{{\partial w}}
∂w∂L越大,则更新的越多, 即:
w
=
w
+
l
r
⋅
∂
L
∂
w
w = w + lr \cdot \frac{{\partial L}}{{\partial w}}
w=w+lr⋅∂w∂L
就上式而言,如果
l
r
lr
lr 的值设置的太大,权重就会更新的很多,这么一种情况,由于权重更新的太多,可能对于任意训练数据
x
x
x ,输出结果
y
y
y 都小于零,此时经过 ReLU 后,
a
=
m
a
x
(
0
,
x
)
=
0
a = max(0, x) = 0
a=max(0,x)=0 。这样的话会出现什么情况,根据上文我们说的ReLU函数求导,当
≤
0
\le 0
≤0 的时候,梯度为0;当
>
0
>0
>0 的时候梯度为1, 所以
∂
a
∂
y
=
0
\frac{{\partial a}}{{\partial y}} = 0
∂y∂a=0,即
∂
L
∂
w
=
∂
L
∂
a
⋅
0
⋅
∂
y
∂
w
=
0
\frac{{\partial L}}{{\partial w}} = \frac{{\partial L}}{{\partial a}} \cdot 0 \cdot \frac{{\partial y}}{{\partial w}} = 0
∂w∂L=∂a∂L⋅0⋅∂w∂y=0, 可以看出此后
w
w
w 就会停止更新,所以就会好造成该部分的神经元 “死亡”。
欢迎大家关注我的个人公众号,同样的也是和该博客账号一样,专注分享技术问题,我们一起学习进步






 本文深入探讨了激活函数在人工神经网络中的关键作用,包括Sigmoid、Tanh、ReLU及其变体等,分析了它们的数学特性、优缺点及应用场景。
本文深入探讨了激活函数在人工神经网络中的关键作用,包括Sigmoid、Tanh、ReLU及其变体等,分析了它们的数学特性、优缺点及应用场景。
















 3182
3182

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








