Fourier 变换的四种形式

• 首更 Date: 2016-08-26 15:37:45
• 二更 Date: 2018-12-30

关于傅里叶分析的背景和研究意义，相关博文已经介绍很清楚，无需赘述。本文直接从函数分解角度对傅里叶变换四种不同定义和相互之间关系进行总结。

傅里叶变换是信号的一种描述方式，主要通过增加频域视角，将时域复杂波形表示为简单的频率函数，获取时域不易发现的与信号有关的其他特性，例如频率或者随频率变化的振幅、相位等信息。当然，关于信号的描述方式可以有很多种，如时频分析，以及分数域信号分析等，并不仅仅局限于时域分析或者频域分析。概括来讲，

信号的描述就是基函数表征方法，即：如何找到合适的基函数空间，将要研究的对象分解成该基函数的线性组合形式（累加或者积分）。#线性分解

一、数学基础—内积空间正交分解

这部分主要简单回顾了与傅里叶分析相关的数学知识，主要参考文献是《高等代数》[王萼芳，石生明 修订]。

1.1 向量空间

线性空间

非空集合$V$中元素+某个数域$P$定义的加法、数乘运算（满足一定性质）=数域$P$上的线性空间$V$。

• 通常线性空间中的元素也被称为是向量，这里向量的意义要比几何中向量的意义宽泛许多，所以线性空间也被称为是向量空间；
• 这里的加法和数乘仅抽象意义，不同线性空间具有不同的具体表现。

显然线性空间$V$中含有的元素可以很多，那么定义了运算后，元素之间是否有关系？

基

基的概念是通过向量的线性无关引入的，所以先介绍一下线性无关：

线性空间$V$中，在数域$P$仅在$k_i=0,i=1,2,...,r$时下列等式成立
$$k_1{\alpha }_1+k_2{\alpha }_2....+k_r{\alpha }_r=0$$
则称向量${\alpha }_1,{\alpha }_2,...,{\alpha }_r$是线性无关的。

线性无关的向量个数会引出线性空间维度的概念，而维度是线性空间一个非常重要的属性。

如果在线性空间$V$中有$n$个线性无关的向量，但是没有更多数目的线性无关向量，那么$V$是$n$维的，这$n$个线性无关的向量称为$n$维线性空间的基；
如果在在线性空间$V$中可以找到任意多个线性无关的向量，则称$V$是无穷维的，任意多个线性无关的向量称为线性空间的基。

针对$n$维空间，其实就是$n$个线性无关向量张成的空间，该空间中任意一个向量都可以用这组基函数线性表出，即

V=Span{α1,α2,...,αr}V=Span\{\alpha_1,\alpha_2,...,\alpha_r\}V=Span{α1​,α2​,...,αr​}
或者说，$\alpha \in V$,则
$$\alpha =k_1{\alpha }_1+k_2{\alpha }_2....+k_r{\alpha }_r，k_i\in P,i=1,2,...r$$
且系数$k_i$唯一。

1.2 内积空间

上小节主要介绍了线性空间中一些相关概念，仅在集合上定义了加法和数乘运算，缺乏度量的概念，也就是线性空间中的概念还不足以对向量长度、夹角进行描述，为此引入内积空间概念。

数域P上线性空间+满足一定条件的映射$<\cdot ,\cdot >:V^2\to P$=内积空间

当然，根据数域的不同，内积也有不同的表现形式。

有了内积就能定义

• 向量的长度：$|\alpha |=\sqrt{<\alpha ,\alpha >}$；
• 向量之间夹角=$\arccos \frac{<\alpha ,\beta >}{|\alpha |\cdot |\beta |}$；
• 正交：$<\alpha ,\beta >=0$

而正交是一个非常好的性质，因为若基向量相互正交，针对$n$维空间中元素通过基向量表出的系数就能确定了，计算方法如下：
$$\beta =k_1{\alpha }_1+k_2{\alpha }_2....+k_r{\alpha }_r$$
通过内积运算：
$$<\beta ,{\alpha }_i>=<k_1{\alpha }_1+k_2{\alpha }_2....+k_r{\alpha }_r,{\alpha }_i>$$
可得
$$k_i=\frac{<\beta ,{\alpha }_i>}{<{\alpha }_i,{\alpha }_i>}$$

二、 傅里叶变换四种定义

本节开始，我们讨论一下傅里叶变换为什么会有四种不同形式的定义以及他们之间的联系。

2.1 总述

产生四种不同形式的傅里叶变换，关键在于线性空间中元素性质的不同，这里主要针对连续不连续，周期不周期对空间中元素分为了4类。具体如下：

信号类型

	连续	离散
周期	第1类	第3类
非周期	第2类	第4类
根据时间域信号$x$自变量的不同，可将信号分为连续信号$x(t)$和离散序列$x[n]$；根据信号周期性的不同，又可将两种不同类型信号分为周期性或非周期的，故待分析的信号类型有四种形式，导致傅里叶变换分成四类。

变换类型

周期性连续信号    <------> 傅立叶级数(Fourier Series,FS) 
非周期性连续信号  <------> 傅里叶变换（Fourier Transform,FT）
周期性离散信号    <------> 离散傅立叶变换(Discrete Fourier Transform,DFT)
非周期性离散信号  <------> 离散时域傅立叶变换（Discrete Time Fourier Transform,DTFT）

2.2 四种傅里叶变换

2.2.1 连续信号的傅里叶分析

方法： 从一定条件下，周期性连续信号$x(t)$能分解成一组谐波函数的线性组合；通过取极限逼近非周期连续信号，可定义傅里叶变换。

定义 周期性

信号$x(t)$是周期的，如果存在一个正数$T$使得$$x(t+T)=x(t),t\in R$$ 其中，正数$T$称为信号$x(t)$的周期。满足上式最小的$T_0$称为信号$x(t)$的基波周期，$w_0=\frac{2\pi }{T_0}$称为信号$x(t)$的基波频率。

以下介绍一组特殊的周期信号：

谐波分量

假设周期性连续信号$x(t)$的基波周期为$T_0$，根据周期性的定义，可知任意$k{T}_0，k\in Z$也是信号$x(t)$的周期，则可得一组复指数信号$${\varphi }_k(t)=e^{jk{w}_{0}t},k为整数$$
该组信号称为谐波信号，是因为该组信号都以$T_0$为周期。

根据$k$的取值不同，谐波函数就不同，可知，该函数空间有无穷多元素。
令V={...,e−2jw0t,e−jw0t,1,ejw0t,ej2w0t,...，ejkw0t，...}V=\{...,e^{-2jw_0 t},e^{-jw_0 t},1,e^{jw_0 t},e^{j2w_0 t},...，e^{jkw_0 t}，...\}V={...,e−2jw0​t,e−jw0​t,1,ejw0​t,ej2w0​t,...，ejkw0​t，...}是谐波信号构成的线性空间.

其中需要明确谐波函数之间的正交性，
$$<e^{jk{w}_{0}t},e^{jl{w}_{0}t}>={\int }_{T_0}{e}^{jk{w}_{0}t}{e}^{-jl{w}_{0}t}dt=\{\begin{array}{clc}{T}_0,& & k=l\\ 0,& & k\ne l\end{array}$$

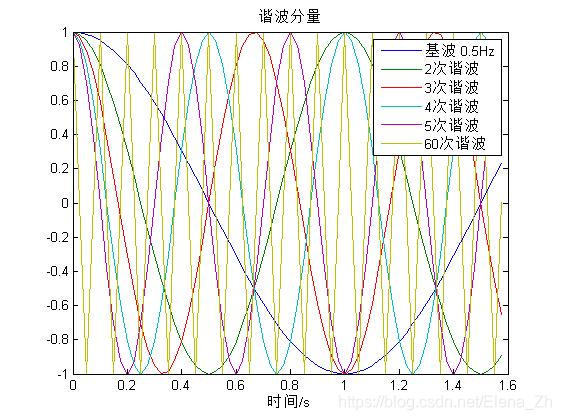
到此，我们只是说谐波分量之间是相互正交的，那么在它们张成的线性空间中，
V=Span{...,e−2jw0t,e−jw0t,1,ejw0t,ej2w0t,...，ejkw0t，...}V=Span\{...,e^{-2jw_0 t},e^{-jw_0 t},1,e^{jw_0 t},e^{j2w_0 t},...，e^{jkw_0 t}，...\}V=Span{...,e−2jw0​t,e−jw0​t,1,ejw0​t,ej2w0​t,...，ejkw0​t，...}
元素的系数就非常容易求解。

傅里叶级数（FS）

数学上对应于如下问题：

$$x(t)=\sum _{k=-\infty }^{+\infty }{c}_k{\varphi }_k(t)=\sum _{k=-\infty }^{+\infty }{c}_k{e}^{jk{w}_{0}t}$$

如何将上述式子中的系数$c_k$解出来。基于上述数学基础，我们很容易求出：

$$c_k=\frac{<x(t),e^{jk{w}_{0}t}>}{<e^{jk{w}_{0}t},e^{jk{w}_{0}t}>}=\frac{1}{T_0}{\int }_{T_0}x(t)e^{-jk{w}_{0}t}dt,k为整数$$
其中$a_k$称为为傅里叶系数，通常是复数，代表某一谐波分量所占的权重。

傅里叶级数主要是将周期连续信号用一组谐波函数表示出来，可见周期性导致了另外一个域的离散性。

傅里叶变换（FT）

如果信号$x(t)$不再是周期性连续信号，而是一般的非周期信号，如何用上述函数空间将其表征出来？

主要的思路是，将信号$x(t)$以周期$T_0$延拓为$\tilde{x}(t)$, 通过$\tilde{x}(t)$的傅里叶级数，将周期$T_0$取无穷大，得到最终结果。

1. 首先，周期延拓后的信号$\tilde{x}(t)$可表征为，
   $$\tilde{x}(t)=\sum _{k=-\infty }^{+\infty }{c}_k{e}^{jk{w}_{0}t},$$$$c_k=\frac{1}{T_0}{\int }_{T_0}\tilde{x}(t)e^{-jk{w}_{0}t}dt=\frac{1}{T_0}{\int }_{-T_0/2}^{T_0/2}x(t)e^{-jk{w}_{0}t}dt$$此处利用了被积函数的周期性，将积分区间转化到一个确定的周期内，且该周期内$x(t)=\tilde{x}(t)$。
2. 接着，通过对$\tilde{x}(t)$频谱的分析，发现在周期$T_0$逐渐增大过程中，$c_k$逐渐变为无穷小，这对于我们研究信号的频域特性而言，已然没有什么意义了。庆幸的是，我们发现$T_0{c}_k$在极限过程中不是趋于无穷小的，令$$X(jk{w}_0)=T_0{c}_k={\int }_{-T_0/2}^{T_0/2}x(t)e^{-jk{w}_{0}t}dt$$则周期信号$\tilde{x}(t)$表征为
   $$\tilde{x}(t)=\frac{1}{2\pi }\sum _{k=-\infty }^{+\infty }X(jk{w}_0)e^{jk{w}_{0}t}{w}_0，$$这个式子其实就是微积分中的极限和，是定积分研究曲边梯形等意义时产生的和式。
3. 取极限, $T\to \infty ,w_0=\frac{2\pi }{T_0}\to dw$：

$$\begin{gathered} x(t)=\underset{T\to +\infty }{\lim }\tilde{x}(t)=\underset{T\to +\infty }{\lim }\frac{1}{2\pi }\sum _{k=-\infty }^{+\infty }X(jk{w}_0)e^{jk{w}_{0}t}{w}_0=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }X(jw)e^{jwt}dw, \\ X(jw)=\underset{T\to +\infty }{\lim }X(jk{w}_0)=\underset{T\to +\infty }{\lim }{T}_0{c}_k=\underset{T\to +\infty }{\lim }{\int }_{-T_0/2}^{T_0/2}x(t)e^{-jk{w}_{0}t}dt={\int }_{-\infty }^{+\infty }x(t)e^{-jwt}dt \end{gathered}$$

综合式$$x(t)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }X(jw)e^{jwt}dw$$傅里叶变换
$$X(jw)={\int }_{-\infty }^{+\infty }x(t)e^{-jwt}dt$$

在这个过程中也可以得到周期信号的傅里叶系数和傅里叶变换之间关系，即$$c_k=\frac{1}{T_0}X(jk{w}_0)=\frac{w_0}{2\pi }X(jk{w}_0)$$

周期信号$\tilde{x}(t)$的傅里叶级数正比于某一周期内信号傅里叶变换的样本值。

需要理解

$X(jw)=$的物理意义:频谱密度函数。

2.2.2 离散信号的傅里叶分析

这部分思路其实是平行于连续信号的分析，先从信号的周期性谈起

定义 周期性

信号$x[n]$是周期的，如果存在一个正整数$N$使得$$x[n+N]=x[n]$$对所有的$n$都成立。其中，正整数$N$为信号$x[n]$的周期。满足上式最小的$N$成为信号$x[n]$的基波周期，$w_0=2\pi /N$称为信号$x[n]$的基波频率。

离散谐波分量
$${\varphi }_k[n]=e^{jk\frac{2\pi }{N}n},k,n均为整数$$
此处，需要特别注意一下这组谐波函数的性质，
$${\varphi }_{k+N}[n]=e^{j(k+N)\frac{2\pi }{N}n}={\varphi }_k[n]$$更一般地，${\varphi }_{k+rN}[n]={\varphi }_k[n],r为整数$.

该性质说明什么问题？说明这组谐波信号以$N$为周期，有且仅有$N$个独立的谐波信号；或者可以理解为，此时张成函数空间为有限维数的。令
V=span{1,ej2πNn,ej22πNn,...,ej(N−1)2πNn} V=span\{1,e^{j\frac{2\pi}{N}n},e^{j2\frac{2\pi}{N}n},...,e^{j(N-1)\frac{2\pi}{N}n}\}V=span{1,ejN2π​n,ej2N2π​n,...,ej(N−1)N2π​n}

这点区别于连续情形下张成的空间由无穷多个线性无关的函数。

谐波信号是不是正交的？是的！

这点需要通过离散序列之间的内积定义，
$$<x,y>=x\cdot y=\sum _{n=0}^{N-1}x[n]y[n]$$
和
$$\sum _{n=(N)}{e}^{jk\frac{2\pi }{N}n}=\{\begin{array}{clc}N,& & k=lN,l\in Z\\ 0,& & k其他\end{array}$$
验证。

接下来，要考虑的问题是如何用这组谐波信号将周期离散信号表征出来？

离散傅里叶级数

已知周期为$N$的离散信号$x[n]$,考虑如何用$N$个不同的谐波分量将信号表征，其实是解决这样一个数学问题:

如何根据已知的序列$x[n]$算出系数$a_k$
$$x[n]=\sum _{k=<N>}{a}_k{\varphi }_k[n]=\sum _{k=<N>}{a}_k{e}^{j\frac{2\pi }{N}kn}$$

• 方法一：解$n$维线性方程组，有唯一解
• 方法二：闭式表达式$$a_k=\frac{<x,{\varphi }_k>}{<{\varphi }_k,{\varphi }_k>}=\frac{1}{N}\sum _{n=<N>}x[n]e^{-j\frac{2\pi }{N}kn}$$

分别取对应周期上结果可得，

综合式$$x[n]=\sum _{k=0}^{N-1}{a}_k{e}^{j\frac{2\pi }{N}kn},$$离散傅里叶变换$$X[k]=\frac{1}{N}\sum _{n=0}^{N-1}x[n]e^{-j\frac{2\pi }{N}kn}$$

非周期性离散信号的傅里叶表示

如果信号$x[n]$不再具有周期性，而是一个有限长度的序列，则如何用上述的函数空间表征？

解决思路平行于连续信号的情形，即周期延拓的方法。

假设，$\tilde{x}[n]$是信号$x[n]$经过周期$N$延拓后的信号，则根据上述离散傅里叶级数，可将延拓后的信号表示为
$$\tilde{x}[n]=\sum _{k=<N>}{a}_k{\varphi }_k[n]=\sum _{k=<N>}{a}_k{e}^{j\frac{2\pi }{N}kn}$$其中傅里叶系数为
$$a_k=\frac{1}{N}\sum _{n=<N>}\tilde{x}[n]e^{-j\frac{2\pi }{N}kn}$$令
$$X(e^{jk{w}_0})=N{a}_k=\sum _{n=<N>}\tilde{x}[n]e^{-j\frac{2\pi }{N}kn}$$
取周期$N\to +\infty$，可得到

综合式
$$x[n]=\frac{1}{2\pi }{\int }_{2\pi }X(e^{jw})e^{jwn}dw$$
离散时间傅里叶变换(DTFT)
$$X(e^{jw})=\sum _{n=-\infty }^{+\infty }x[n]e^{-jwn}$$

发生的逼近效果需要和连续时情形进行区分，这也是比较难以理解的部分.