
目录
RLC 电路全面整理与汇总
RLC 电路是由 电阻 ®、电感 (L)、电容 © 三种基本电子元件组成的电路,是电子工程中的核心研究对象。它属于 二阶电路,其行为由二阶微分方程描述,具有丰富的动态特性。RLC 电路根据元件的连接方式分为 串联 RLC 电路 和 并联 RLC 电路,在滤波器、振荡器、谐振电路等应用中发挥重要作用。以下将从符号定义、基本概念、电路特性、响应分析、基尔霍夫定律、复频域分析、电路图绘制到应用领域进行全面讲解。
1. 符号与术语
以下是 RLC 电路分析中常用的符号及其含义:
| 符号 | 含义 | 单位 |
|---|---|---|
| R R R | 电阻 (Resistance) | 欧姆 ( Ω Ω Ω) |
| L L L | 电感 (Inductance) | 亨利 ( H H H) |
| C C C | 电容 (Capacitance) | 法拉 ( F F F) |
| V V V 或 v ( t ) v(t) v(t) | 电压 (Voltage) | 伏特 ( V V V) |
| I I I 或 i ( t ) i(t) i(t) | 电流 (Current) | 安培 ( A A A) |
| s s s | 复频率 (Complex Frequency) | 秒 − 1 ^{-1} −1 ( s − 1 s^{-1} s−1) |
| f f f | 频率 (Frequency) | 赫兹 ( H z Hz Hz) |
| f 0 f_0 f0 | 谐振频率 (Resonant Frequency) | 赫兹 ( H z Hz Hz) |
| Z Z Z | 阻抗 (Impedance) | 欧姆 ( Ω Ω Ω) |
| Y Y Y | 导纳 (Admittance) | 西门子 ( S S S) |
| ω \omega ω | 角频率 (Angular Frequency) | 弧度/秒 ( r a d / s rad/s rad/s) |
2. 基本概念
2.1 元件特性
-
电阻 ®
- 作用:阻碍电流流动,消耗能量并转化为热能。
- 阻抗:( Z R = R Z_R = R ZR=R )(纯实数,无频率依赖)。
-
电感 (L)
- 作用:阻碍电流变化,储存能量于磁场中,根据法拉第定律产生感应电动势 ( V L = L d i d t V_L = L \frac{di}{dt} VL=Ldtdi )。
- 感抗:( X L = ω L X_L = \omega L XL=ωL )(随频率增加而增大)。
-
电容 ©
- 作用:阻碍电压变化,储存能量于电场中,电流与电压关系为 ( I = C d v d t I = C \frac{dv}{dt} I=Cdtdv )。
- 容抗:( X C = 1 ω C X_C = \frac{1}{\omega C} XC=ωC1 )(随频率增加而减小)。
2.2 阻抗与导纳
-
阻抗 (Z)
- 定义:电路对交流电的阻碍能力,单位为欧姆 (Ω)。
- 复数形式:( Z = R + j X Z = R + jX Z=R+jX ),其中 ( X = X L − X C X = X_L - X_C X=XL−XC ) 是净电抗,( j j j ) 是虚数单位。
-
导纳 (Y)
- 定义:电路对交流电的导通能力,单位为西门子 (S),是阻抗的倒数 (( Y = 1 Z Y = \frac{1}{Z} Y=Z1 ))。
- 复数形式:( Y = G + j B Y = G + jB Y=G+jB ),其中 ( G = 1 R G = \frac{1}{R} G=R1 )(电导),( B = ω C − 1 ω L B = \omega C - \frac{1}{\omega L} B=ωC−ωL1 )(电纳)。
3. 串联 RLC 电路
3.1 电路特性
串联 RLC 电路中,电阻、电感、电容依次连接,电流通过每个元件相同,总电压为各元件电压之和。
-
电路图

-
总阻抗
Z = R + j ( ω L − 1 ω C ) Z = R + j\left( \omega L - \frac{1}{\omega C} \right) Z=R+j(ωL−ωC1) -
总导纳
Y = 1 Z = 1 R + j ( ω L − 1 ω C ) Y = \frac{1}{Z} = \frac{1}{R + j\left( \omega L - \frac{1}{\omega C} \right)} Y=Z1=R+j(ωL−ωC1)1
3.2 微分方程
瞬态分析中,串联 RLC 电路的电流 (
I
(
t
)
I(t)
I(t) ) 满足二阶微分方程:
L
d
2
I
(
t
)
d
t
2
+
R
d
I
(
t
)
d
t
+
1
C
I
(
t
)
=
d
V
s
(
t
)
d
t
L \frac{d^2 I(t)}{dt^2} + R \frac{d I(t)}{dt} + \frac{1}{C} I(t) = \frac{d V_s(t)}{dt}
Ldt2d2I(t)+RdtdI(t)+C1I(t)=dtdVs(t)
其中 (
V
s
(
t
)
V_s(t)
Vs(t) ) 是输入电压。
3.3 谐振频率
谐振发生在感抗等于容抗时 ((
ω
L
=
1
ω
C
\omega L = \frac{1}{\omega C}
ωL=ωC1 )):
f
0
=
1
2
π
L
C
f_0 = \frac{1}{2\pi \sqrt{LC}}
f0=2πLC1
- 在谐振时:总阻抗 ( Z = R Z = R Z=R )(最小值),电流达到最大。
4. 并联 RLC 电路
4.1 电路特性
并联 RLC 电路中,电阻、电感、电容并联连接,电压相同,各支路电流相加。
-
电路图
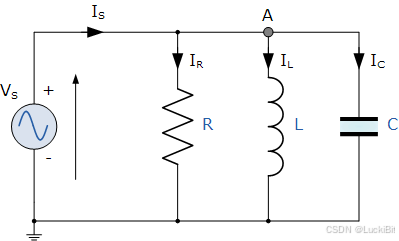
-
总导纳
Y = 1 R + j ( ω C − 1 ω L ) Y = \frac{1}{R} + j\left( \omega C - \frac{1}{\omega L} \right) Y=R1+j(ωC−ωL1) -
总阻抗
Z = 1 Y = 1 1 R + j ( ω C − 1 ω L ) Z = \frac{1}{Y} = \frac{1}{\frac{1}{R} + j\left( \omega C - \frac{1}{\omega L} \right)} Z=Y1=R1+j(ωC−ωL1)1
4.2 微分方程
瞬态分析中,并联 RLC 电路的电压 (
V
(
t
)
V(t)
V(t) ) 满足二阶微分方程:
C
d
2
V
(
t
)
d
t
2
+
1
R
d
V
(
t
)
d
t
+
1
L
V
(
t
)
=
d
I
s
(
t
)
d
t
C \frac{d^2 V(t)}{dt^2} + \frac{1}{R} \frac{d V(t)}{dt} + \frac{1}{L} V(t) = \frac{d I_s(t)}{dt}
Cdt2d2V(t)+R1dtdV(t)+L1V(t)=dtdIs(t)
其中 (
I
s
(
t
)
I_s(t)
Is(t) ) 是输入电流。
4.3 谐振频率
谐振发生在电纳为零时 ((
ω
C
=
1
ω
L
\omega C = \frac{1}{\omega L}
ωC=ωL1 )):
f
0
=
1
2
π
L
C
f_0 = \frac{1}{2\pi \sqrt{LC}}
f0=2πLC1
- 在谐振时:总阻抗 ( Z = R Z = R Z=R )(最大值),总电流最小。
5. 电路响应
RLC 电路的瞬态响应由特征方程的根决定,特征方程形式为:
s
2
+
R
L
s
+
1
L
C
=
0
(
串联
)
s^2 + \frac{R}{L} s + \frac{1}{LC} = 0 \quad (\text{串联})
s2+LRs+LC1=0(串联)
s
2
+
1
R
C
s
+
1
L
C
=
0
(
并联
)
s^2 + \frac{1}{RC} s + \frac{1}{LC} = 0 \quad (\text{并联})
s2+RC1s+LC1=0(并联)
根据根的性质,分为三种情况:
-
过阻尼
- 根为两个不相等的实数。
- 响应:无振荡,缓慢趋于稳定。
-
临界阻尼
- 根为两个相等的实数。
- 响应:无振荡,最快趋于稳定。
-
欠阻尼
- 根为一对共轭复数。
- 响应:振荡,振幅随时间衰减。
6. 基尔霍夫定律
6.1 基尔霍夫电流定律 (KCL)
- 定义:在任意节点,流入电流之和等于流出电流之和。
- 数学表达式:
∑ I 流入 = ∑ I 流出 \sum I_{\text{流入}} = \sum I_{\text{流出}} ∑I流入=∑I流出
6.2 基尔霍夫电压定律 (KVL)
- 定义:在任意闭合回路,电压升与电压降的代数和为零。
- 数学表达式:
∑ V 升 = ∑ V 降 \sum V_{\text{升}} = \sum V_{\text{降}} ∑V升=∑V降
7. 复频域分析
7.1 复频率 ( s )
复频率 ( s = σ + j ω s = \sigma + j\omega s=σ+jω ):
- ( σ \sigma σ ):衰减系数,决定信号衰减或增长。
- ( ω \omega ω ):角频率,决定振荡频率。
7.2 拉普拉斯变换
拉普拉斯变换将时域信号转换为复频域:
F
(
s
)
=
L
{
f
(
t
)
}
=
∫
0
∞
f
(
t
)
e
−
s
t
d
t
F(s) = \mathcal{L}\{f(t)\} = \int_{0}^{\infty} f(t) e^{-st} \, dt
F(s)=L{f(t)}=∫0∞f(t)e−stdt
7.3 元件复频域阻抗
- 电阻:( Z R = R Z_R = R ZR=R )
- 电感:( Z L = s L Z_L = sL ZL=sL )
- 电容:( Z C = 1 s C Z_C = \frac{1}{sC} ZC=sC1 )
7.4 串联 RLC 电路复频域阻抗
Z ( s ) = R + s L + 1 s C Z(s) = R + sL + \frac{1}{sC} Z(s)=R+sL+sC1
7.5 并联 RLC 电路复频域导纳
Y ( s ) = 1 R + s C + 1 s L Y(s) = \frac{1}{R} + sC + \frac{1}{sL} Y(s)=R1+sC+sL1
7.6 传递函数
传递函数 ( H ( s ) = V out ( s ) V in ( s ) H(s) = \frac{V_{\text{out}}(s)}{V_{\text{in}}(s)} H(s)=Vin(s)Vout(s) ) 用于分析频率响应和稳定性。
8. 使用 LaTeX 绘制 RLC 电路图
以下是使用 circuitikz 包绘制的串联和并联 RLC 电路图代码,可在 LaTeX 环境中编译。
8.1 串联 RLC 电路
\documentclass{standalone}
\usepackage{circuitikz}
\begin{document}
\begin{circuitikz}
\draw
(0,0) to[acsource, l=$V_{AC}$] (0,2) % 交流电源
(0,2) to[R, l=$R$] (2,2) % 电阻
(2,2) to[L, l=$L$] (4,2) % 电感
(4,2) to[C, l=$C$] (6,2) % 电容
(6,2) to[short] (6,0) % 连接到地
(6,0) node[ground]{} % 接地符号
(0,0) to[short] (6,0); % 闭合回路
\end{circuitikz}
\end{document}
8.2 并联 RLC 电路
\documentclass{standalone}
\usepackage{circuitikz}
\begin{document}
\begin{circuitikz}
\draw
(0,0) to[acsource, l=$V_{AC}$] (0,2) % 交流电源
(0,2) to[short] (2,2) % 上方节点
(2,2) to[R, l=$R$] (2,0) % 电阻支路
(2,2) to[L, l=$L$] (4,2) % 电感支路
(4,2) to[short] (4,0) % 电感接地
(2,2) to[C, l=$C$] (6,2) % 电容支路
(6,2) to[short] (6,0) % 电容接地
(0,0) to[short] (6,0) % 下方连接
(6,0) node[ground]{}; % 接地符号
\end{circuitikz}
\end{document}
9. 应用领域
RLC 电路在电子工程中有广泛应用:
| 应用领域 | 作用 |
|---|---|
| 谐振电路 | 选择特定频率信号(如收音机调谐) |
| 滤波器 | 低通、高通、带通、带阻滤波 |
| 振荡电路 | 产生稳定的交流信号(如振荡器) |
| 无线通信 | 调制与解调信号 |
| 电源电路 | 降噪、稳定电压 |
10. 总结
RLC 电路是电子工程的基础电路,其行为由 电阻、电感、电容 的特性决定。通过串联或并联连接,形成不同的电路特性:
- 串联 RLC:电流最大化,适用于信号放大和谐振电路。
- 并联 RLC:阻抗最大化,适用于滤波和稳压电路。
谐振频率 ( f 0 = 1 2 π L C f_0 = \frac{1}{2\pi \sqrt{LC}} f0=2πLC1 ) 是设计中的关键参数。通过 基尔霍夫定律 和 复频域分析(如拉普拉斯变换),可以深入研究电路的稳态和瞬态行为。
11. 结束语
- 本节内容已经全部介绍完毕,希望通过这篇文章,大家对
RLC电路有了更深入的理解和认识。- 感谢各位的阅读和支持,如果觉得这篇文章对你有帮助,请不要吝惜你的点赞和评论,这对我们非常重要。再次感谢大家的关注和支持!点我关注❤️


























 3401
3401

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










