【专题三】二分

本博客梳理二分算法

14. 在排序数组中查找元素的第一个和最后一个位置

二分核心原理与模板

14.1 解法一：暴力查找

从前往后遍历查找即可，慢就慢在：没有利用数组有序的特性，每次循环只能舍去一个点

14.2 解法二：二分

注意：并不是说数组有序才能用二分，而是找到问题中的二段性，就可以考虑二分

14.2.1 找左端点

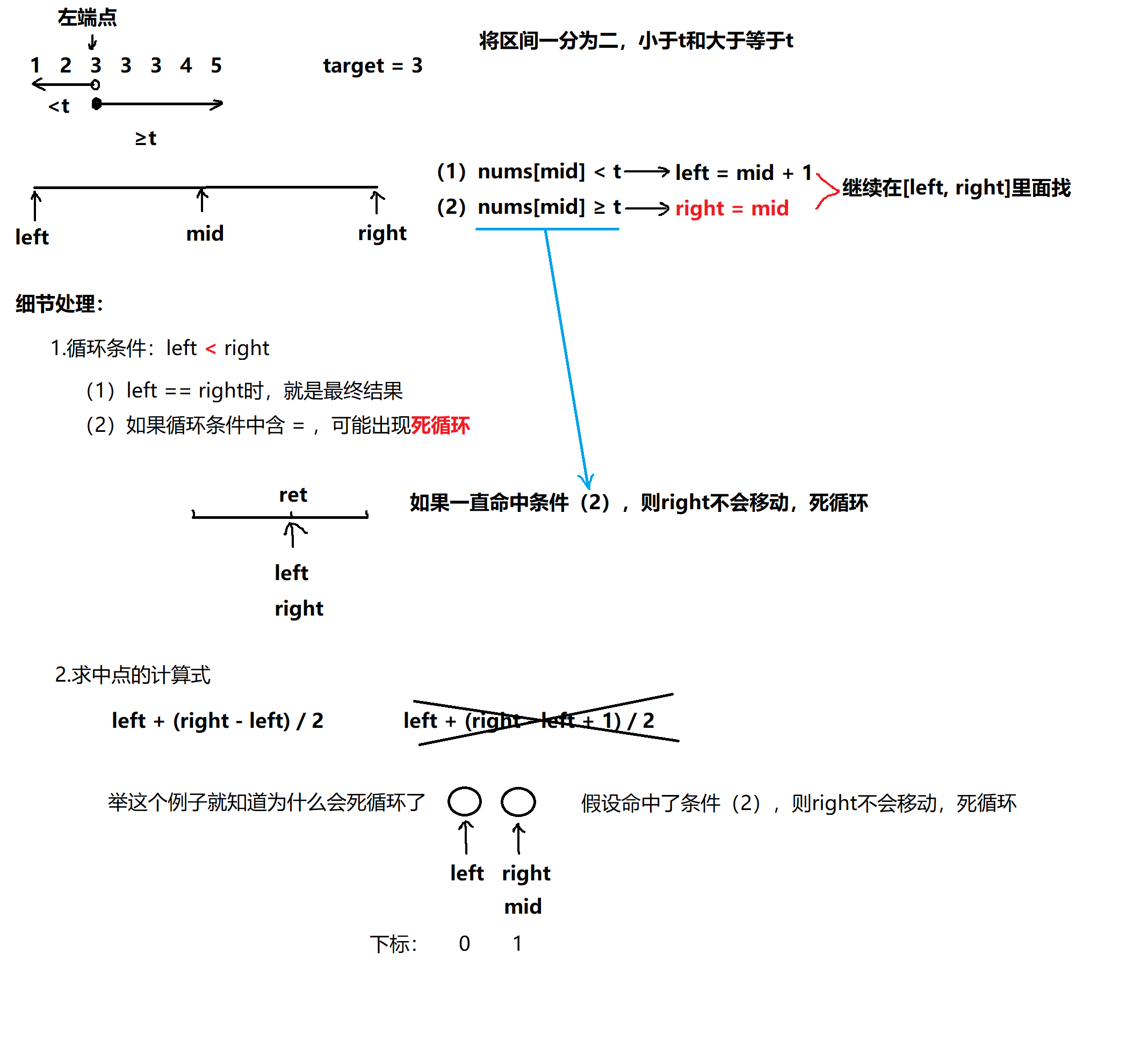
14.2.2 找右端点

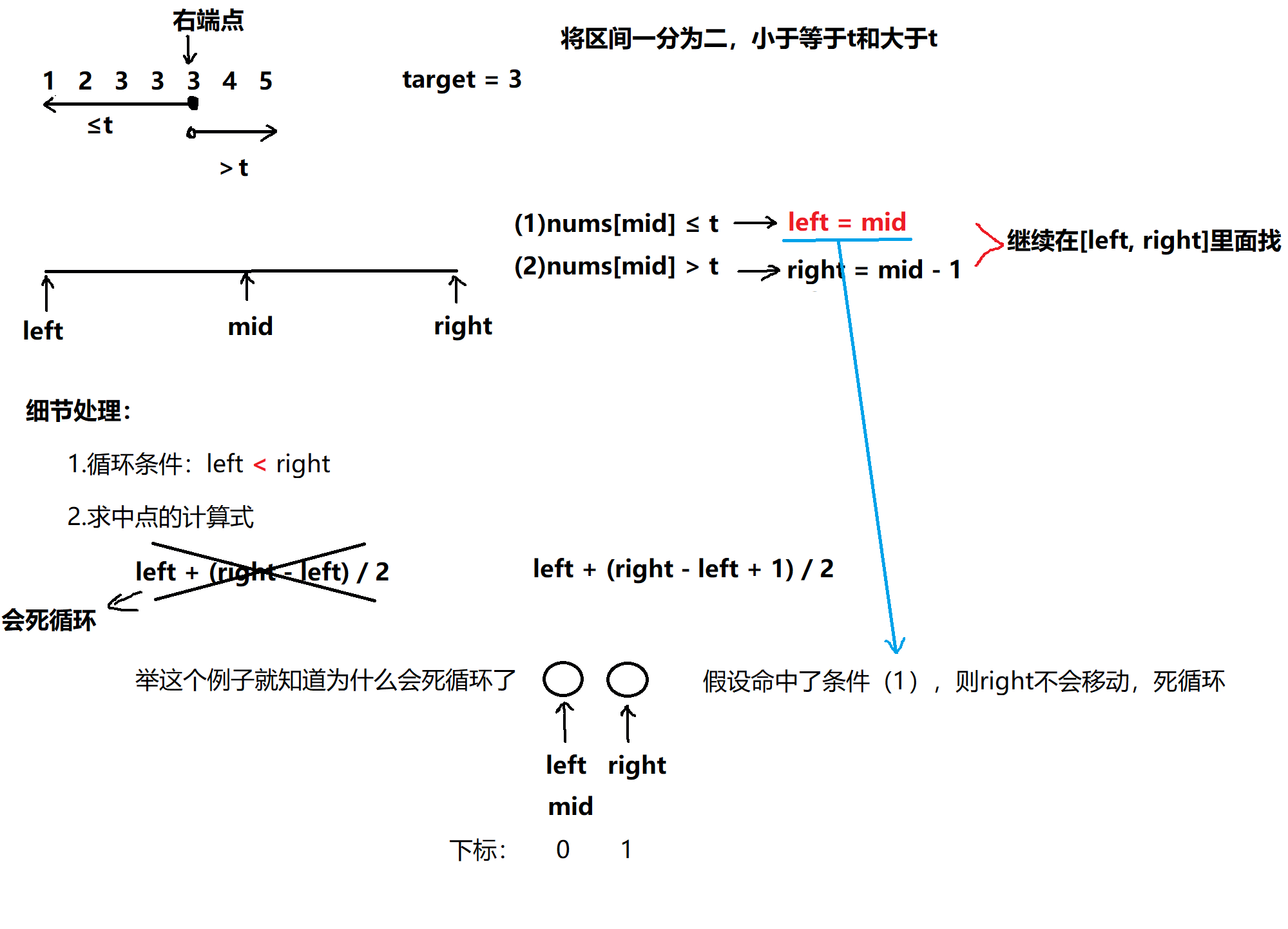
class Solution {
public:
    //二分模板题
    vector<int> searchRange(vector<int>& nums, int target) {
        if(nums.size() == 0)
            return {-1, -1};
        int left = 0, right = nums.size() - 1;
        vector<int> ret;

        //1.寻找区间左端点
        while(left < right)
        {
            int mid = left + (right - left) / 2;
            if(nums[mid] < target)
                left = mid + 1;
            else
                right = mid;
        }
        if(nums[left] == target)
            ret.push_back(left);
        else
            return {-1, -1};

        left = 0;
        right = nums.size() - 1;
        //2.寻找区间右端点（注：如果左端点找到了，那么右端点最极端就是和左端点重合，一定有）
        while(left < right)
        {
            int mid = left + (right - left + 1) / 2;
            if(nums[mid] <= target)
                left = mid;
            else
                right = mid - 1;
        }

        ret.push_back(left);
        return ret;
    }
};

从这个问题，我们可以提炼出一个二分查找的模板

 //1.寻找区间左端点
while(left < right)
{
    int mid = left + (right - left) / 2;
    if(nums[mid] < target)
        left = mid + 1;
    else
        right = mid;
}

 //2.寻找区间右端点
while(left < right)
{
    int mid = left + (right - left + 1) / 2;
    if(nums[mid] <= target)
        left = mid;
    else
        right = mid - 1;
}

记忆方法：如果算中点要“+1”，则下面right要 “-1”

下面两道题可以很好的体现：二分并不只适用于所谓数组有序的特点，问题中展现出二段性，就可以考虑采用二分查找

15. 寻找峰值

class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        //最左侧和最右侧都是负无穷
        //假设找到一个点，左边有单减趋势，则左边一定有山峰，右边同理
        int left = 0, right = nums.size() - 1;
        while(left < right)
        {
            int mid = left + (right - left) / 2;
            if(nums[mid] < nums[mid + 1])//找一个要更新left = mid + 1的情况，即山峰在右边，即mid右边有
            //山峰
                left = mid + 1;
            else
                right = mid;
        }
        return left;
    }
};

16. 寻找旋转排序数组中的最小值

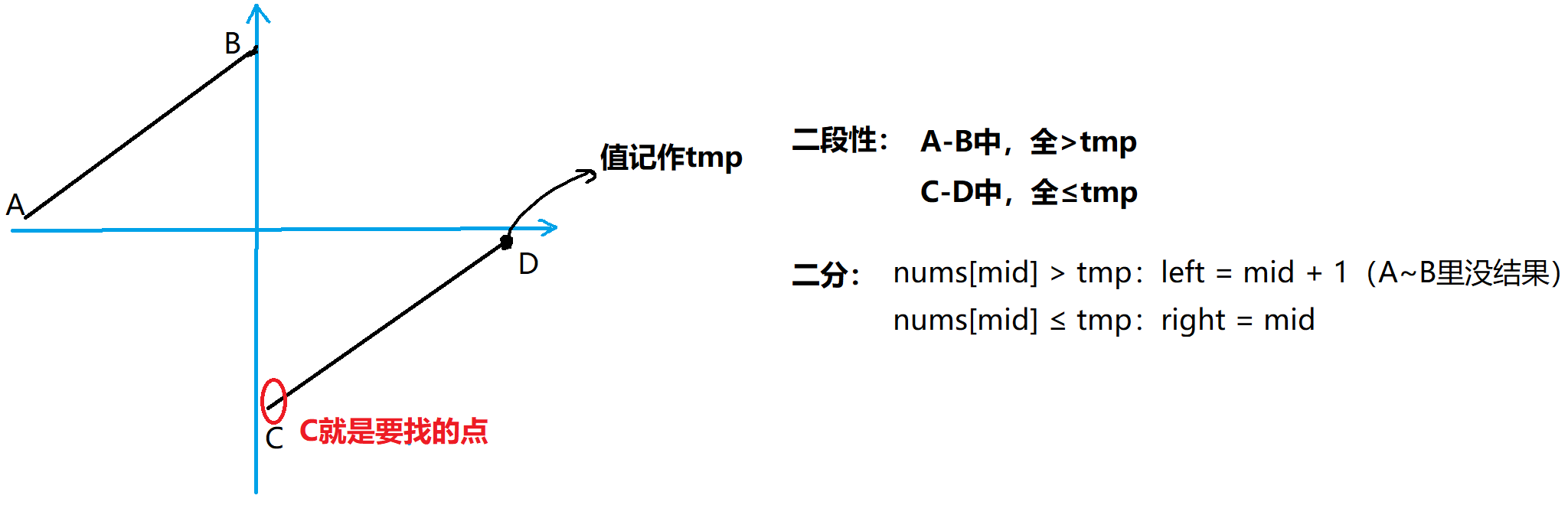
class Solution {
public:
    int findMin(vector<int>& nums) {
        int left = 0, right = nums.size() - 1;
        int tmp = nums[nums.size() - 1];

        while(left < right)
        {
            int mid = left + (right - left) / 2;
            if(nums[mid] > tmp)
                left = mid + 1;
            else
                right = mid;
        }
        return nums[left];
    }
};