合法矩阵的面积之和

最新推荐文章于 2025-07-27 15:31:34 发布

原创最新推荐文章于 2025-07-27 15:31:34 发布 · 324 阅读

0 ·

CC 4.0 BY-SA版权

单调栈专栏收录该内容

0 篇文章

订阅专栏

给出一张n*m（1<=n,m<=2000）的矩阵，’.’ 代表空地,’#’ 代表障碍物，合法矩阵为内部不含障碍物的矩阵。求出所有合法矩阵的面积之和。

input
2 3
.#.
…#
output
8

input
3 3
…
…
…
output
100

input
3 4
…#.
#…
…#
output
40
先预处理出一个数组dp，记录每个点向上最大的合法高度。对于每一行，维护底在这一行的矩阵的面积和。从左往右扫，利用单调栈维护高度。对于答案的更新只在pop的时候进行。如果当前列高大于栈顶，直接丢进去；如果相等
就跳过；如果当前列高小于栈顶，就把栈顶跳出并更新：
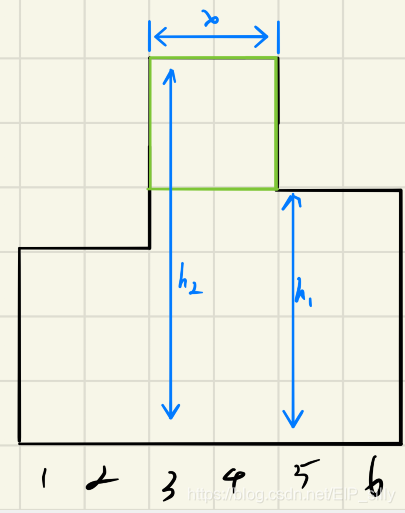
在这里插入图片描述
如图，计算绿色部分的贡献，即计算绿色部分能使底为3,4的矩阵增加多少合法矩阵的面积。或者说本来24的举证扩大了22的绿色部分之后增加的合法矩阵的面积和是多少。
计算高度为h1+1：
宽度为x*1的矩阵可以得到：

宽度	数量
1	x
2	x-1
……	……
x	1

所以总宽度为
$∑i=1xi∗(x−i+1)\sum_{i=1}^x{i*(x-i+1)}$
$=∑i=1xx∗i−∑i=1xi2+∑i=1xi==\sum_{i=1}^x{x*i}-\sum_{i=1}^x{i^2}+\sum_{i=1}^x{i}=$
$∵∑i=1xi2=x(x+1)(x∗2+1)6\because \sum_{i=1}^x{i^2}=\frac{x(x+1)(x*2+1)}{6}$
$∴\therefore$ 原式 $=x(x+1)(x+2)6=\frac{x(x+1)(x+2)}{6}$
高度从h1+1到h2
所以增加的总面积为
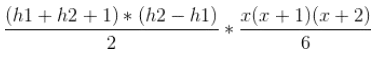
在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
#define ll long long

const int N = 2e3+10;

ll d[N][N];
char s[N];

struct node{
    ll h,index;
}a[N];

int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    for (int i = 1;i<=n;i++)
    {
        scanf("%s",s+1);
        for (int j = 1;j<=m;j++)
        {
            if (s[j] == '.') d[i][j] = d[i-1][j] + 1;
        }
    }
    ll ans = 0;
    for (int i = 1;i<=n;i++)
    {
        int len = 0;
        memset(a,0,sizeof(a));
        for (int j = 1;j<=m;j++)
        {
            int last = j;
            while (len > 0 && a[len].h > d[i][j])
            {
                ll x = j-a[len].index,h1 = max(d[i][j],a[len-1].h),h2 = a[len].h;
                last = a[len].index;
                ans += x * (x + 1) * (x + 2) / 6 * (h2 - h1) * (h1 + h2 + 1) / 2;
                len--;
            }
            if (d[i][j] == a[len].h) continue;
            a[++len].h = d[i][j];
            a[len].index = last;
        }
        while (len > 0)
        {
            ll x = m-a[len].index + 1,h1 = a[len-1].h,h2 = a[len].h;
            ans += x * (x + 1) * (x + 2) / 6 * (h2 - h1) * (h1 + h2 + 1) / 2;
            len--;
        }
    }
    cout<<ans;
    return 0;
}