2019 ICPC 银川区域赛 H - Delivery Route

2019 ICPC 银川区域赛 H - Delivery Route

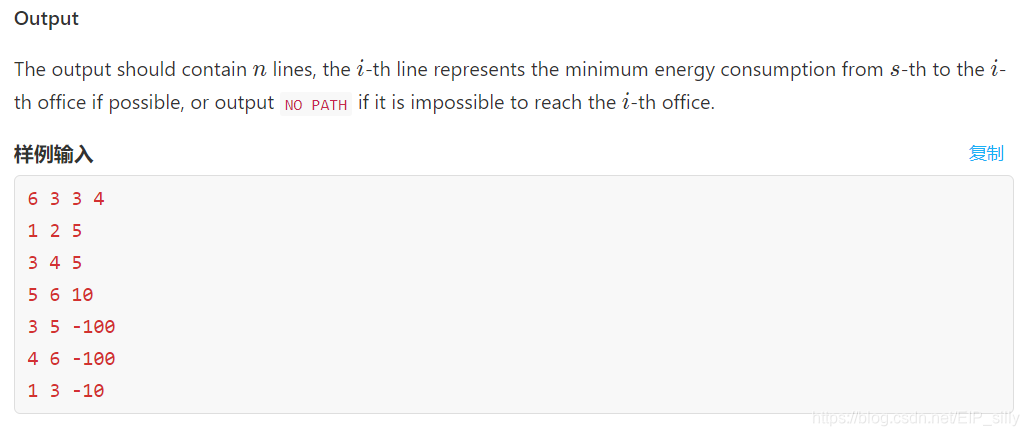
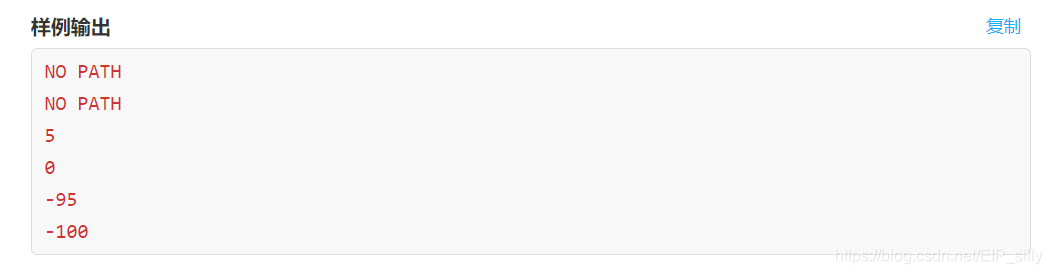
给一个n个点,x条双向边，y条单向边的图，同时双向边权全为正，单向边权有可能为负，且保证单向边不会出现在环中。求从点s分别到1~ n的最短距离。

打重现赛的时候想到了 tarjan强联通缩点，内部dijkstra，外部拓扑排序来解决。
但是觉得自己图论太菜了，就和队友一起去做A题的DP
事实证明，就算是赛后补题还是花了我大半天的时候才调对

不说了，是一道好题，直接上代码，讲解代码

#include<bits/stdc++.h>
using namespace std;
#define PII pair<int,int>

const int MAXN = 25e3+10;
const int inf = 2147483647;

struct node{
    int u,v,w,nx;
    bool operator < (const node &x) const 
    {
        return u == x.u ? v < x.v : u < x.u;
    }
    bool operator == (const node &x) const
    {
        return (u == x.u &&  v ==  x.v);
    }
};

struct EDGE{
    node e[150010];
    int head[MAXN],tot;
    void add(int u,int v,int w)
    {
        e[++tot].u = u;
        e[tot].v = v;
        e[tot].w = w;
        e[tot].nx = head[u];
        head[u] = tot;
    }
}edge1,edge2,tmp;
//edge1用来存原图，跑tarjan缩点
//edge2用来存缩点后的图，用来跑拓扑排序

int in[MAXN],dis[MAXN];

int low[MAXN],dfn[MAXN],s[MAXN],slen,scnt,col[MAXN],vis[MAXN],num;

vector<int> g[MAXN],m[MAXN];

void tarjan(int u)
{
    dfn[u] = low[u] = ++num;
    s[++slen] = u;
    vis[u] = 1;
    for (int i = edge1.head[u];i;i = edge1.e[i].nx)
    {
        int v = edge1.e[i].v;
        if (!dfn[v])
        {
            tarjan(v);
            low[u] = min(low[u],low[v]);
        }
        else if (vis[v]) low[u]=min(low[u],dfn[v]);
    }
    if (dfn[u] == low[u])
    {
        scnt++;
        do
        {
            m[scnt].push_back(s[slen]);//记录下每个强联通内有哪些点
            vis[s[slen]] = 0;
            col[s[slen]] = scnt;//记录每个点属于哪个强连通块
        } while (s[slen--] != u);
    }
}

void dij(int s) {
	priority_queue<PII,vector<PII>,greater<PII>> q;
    bool check[MAXN] = {};
	q.push(PII(dis[s],s));
	while (!q.empty())
	{
		int d = q.top().first;
		int u = q.top().second;
		q.pop();
		if (check[u] || d > dis[u]) continue;
        check[u] = 1;
		for (int i = edge1.head[u];i;i = edge1.e[i].nx)
		{
            PII y(d+edge1.e[i].w,edge1.e[i].v);
            //如果v和s不属于同一个连通块 或者 v已经访问过 就跳过
            if (col[y.second] != col[s] || check[y.second]) continue;
			if (dis[y.second]>y.first)
			{
				dis[y.second] = y.first;
				q.push(y);
			}
		}
	}
}

queue<int> q;

void update(int last)
{
    //连通块内部的每个点都跑一遍，更新到其他连通块的起始点的距离
    for (int i = 0;i<m[col[last]].size();i++)
    {
        int u = m[col[last]][i];
        for (int j = edge1.head[u];j;j = edge1.e[j].nx)
        {
            int v = edge1.e[j].v;
            if (col[v] == col[last]) continue;
            dis[v] = min(dis[u] + edge1.e[j].w,dis[v]);
        }
    }
    //更新相关连通块的入度，就是跑拓扑排序
    for (int i = edge2.head[col[last]];i;i = edge2.e[i].nx)
    {
        in[edge2.e[i].v]--;
        if (in[edge2.e[i].v] == 0)
        {
            //把连通块的起始点加入到队列当中
            for (int j = 0;j<g[edge2.e[i].v].size();j++)
                q.push(g[edge2.e[i].v][j]);
        }
    }
}

int main()
{
    int n,x,y,s;
    scanf("%d%d%d%d",&n,&x,&y,&s);
    for (int i = 1,u,v,w;i<=x;i++)
    {
        scanf("%d%d%d",&u,&v,&w);
        edge1.add(u,v,w);
        edge1.add(v,u,w);
    }
    for (int i = 1,u,v,w;i<=y;i++)
    {
        scanf("%d%d%d",&u,&v,&w);
        edge1.add(u,v,w);
    }
    tarjan(s);//tarjan缩点

    //缩点建图，用来后面跑拓扑排序。
    int len = 0;
    for (int i = 1;i<=edge1.tot;i++)
    {
        //如果这条边的两个端点，存在一个是无法到达的 或者 两个端点属于同一个连通块
        if (col[edge1.e[i].u] == 0 || (col[edge1.e[i].v] == col[edge1.e[i].u]) || col[edge1.e[i].v] == 0) continue;
        //记录下每个 连通块中哪些点 其他是连通块指向它的
        //这些点就是后面跑dij时候的起始点
        g[col[edge1.e[i].v]].push_back(edge1.e[i].v);
        len++;
        tmp.e[len].u = col[edge1.e[i].u];
        tmp.e[len].v = col[edge1.e[i].v];//重新建图
    }
    sort(tmp.e+1,tmp.e+1+len);
    int pos = unique(tmp.e+1,tmp.e+len+1) - tmp.e - 1;//去除相同边

    for (int i = 1;i<=pos;i++)
    {
        edge2.add(tmp.e[i].u,tmp.e[i].v,tmp.e[i].w);//缩点后建图
        in[tmp.e[i].v]++;//记录每个连通块的入度
    }
    for (int i = 1;i<=n;i++ ) dis[i] = inf;
    dis[s] = 0;
    q.push(s);
    int u;
    while (!q.empty())
    {
        u = q.front();
        q.pop();
        dij(u);//连通块内部跑dij
        //如果连通块内的起始点都跑完了。就更新相关连通块的入度，把入度为0的连通块的起始点加进队列
        if (q.size() == 0 || col[q.front()] != col[u]) update(u);
    }
    for (int i = 1;i<=n;i++)
    {
        if (dis[i] == inf) printf("NO PATH\n");
        else printf("%d\n",dis[i]);
    }
    return 0;
}