8.7欧几里得算法与拓展欧几里得算法

欧几里得算法

欧几里得算法就是小学生都会我们所熟知，求最大公约数的辗转相除法。

int gcd(int a,int b)
{
	if(b==0) return a;
	else returngcd(b,a%b);
}

---

拓展欧几里得算法

在学习拓展欧几里得之前，要了解一些基本概念。
别人我不知道，反正我没学o.0

---

同余

同余式是数论的基本概念之一，设m是给定的一个正整数，a、b是整数，若满足m|(a-b)，则称a与b对模m同余，记为a≡b(mod m)，或记为a≡b(m)。
通俗理解↓：
数a被m整除时，得到唯一的商$q_1$与余数r；
数b被m整除时，得到唯一的商$q_2$与余数r。
a与b的余数相同，则a与b同余。

---

逆元

同余这件事儿是不满足除法的，即
a/b mod p != (a mod p)/(b mod p)
某位聪明的数学家看着不爽为了便于计算，引入了逆元的概念。
b的逆元x，即使 b·x ≡1(mod p)。

接下来进行数学变换：
设a/b = k, 则 a/b = k(mod p)
两边同乘bx：
a/b * bx ≡ k * 1 (mod p)
化简：
ax ≡ k (mod p)。

---

费马小定理

a的p-1次方 ≡ 1 （mod p)。
若p为质数，可以发现：
a·a的p-2次方 ≡ 1(modp)。

---

拓展欧几里得算法

这是一个数学式与递推式的计算，用于计算二元一次方程的整数解。
过程比较繁杂。等不及直接拖进度条到结尾。

两解之间的关系

由开篇的辗转相除可以得到，ax + by = gcd(b, a%b)。记住这个式子！

当b=0时，gcd(a, b) = a。此时x = 1，y = 0为一组解。

当b≠0时。设
$a{x}_1+b{y}_1=gcd(a,b)$
再由辗转相除法可以得到，gcd(a,b) = gcd(b,a %b)
设
$b{x}_2+(a$%b$)y_2$ = gcd(b, a%b) = gcd(a,b)
则
$b{x}_2+(a$%b$)y_2$ = $a{x}_1$ + $b{y}_1$。

接下来，翻回上面的逆元的推导公式
将a%b = a-(a/b)*b
代入
$b{x}_2+(a$%b$)y_2$ = $a{x}_1$ + $b{y}_1$ 自己拿纸算一下
得到

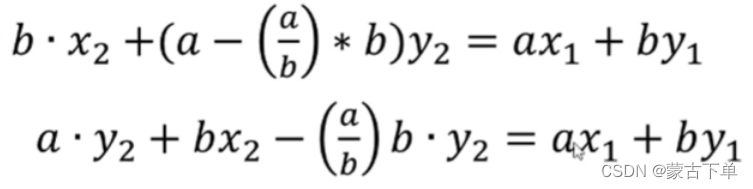
键盘实在不能再敲了呃啊好麻烦（小声）

那么知道$x_2$,$y_2$后，推出
$x_1$ = $y_2$
$y_1$ = $x_2$ - (a/b) * $y_2$ 这就是解之间的关系。

现在我们推出了关系式，接下来考虑边界条件
其实前面已经写过了！
当b=0时，gcd(a, b) = a。此时x = 1，y = 0为一组解。

核心代码

int x, y;
int exgcd(int a, int b){
    if(b == 0){
        x = 1; 
        y = 0;
        return a;
    }
    int d = exgcd(b, a%b);
    int t = y;
    y = x - a/b*y;
    x = t; 
    return d;
}

如果ax+by=是gcd(a,b)的倍数，则该式有解。

计算通解

上述过程只计算出了一种解，那么……如何计算其他解？

设
a$x_0$ + b$y_0$ = gcd(a, b)
得出
a($x_0$k) + b($y_0$k) = k* gcd(a, b)

因此，我们计算出通解;

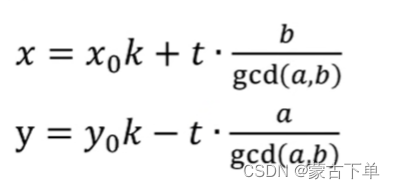
其中，t为常数。
由于推导过程实在太难打字了，直接说一系列加减乘除后的结论：
a与b互质
{x= $x_0$k + t * b, y= $y_0$k - t * a}。

计算最小正整数解

根据通解的格式推出，每第b次循环，最小解都为$x_0$%b。但x有可能是负数，所以要让x再加上b，最后让这一堆数对b取余。
所以，($x_0$%b + b)%b 为二元一次方程的最小正整数解。

核心代码

void exgcd(ll a,ll b,ll &x,ll &y){
	if(b == 0){
		x = 1;
		y = 0;
		return;
	} 
	exgcd(b, a%b, y, x);
	y -= a/b*x;
}
	
int main(){
	int a, b, x, y;
	cin >> a >> b;
	exgcd(a, b, x, y); 
	cout << (x%b+b)%b;
	return 0;
}

尊嘟好难。。。。我学了整整一个半小时