KMP匹配算法概念+实例

原创已于 2023-02-16 20:28:27 修改 · 823 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构

于 2022-10-23 15:06:01 首次发布

打基础专栏收录该内容

23 篇文章

订阅专栏

本文详细介绍了KMP算法中常见的两种next数组构造方法，包括经典模式串匹配失败后的跳转规则，并通过实例演示了如何计算next数组。两种next数组的区别在于处理匹配失败时的不同策略，有助于理解KMP算法的工作原理。

此文重点梳理两种最常见的next数组，以及在KMP匹配中的应用

符号说明

$模式串:T[i]i=1,...,T_length主串:S[i]i=1,...,S_lengthnext数组:next[i]i=1,...,T_length 模式串:T[i] \quad i=1,...,T\_length\\ 主串:S[i] \quad i=1,...,S\_length\\ next数组:next[i]\quad i=1,...,T\_length\\$

第一种next数组

第一种next数组在KMP中的作用为：
当S[i]与T[j]在主串 $S [i]$ 处匹配失败时，将指向模式串的指针 $j$ 跳转到模式串的 $n e x t [j]$ 处
$next[j]=\begin{cases} 0 &当j=1时\\ Max\{k|1<k<j且“T_1 \cdots T_{k-1}”=“T_{j-k-1}\cdots T_{j-1}”\} &当此集合不为空时\\ 1 &其他情况\\ \end{cases}$
例1.T="aba"时next数组的计算过程

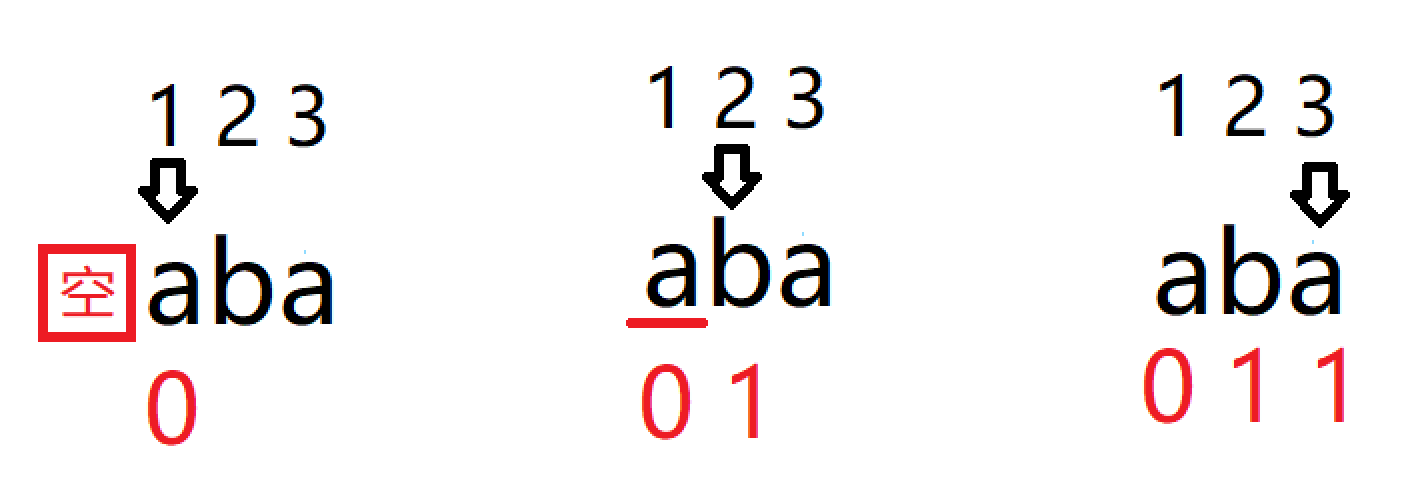
例2.T="abaabcac"时next数组的计算过程
由于aba在上例中已计算过，从j=4开始

通过两个例子，可以将next数组的公式总结为：

j=1时，nextj]=0成立
当j $≠\neq$ 1时，扫描1~j-1，得到最长前后缀长度;next[j]=最长前后缀长度+1
(若无相等，则前后缀长度为0，next[j]=1。如例2中j=7时)
注意：前缀和后缀可重叠

练习1.
求abababaab的next数组

011234562

代码实现

void get_next(int T_length) {//模式串next数组的生成
	int i = 1, j = 0;
	next[1] = 0;
	while (i <= T_length) {
		if (j == 0 || T[i] == T[j]) {
			i++;
			j++;
			next[i] = j;
		} else
			j = next[j];
	}
}

在KMP中的应用

int  Index_KMP(int S_length, int T_length, int pos) {//从pos开始的一次KMP匹配
	int i = pos, j = 1;
	while (i <= S_length && j <= T_length) {
		if (j == 0 || S[i] == T[j]) {
			i++;
			j++;
		} else
			j = next[j];
	}
	if (j > T_length) {
		printf("%d ", i - T_length);
		return i - T_length;
	} else return 0;//若匹配失败
}

第二种next数组

第一中next数组在KMP中的作用为：
当S[i]与T[j]匹配失败时，查询前一位 j-1 的next[j-1]，跳过next[j-1]个数，从next[j-1]+1的位置开始重新匹配。
$next[j]=\begin{cases} 0 &当j=1时\\ Max\{k|1<k<j且“T_1 \cdots T_{k}”=“T_{j-k+1}\cdots T_{j}”\} &当此集合不为空时\\ 0&其他情况\\ \end{cases}$
例3.T="aba"时next数组的计算过程

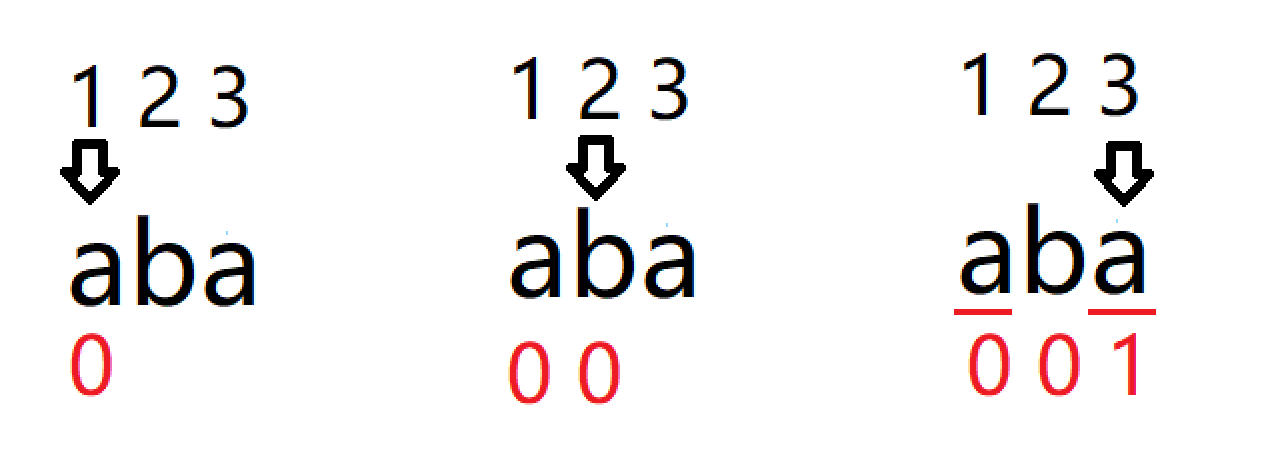
例4.T="abaabcac"时next数组的计算过程
由于aba在上例中已计算过，从j=4开始

通过两个例子，可以将next数组的公式总结为：

j=1时，nextj]=0成立
当j $≠\neq$ 1时，扫描1~j，得到最长前后缀长度;next[j]=最长前后缀长度
(若无相等，则前后缀长度为0，next[j]=0。如例4中j=7时)

代码实现

void get_next(int T_length) {//模式串next数组的生成
	int i = 2, j = 1;
	next[1] = 0;
	while (i <= T_length) {
		if(j==1&&T[i]!=T[j]){
			next[i]=0;
			i++;
		}
		if ( T[i] == T[j]) {
			next[i] = j;
			i++;
			j++;
		} else {
			j = next[j-1] + 1;
		}
	}
}

在KMP中的应用

int  Index_KMP(int S_length, int T_length, int pos) {//从pos开始的一次KMP匹配
	int i = pos, j = 1;
	while (i <= S_length && j <= T_length) {
		if(j==1&&S[i]!=T[j]){
			i++;
		}
		if (S[i] == T[j]) {
			i++;
			j++;
		} else {
			j = next[j-1] + 1;
		}
	}
	if (j > T_length) {
		printf("%d ", i - T_length - 1);
		return i - T_length;
	} else return 0;//若匹配失败
}

完整实现：
一:

#include<bits\stdc++.h>
#define MaxSize 10000
char T[MaxSize], S[MaxSize];
int next[MaxSize];
void get_next(int T_length) {//模式串next数组的生成
	int i = 1, j = 0;
	next[1] = 0;
	while (i <= T_length) {
		if (j == 0 || T[i] == T[j]) {
			i++;
			j++;
			next[i] = j;
		} else
			j = next[j];
	}
}
int  Index_KMP(int S_length, int T_length, int pos) {//从pos开始的一次KMP匹配
	int i = pos, j = 1;
	while (i <= S_length && j <= T_length) {
		if (j == 0 || S[i] == T[j]) {
			i++;
			j++;
		} else
			j = next[j];
	}
	if (j > T_length) {
		printf("%d ", i - T_length);
		return i - T_length;
	} else return 0;//若匹配失败
}
int main() {
	int i;
	int S_length ;//主串
	int T_length ;//模式串
	
	scanf("%d", &T_length);
	scanf("%s", T + 1);
	scanf("%d", &S_length);
	scanf("%s", S + 1);

	get_next(T_length);

	for (int position = 1; position < S_length; position++ ) {
		position = Index_KMP(S_length, T_length, position);
		if (position == 0)
			break;
	}
	/*for (i = 1; i <= T_length-1; i++)//输出next数组
		printf("%d ", next[i]);
	printf("%d", next[i]);*/
	return 0;
}

二:

#include<bits\stdc++.h>
#define MaxSize 10000
char T[MaxSize], S[MaxSize];
int next[MaxSize];
void get_next(int T_length) {//模式串next数组的生成
	int i = 2, j = 1;
	next[1] = 0;
	while (i <= T_length) {
		if(j==1&&T[i]!=T[j]){
			next[i]=0;
			i++;
		}
		if ( T[i] == T[j]) {
			next[i] = j;
			i++;
			j++;
		} else {
			j = next[j-1] + 1;
		}
	}
}
int  Index_KMP(int S_length, int T_length, int pos) {//从pos开始的一次KMP匹配
	int i = pos, j = 1;
	while (i <= S_length && j <= T_length) {
		if(j==1&&S[i]!=T[j]){
			i++;
		}
		if (S[i] == T[j]) {
			i++;
			j++;
		} else {
			j = next[j-1] + 1;
		}
	}
	if (j > T_length) {
		printf("%d ", i - T_length - 1);
		return i - T_length;
	} else return 0;//若匹配失败
}
int main() {
	int i;
	int S_length ;//主串
	int T_length ;//模式串

	scanf("%d", &T_length);
	scanf("%s", T + 1);
	scanf("%d", &S_length);
	scanf("%s", S + 1);

	get_next(T_length);

	for (int position = 1; position < S_length; position++ ) {
		position = Index_KMP(S_length, T_length, position);
		if (position == 0)
			break;
	}
	/*printf("\n");
	for (i = 1; i <= T_length - 1; i++) //输出next数组
		printf("%d ", next[i]);
	printf("%d", next[i]);*/
	return 0;
}