从懂到用(2)：讲一些别人不细讲的BN关键点

本文链接：https://blog.youkuaiyun.com/Duke_Rodriguez/article/details/126415380

本文详细解析BatchNormalization（BN）的内部协变量移位问题，通过归一化解决网络训练过程中的分布不稳定性，提升收敛速度。讲解了BN的工作原理、优点（如更快收敛、防止过拟合）、使用方法及PyTorch实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前言

之前我发了一篇文章，是讲ResNet的，里面的网络结构有BN层，但当时我们没有细讲，所以今天我们来讲讲Batch Normalization，简称BN。BN的概念来自这篇论文：《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》，下面我们从为什么要使用BN开始，一直讲到如何使用。

这里需要说明的是，在写这篇文章时，我发现很多博主对为何要使用γ和β进行变换重构这件事几笔带过，没有讲清讲透，导致包括之前的我在内的很多人对BN层的合理性造成了一定的误解。所以今天我会讲讲我现在的个人理解，希望对你有启发。

内部协变量移位

众所周知，深度学习其实是在学习数据的一种分布，当学习出来的分布和实际的分布很相似时，那么我们的网络效果就很好。需要注意的时，我说的分布相似是指这个分布的形状、胖瘦和位置都差不多（请记住这点，因为后面要继续提到）。形状是指这个分布的曲线图，如下面分别是正态分布和指数分布的图，可以看出他们长得不一样。

图片来自网络

胖瘦是指这个形状差不多，但是方差不同，表现出来的些许变形，如下图。

图片来自网络

而位置不同则是因为期望不同，整个形状在数轴上移动了。

我们再细化上面的说法：假设我们有一个三层网络。一开始我们的输入其实符合某种分布，然后经过第一层后，第一层的输入（第二层的输入）又符合另外一种分布，第二层结束后，其输出又满足另外的另外一种分布。也就是说，每层的输出都有自己的一种分布，且这个输出分布是和它的输入分布有关的。

那如果，我前面第一层的输出分布发生了变化，由于连锁反应，会影响第二层，第二层影响第三层……第N层，可以说是牵一发而动全身。如果我们的层数太深，这种反应结果是非常恐怖的，大家可以想想蝴蝶效应。这种情况就是内部协变量移位了。

出现这种问题时，前面动一下，后面就变动巨大，那么一开始学到的参数就不再适用了，网络又要重新适应新的分布了。这样一来二去，网络收敛的时间就很久，甚至层数过深可能不收敛。

为了解决这个问题，前人采用较小的学习率，希望它能够慢慢动，不至于地动山摇。但这个方法带来的副作用不小，学习率太低拟合速度进一步变久，而且网络层数过深时还是难以避免出现内部协变量移位。

解决办法

那这个问题如何解决呢？一个思路是我使每一层的输入都稳定，那不就行了吗？因此论文作者想到了归一化。所谓归一化就是把数据映射到0-1之间。比较好的方法是使用白化。使用了白化后，能让特征之间的相关性减小，同时让特征具有相同的方差。但你听它这个效果也知道，它里面包含了降维的操作。实际也确实如此，白化里使用了PCA降维，如果网络使用白化操作的话，计算量很大，而且不是处处可微。

白化虽然效果好，但显然不适合使用在网络种，单单一条计算量很大就足够治死罪了。所以作者受到白化的启发，搞了一个新的办法。新方法舍弃了白化优点中的让特征之间相关性减少这一点，只取另外一个优点。这个方法就是Batch Normalization，算法如下。

图片来自论文

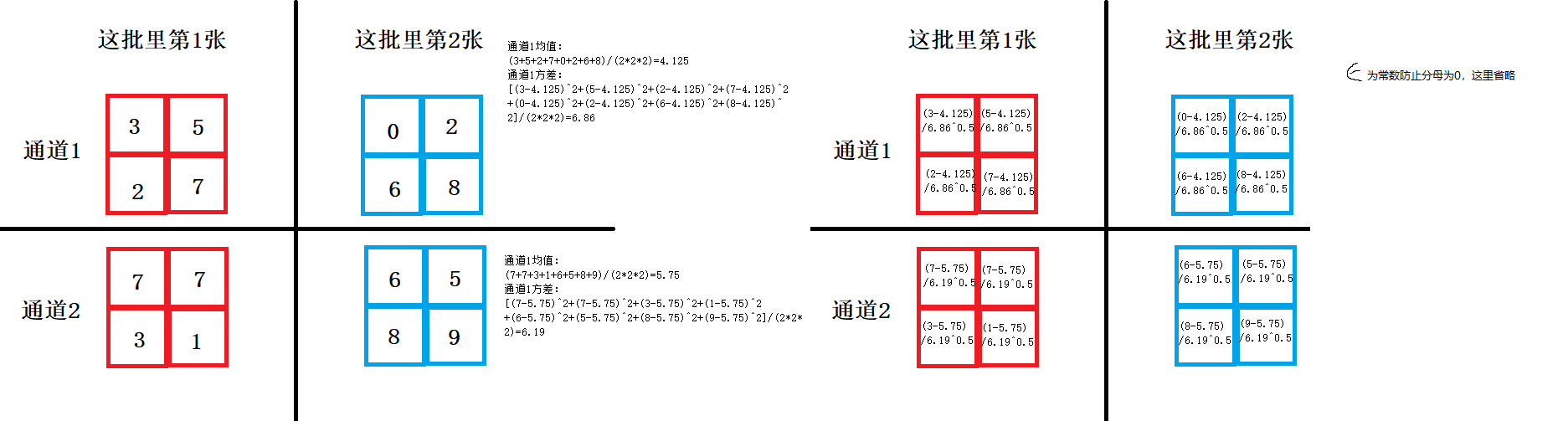
首先讲一下这个计算流程。我们将数据集分批，比如数据集有256张图像，我们分成4批，那就是每批64张图片。然后我们送一批进去网络训练，到BN层的时候，我们再进行上图算法的计算。但我们上图中的x是指图像中的什么呢？由于我们输入的是图像，因此我们假设我们在进行图像分类任务，而BN层的输入是卷积层的输出，也就是特征图，它的矩阵形状应该是这样的：[64,C,W,H]

64就是这一批的大小，也就是我们常说的batch_size啦，而C是指通道数，W和H就是图像的长和宽。那么这个x其实是指每个通道上的每个像素点所存储的值。

我们可以看到这个算法首先要算平均数和方差，那么我们是把所有像素值都加起来算吗？其实不是的。应该是每个通道的加起来算。比如说我们有8个通道，也就是有64*8张特征图，也就是[64,8,W,H]，那么我们应该要算8组平均数和方差。也就是把64张图像每张的同一个通道抽出来，然后把所有像素值抽出来算。

计算出平均数和方差后，我们再遍历每一个像素，根据上图第三个式子计算出新值进行更新，然后依然是遍历每一个像素，让它乘一个γ再加一个β，再次更新这个新值。大家结合我说的，再看看下图，应该就能明白了。

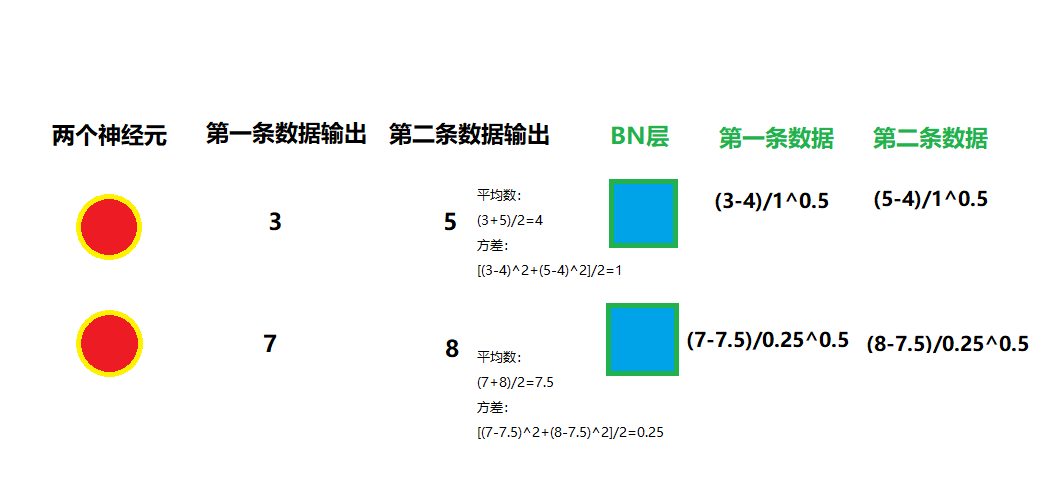
那如果是全连接层呢？全连接层的输入应该是[64,1000]，64是指这批数据集有64条数据，和上面的64是一样的。然后1000是指这个全连接层有1000个神经元。根据这个算法，我们是要算1000组的平均数和方差。64条数据在第n个神经元的输出搞在一起计算。

算法理解

讲完计算，我们来讲讲怎么理解这个算法。首先上面算法的式子其实就是归一化的过程，将数据全部弄到期望为0，方差为1的分布。你可能会问，如果全部都弄到这个分布，那之前的层学习这么多还有个鬼用，反正都要变成这个分布的。实则不然，其实你默认地认为只要期望和方差相同，那它就是相同的分布，可能你脑海中已经浮现出标准正态分布的图像了。

但其实，归一化后，这个分布的形状并没有变（对形状的定义参考我上面说的），只是把胖瘦限制了，位置限制了。我的理解是，训练就像一个很木讷的人在玩橡皮泥，他只会在一个固定的地方玩，如果你把橡皮泥的位置挪到旁边很多，或者把这个橡皮泥压胖（基本形状不变），那么这个人它就整不会了，它就只能推倒重做了。而每层都归一化，就相当于把这个胖瘦和位置归位，让这人可以继续上次结果继续做。

但是，如果期望为0，方差为1，那么就限制了数据的范围了，比如它只能使用激活函数的中间那部分，就会限制激活函数的表达。因此我们使用β和γ，将这个分布的位置和胖瘦变大一点，能让它使用激活函数更多的范围，算是补偿了一些非线性的表达。

你可能会说，这样不也改变了分布的位置和胖瘦吗，那那个木讷的人怎么办，他可能又找不到它的橡皮泥了。其实这个变换重构的操作相当于告诉了木讷的人，以后我们改去这里玩，你的橡皮泥会变胖一点。

举个实体的例子，假如你有两个网络，其中一个网络是三层卷积层，如果你第一层参数发生变化，分布向左走了，然后经过第二层，又向左走了，第三层的输入就会向左走了好多，第三层又得重新适应分布。而另外一个网络，三层卷积层，每层之间都有一个BN层。那么第一层参数改变，分布向左走了，到了BN层，先给你归一化拉回中间，然后再用变换重构，让这个分布偏左一点。因为BN层这里的变换重构告诉了后面的层要到偏左一点找，所以第二个卷积层的输入很容易找到。随后第二个卷积层使分布往左走了，到了下一个BN层又给你拉回来。因此虽然第一层发生了变动，但后面的BN层都给你拉回来，不让你跑偏，所以后面的层只需要专注于改分布形状就行，完全不用担心输入跑偏。

优点

根据上面我们的说法，因此输入不会跑偏，就不用花时间重新适应输入分布，因此我们就可以使用更大的学习率，且收敛训练速度更快了。

而且由于归一化后限制了你在激活函数上的输出（你只能选取中间梯度大的部分，而不会选择旁边梯度小的地方），所以不会出现训练到深层训练不动的情况。

第三个好处就是可以防止过拟合，BN要求网络以一批数据输入网络，那么这批数据塞进来，网络会综合考虑学习，不会出现学会某个奇怪数据的奇怪特征，造成过拟合。比如你向别人请教问题，你多请教几个，综合一下他们的解释，那你大概就了解到正解。但如果你只问一个人，很可能那个教了错误的给你。由于能够防止过拟合，所以我们也能不使用Dropout了。

使用方法

假如你上面都没看懂，问题不大，你只需要知道如何使用，且记住它的优点，再知道它什么时候使用就可以了。

在Pytorch里我们这么使用它：

self.bn1=nn.BatchNorm2d(channels)  # channels是输入特征图的通道数

至于什么时候使用，我们是在卷积层或者全连接层后紧挨着使用，随后在激活函数前使用。一般是卷积层＋BN层＋激活函数。

还有一点是，当网络训练完，要进行使用时，我们是一张一张地塞进去的，此时已经没有批这个概念了，那我们如何求平均值和方差呢？这里我们说说Pytorch里BN层的做法。在Pytorch里使用的是滑动平均计算法。将训练时每一批数据计算到的均值和方差累计起来。当要使用时，则使用这两个累计值进行计算。

moving_mean = moving_mean * momentum + batch_mean * (1 - momentum)
moving_var = moving_var * momentum + batch_var * (1 - momentum)

其中momentum是动量，默认0.9。而batch_mean和batch_var就是每一批计算的方差和均值。

作者：公|众|号【荣仙翁】

内容同步在其中，想看更多内容可以关注我哦。