从懂到用（1）：卷积与池化

最新推荐文章于 2024-08-24 11:11:43 发布

玮爵爷～

最新推荐文章于 2024-08-24 11:11:43 发布

阅读量1.6k

点赞数 6

分类专栏：从懂到用文章标签：人工智能深度学习机器学习分类 pytorch

本文链接：https://blog.youkuaiyun.com/Duke_Rodriguez/article/details/126286567

版权

从懂到用专栏收录该内容

2 篇文章

订阅专栏

前言

在图像识别的任务上，我们通常会使用到卷积层和池化层，那么卷积和池化的具体计算过程是如何的呢？相关的名词概念是什么意思呢？在代码上要如何实现呢？下面我们将回答这几个问题，最后用Pytorch进行代码实现。

图像的组成

卷积和池化一般是在图像上进行操作的，所以我们有必要将图像的组成讲清楚。

首先我们平时拍出来的图像大多是有若干个像素组成，比如有的图像的分辨率是28*28，那么它就是有28*28个像素组成。每个像素我们可以理解为一个小格子，我们在每个格子里涂上不同的颜色，就能形成一张色彩丰富的图片。

假设格子数够多，这图像就越有高清的感觉，因为它足够的细腻。假如我给你三个格子来表示脸，那你最多只能涂三种颜色。但如果我给你成千上万个格子表示脸，脸上每个细节你都能画出来。

图片来自网络

上述只是我们在直观上理解，那么计算机上如何表示呢？

按照我们刚才分析的，我们只需要记录每一个格子的位置和它所存储的颜色便可以了。计算机使用矩阵来解决这个问题，我们可以把矩阵看成一个方阵。大家上学时都做过广播体操吧？所有同学排成几行几列的方阵。我们的矩阵就像这个方阵，行数和列数与图片的尺寸一样，当我们需要知道第三行第五列这个像素的数值，我们只需要访问矩阵里同样位置所存储的数据便可以了。

解决了格子位置的问题，我们还要考虑如何表示所存储的颜色。众所周知，我们的色彩可以使用三原色组合而成，我们可以用三原色混合出所有的颜色，我们只需要控制三种颜色的比例便可以了。计算机也是如此操作的，只不过我们在图像处理中用的三原色是红色（RED）、绿色（GREEN）和蓝色（BLUE），也就是我们熟知的RGB，如果学过PS的肯定了解这个。

我们用三组0~225来表示这个颜色使用的程度，越靠近225，使用的颜色就越深，越靠近0，使用的颜色就越浅。

图片来自网络

知道格子位置与颜色深度的表示，下面我们来讲讲常见的两种存储方式。第一种就是只有一个矩阵，每个格子里按顺序存储三组颜色数据。第二种方法是使用三个矩阵，每个矩阵掌控一种颜色，矩阵里每个格子就存储一个数字。我们可以把每个矩阵称为一个通道，我们有三个矩阵，那么就有三个通道了。

当然我们还可以多给它加几个通道，记录更多数据，比如这个点的深度或者其他信息。如果我们要表示黑白灰照片，可以只使用一个通道。通常单通道图像都是灰度图，三通道图像都是彩色图，四个通道的图像一般是通过深度相机获取的。

卷积

卷积的过程其实就是一个小框框扫描整张图，如下图：

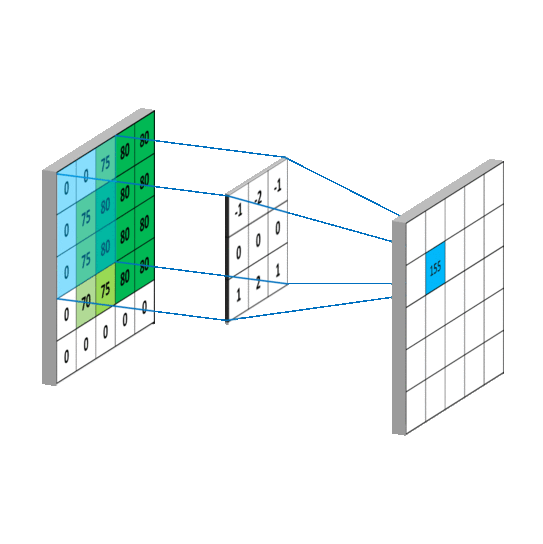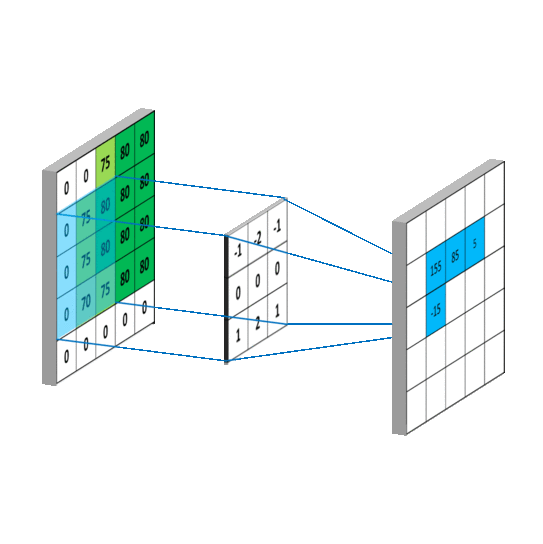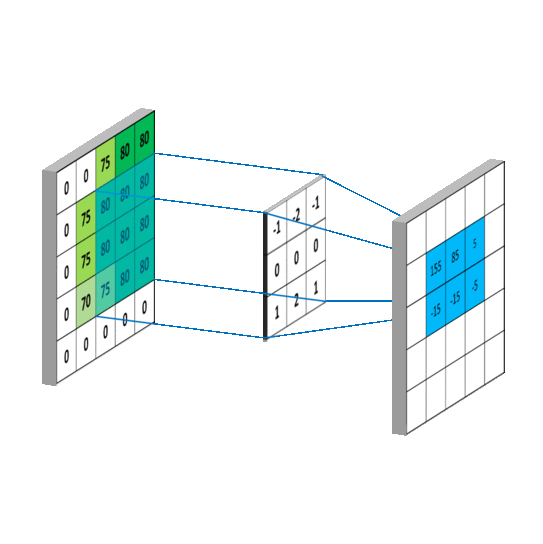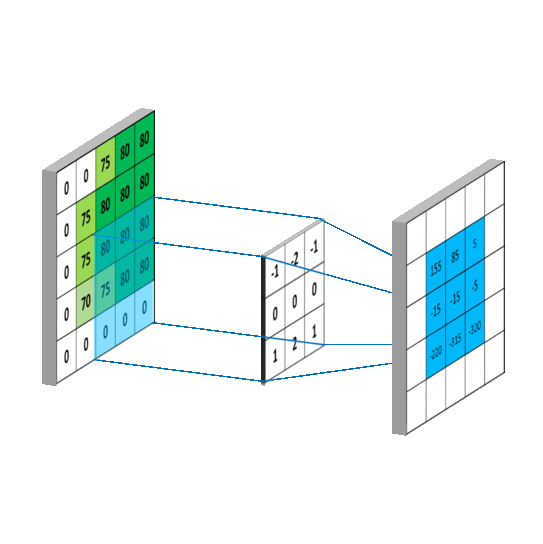
图片来自网络

我们可以把这个框框叫卷积核（kernel_size），它是一个正方形的框框，它可以是3*3、5*5、7*7或者你设定的其他尺寸。

每次扫描时我们做如下的计算，卷积核上每个数字乘上被扫描区域对应位置的数字，然后加在一起。

图片来自网络

那么在扫描时，卷积核每次要移动多少呢？这就要引入步长（stride）的概念。

如这张图，假设红色框框是卷积核一开始所在的位置，如果步长为1，那么它每次会移动一格，下一次便移动到黄色框所在的位置，再下一次就到了绿色框的位置。

如果步长是2，那么红色框下一次便会直接移动到绿色的区域。

这便是步长的概念，衡量框框每次移动的距离。

根据上面的图片我们可以知道，每次卷积后得到新的图片会比原来的图片更小，而且边缘的信息可能只被利用了一两次，而中间的像素被多次扫描到，会利用很多次，因此卷积对边缘的信息不太友好。为了解决这两个问题，我们可以在原图的外围补上几圈0，这个操作就叫padding。

如果补一圈，那么padding=1，补两圈的话，padding=2。

通过补0，增加了原图像尺寸，使原来的边缘信息更靠近中心，从而解决了刚才提到的两个问题。

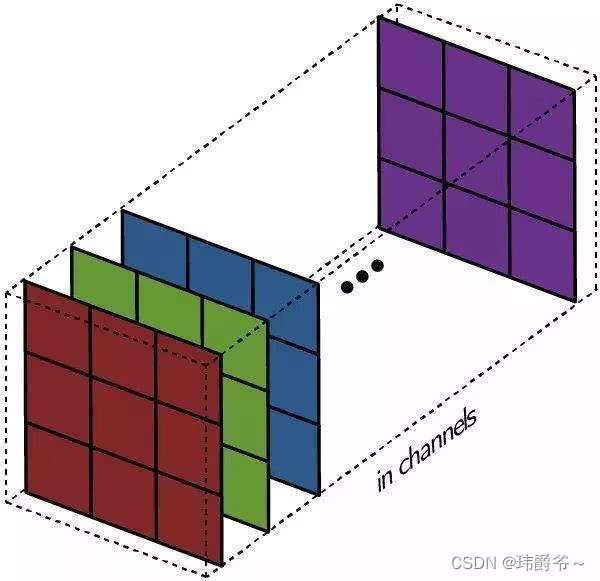
刚才说了这么久都是在一个通道上进行卷积，而我们的卷积层可能面对多个通道的图像。因此接下来我们升级到多通道卷积：

图片来自https://mlnotebook.github.io/post/CNN1/

我们可以看到原图是有三个通道，而我们有四个同样有着三通道的卷积核，经过计算后，最后我们的输出是一张四通道的图像。

而且从图中我们不难看出，每个卷积核扫描完原图后会生成一个通道的图像，四个卷积核计算完后，结果合起来才是一张四通道的图像。

我们其实可以把每个通道看成图像的一个特征，每个卷积核负责检测一个特征，那么多通道卷积就相当于，我用M个卷积核去一张有N个通道（特征）的图像上做扫描，最后得到一张有M个通道（特征）的图像。所以说卷积是一个特征提取的过程，从低维的特征中获取更高维的特征。

理解了多通道卷积的原理，那么它具体的计算过程是怎么样的呢？

图片来自网络

如这张图所描述的，其实是每个通道分别进行卷积，然后把每个通道结果上相应的位置加起来。所以卷积核的通道数是要与原图的通道数一致的。

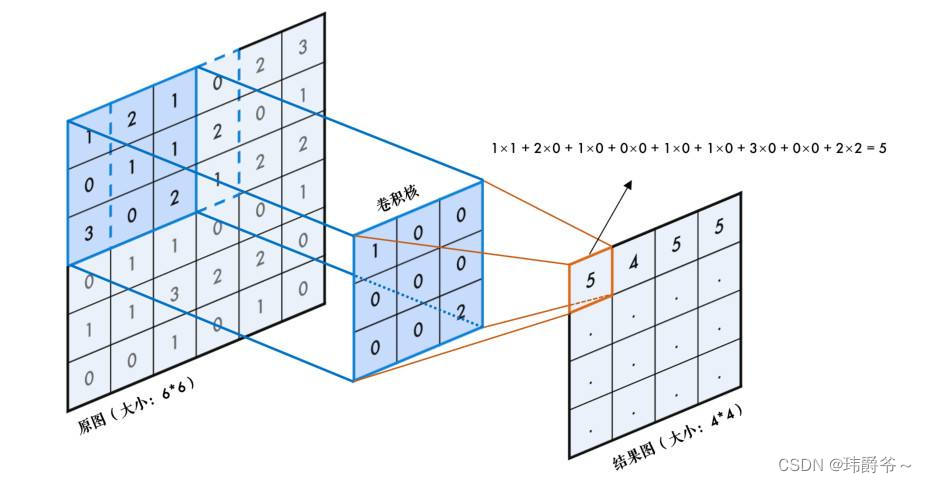
我们都知道卷积是会使图像尺寸减少的，那么我们如何计算结果图的尺寸呢？这里有一个公式：

Output_w=(original_w-kernel_size+2*padding)/stride+1

Output_h=(original_h-kernel_size+2*padding)/stride+1

其中output是输出的意思，original是原图的意思。

拿刚才的一幅图作为例子：

在这张图中，原来的图像尺寸为6*6，卷积核的尺寸是3*3，padding为1，stride为1。那么输出尺寸就是：(6-3+2*0)/1+1=4，由于长和宽都一样，因此只需要计算一次便可以了。

值得注意的是，有些论文上并没有写padding是多少，只给了个原图尺寸、卷积核尺寸、步长和结果图尺寸，所以我们需要倒推出padding是多少

池化

池化其实和卷积很像，也是一个框框在那里扫描，但计算方法不太一样。

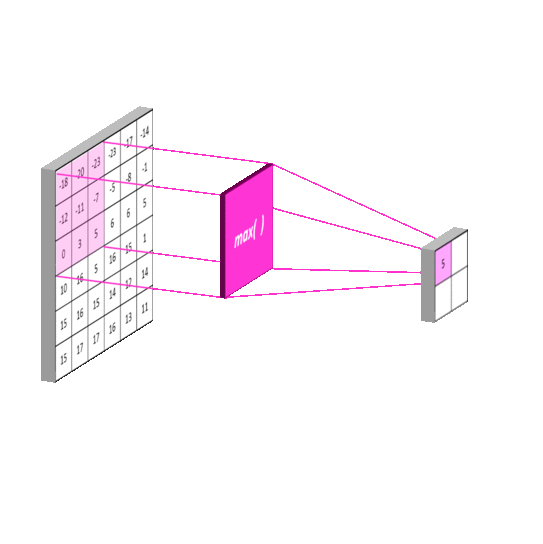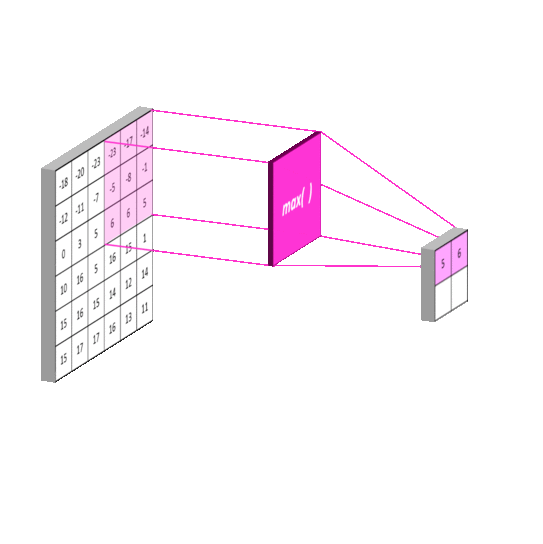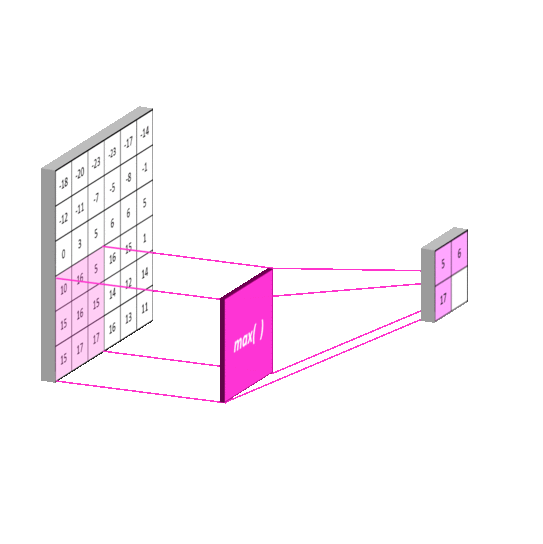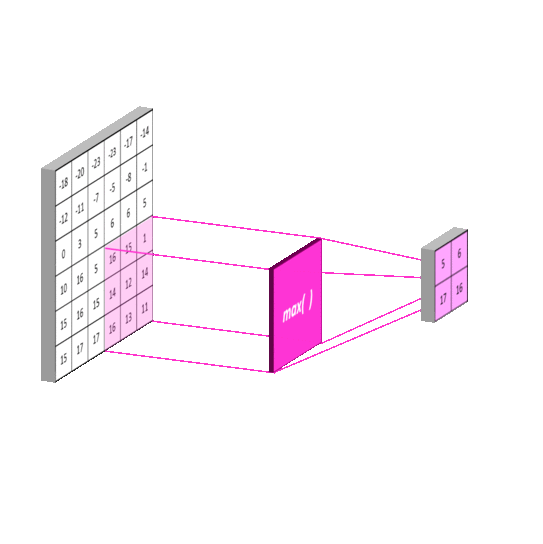
图片来自https://mlnotebook.github.io/post/CNN1/

比较常用的有平均池化和最大池化，顾名思义，就是取扫描区域里的最大值或者平均值为输出值，如下图。

值得注意的是，池化的步长一般与核的尺寸相同，也就是扫描框框不会相互覆盖。

Pytorch实战

import torch.nn as nn # 引入pytorch
conv=nn.Conv2d(in_channels=3,out_channels=8,kernel_size=3,stride=1,padding=1) # 定义层
out=conv(x) # 使用层

其中的参数：

in_channels是指原图的通道数

out_channels是指输出图的通道数

kernel_size是指卷积核尺寸

stride是指步长，默认为1

padding是补零，默认为0

还有些其他参数，用得不多，这里就不介绍了。

然后我们再实现一下池化层

import torch.nn as nn # 引入pytorch
pool=nn.MaxPool2d(kernel_size=2,stride=2) # 定义层
out=pool(x) # 使用层

kernel_size是指卷积核尺寸

stride是指步长

还有些其他参数，用得不多，这里就不介绍了。

作者：公|众|号【荣仙翁】

内容同步在其中，想看更多内容可以关注我哦。