前言
目标检测是一个常见的计算机视觉任务,在目标检测任务中,交并比作为评判检测框的标准具有很重要的意义,在实际的应用中,人们又对最初的IoU进行了诸多的改进。本文将对IoU以及他的改进形式的思路以及公式进行详细通俗的介绍。
IoU
IoU是最早的用于评价预测框与实际框差距的标准,并被用于设置关于预测框回归的损失函数,其思路就是计算预测框与实际框相交区域的面积以及相并区域的面积
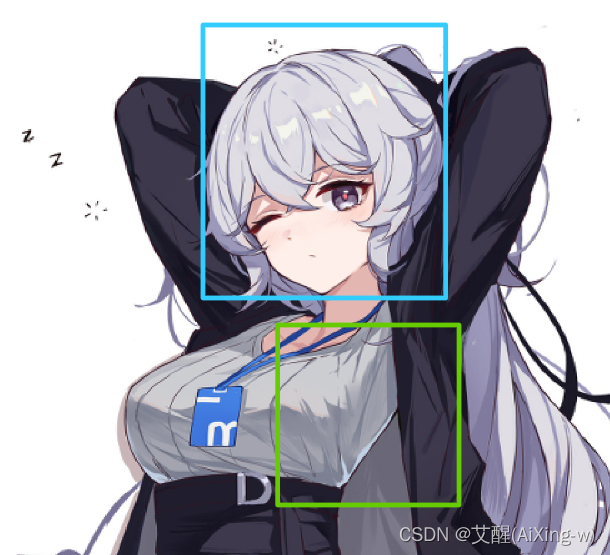
假设我们是在这样一张图片上进行目标检测

那么我们令蓝框为真实框,绿框为预测框,以这个图片的人脸检测为例介绍IoU
公式及示意图
I o U = T ∩ P T ∪ P , 其中 T 为实际框, P 为预测框 IoU=\frac{T \cap P}{T \cup P},其中T为实际框,P为预测框 IoU=T∪PT∩P,其中T为实际框,P为预测框
通俗来看

从直观上讲,就如上图,我们假设蓝框是真实框,绿框为预测框,上下红色阴影部分的面积之比就是IoU
示意图

IoU Loss
IoU越大说明真实框与预测框的重合度越高,即越好,所以我们可以使用IoU重建损失函数,一般有两种方式
I
o
U
L
o
s
s
=
1
−
I
o
U
或
I
o
U
L
o
s
s
=
−
l
n
I
o
U
IoU \space Loss =1-IoU或IoU\space Loss=-lnIoU
IoU Loss=1−IoU或IoU Loss=−lnIoU
缺点
失效情况我们首先来看图

如果真实框与预测框没有重合区域,就会出现这样的情况
这种情况并不是少数,因为在模型训练初期,模型的参数趋近于混乱,所以基本上预测框和乱标的没什么太大差别,如果真实框与预测框没有相重合,拟合会较为困难,因为所有的没有重合的损失值都为1,并且没有指明梯度下降的合理方向。他的问题是只考虑了真实框与预测框的相交情况,并没有考虑框的位置关系
GIoU Loss
公式及示意图
G
I
o
U
L
o
s
s
=
1
−
I
o
U
+
∣
C
−
T
∪
P
∣
∣
C
∣
,其中
T
为真实框,
P
为预测框,
C
为两个框的最小边界
GIoU\space Loss=1-IoU+\frac{|C-T \cup P|}{|C|},其中T为真实框,P为预测框,C为两个框的最小边界
GIoU Loss=1−IoU+∣C∣∣C−T∪P∣,其中T为真实框,P为预测框,C为两个框的最小边界

如果是上述不相交的情况

此时虽然1-IoU仍然为1,但是加入的一项会使得两个不相交的框距离越远损失越大,这样可以通过新加入的这一项继续进行梯度下降,这里的GIoU Loss可以大于1
缺点
当一个框被另一个框框住的时候,被框住的框无论在哪个位置,得出的GIoU Loss的值都是完全相同的,这种情况下又会影响梯度下降的方向


在这种情况下,绿框在蓝框里面,无论绿框如何移动,只要它还在蓝框内部,他的损失值就不变,显然这也是不利于框的拟合的,为了解决这种情况,可以采用DIoU
DIoU
公式及示意图
D
I
o
U
L
o
s
s
=
1
−
I
o
U
+
ρ
2
(
c
T
,
c
P
)
d
2
其中
ρ
2
(
c
T
,
c
P
)
是真实框中心
(
c
T
)
与预测框中心
(
c
P
)
的欧氏距离
d
2
是两框对角线距离的平方
DIoU \space Loss=1-IoU+\frac{\rho^2(cT,cP)}{d^2} \\其中\rho^2(cT,cP)是真实框中心(cT)与预测框中心(cP)的欧氏距离 \\ d^2是两框对角线距离的平方
DIoU Loss=1−IoU+d2ρ2(cT,cP)其中ρ2(cT,cP)是真实框中心(cT)与预测框中心(cP)的欧氏距离d2是两框对角线距离的平方

使用DIoU时,不仅可以解决框不相交的问题,又解决了框在内部情况下遇到的问题,此时我们考虑了框的重合度和中心点的距离,还只剩下高宽比这种评价指标。如果深入理解DIoU可以发现在DIoU中,通过IoU和中心距离比的协调,高宽比实际上已经隐含在里边了,不过为了更加容易收敛,仍然可以在多考虑高宽比这一条件并加到损失函数中去
CIoU
这个损失函数画图并不是很好表示,所以只对公式进行讲解,如果理解不了也可以使用DIoU,DIoU也已经达到了很好的效果了
C
I
o
U
L
o
s
s
=
1
−
I
o
U
+
ρ
2
(
c
T
,
c
P
)
d
2
+
α
v
其中
ρ
2
(
c
T
,
c
P
)
是真实框中心
(
c
T
)
与预测框中心
(
c
P
)
的欧氏距离
d
2
是两框对角线距离的平方
CIoU \space Loss=1-IoU+\frac{\rho^2(cT,cP)}{d^2}+ \alpha v \\其中\rho^2(cT,cP)是真实框中心(cT)与预测框中心(cP)的欧氏距离 \\ d^2是两框对角线距离的平方
CIoU Loss=1−IoU+d2ρ2(cT,cP)+αv其中ρ2(cT,cP)是真实框中心(cT)与预测框中心(cP)的欧氏距离d2是两框对角线距离的平方
v
=
4
π
2
(
a
r
c
t
a
n
w
T
h
T
−
a
r
c
t
a
n
w
P
h
P
)
2
v=\frac{4}{\pi ^2}(arctan\frac{wT}{hT}-arctan\frac{wP}{hP})^2
v=π24(arctanhTwT−arctanhPwP)2
α
=
v
1
−
I
o
U
+
v
\alpha=\frac{v}{1-IoU}+v
α=1−IoUv+v
其中
w
T
,
h
T
是真实框的高宽,
w
P
,
h
P
是预测框的高宽
其中wT,hT是真实框的高宽,wP,hP是预测框的高宽
其中wT,hT是真实框的高宽,wP,hP是预测框的高宽







 文章介绍了IoU在目标检测中的重要性,以及针对其不足提出的改进方法,包括GIoU、DIoU和CIoU损失函数。这些改进旨在更好地衡量预测框与真实框的匹配程度,尤其是在处理无重叠和框包含情况时。DIoU考虑了中心距离,而CIoU进一步加入了高宽比的考量,以优化损失函数的性能。
文章介绍了IoU在目标检测中的重要性,以及针对其不足提出的改进方法,包括GIoU、DIoU和CIoU损失函数。这些改进旨在更好地衡量预测框与真实框的匹配程度,尤其是在处理无重叠和框包含情况时。DIoU考虑了中心距离,而CIoU进一步加入了高宽比的考量,以优化损失函数的性能。


















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










