搞定常用的排序方法(C++实现)

排序就是把一个杂乱无章的序列按照从小到大或者从大到小的顺序依次排列，排序的方法有很多，比如最令人感到熟悉的冒泡排序，还有容易理解的插入排序、具有划时代意义的希尔排序，本文将介绍几种常用的排序方法。

首先是冒泡排序，这个排序方式有点像生活中烧开水的时候，那个泡泡从底往上冒，泡泡从小到大的变化。看图：

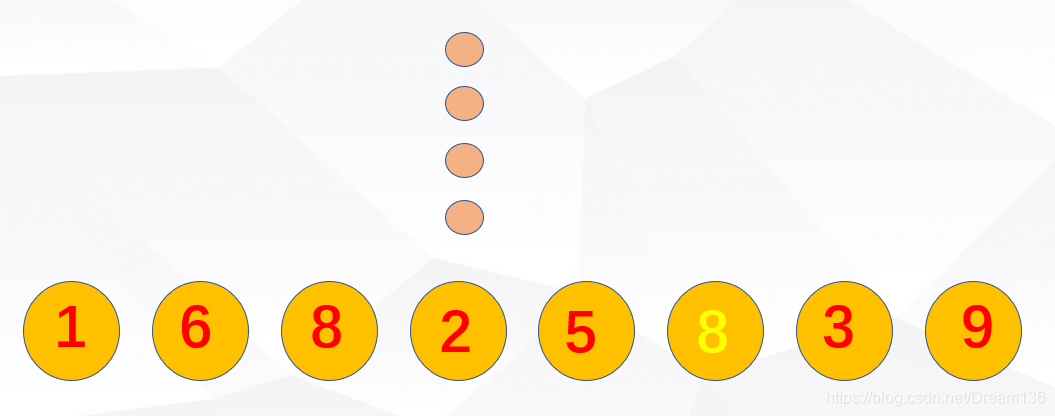
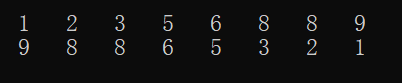
经过一轮循环后，9的位置就确定下来了，就在最后的位置上，确实是的，因为9是这个序列中最大的元素。

开始第二轮循环，这要注意点哦！

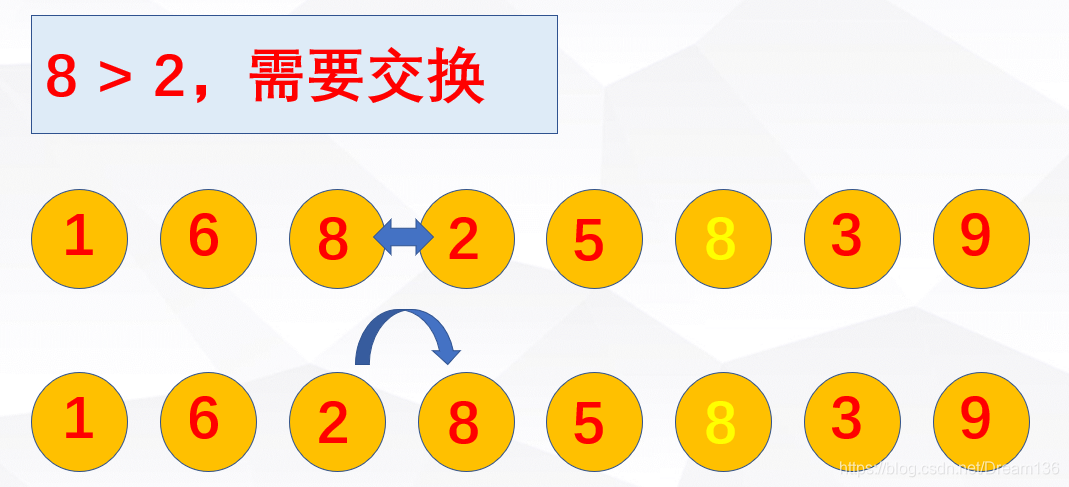
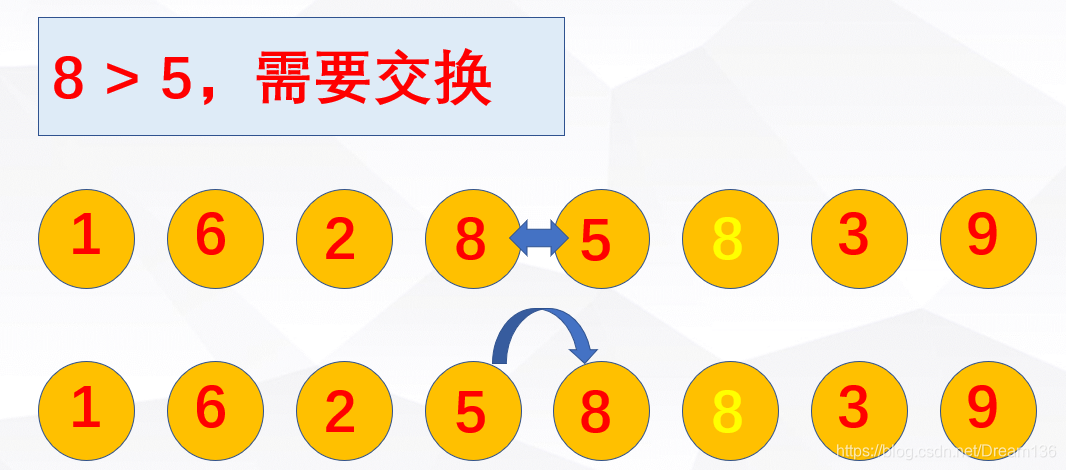
注意啦，注意啦！！！

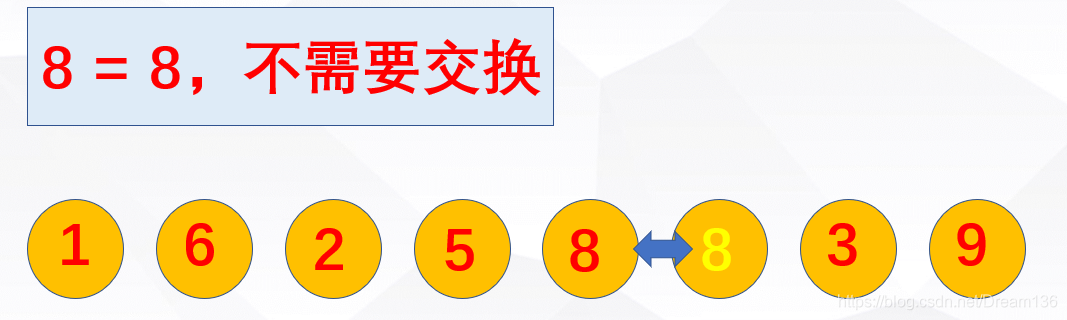
如果相同的元素在排序之后相对位置并没有发生变化，则该排序算法是稳定的。

相信看了这两轮循环的你，已经掌握冒泡排序的本质了，没错，就是对相邻的两个元素进行比较，大的放后面，小的放前面。先来实现第一个版本，也是最简版本。

#include <iostream>

template <typename T>
void bubble(T array[], int len, bool min2max = true) 	// 默认从小到大排序
{
	for(int i = 0; i < len - 1; ++ i)		// 如果有10 个元素，只需要比较 9 趟
	{
		for(int j = 0; j < len - i - 1; ++ j)	// 后面的 i  个元素已经排好序
		{
			if( array[j] > array[j+1] )	// 从小到大排序
			{
				T tem(array[j]);	// 进行交换
				array[j] = array[j+1];
				array[j+1] = array[j];
			}
		}
	}
}

#include <iostream>

using namespace std;

template <typename T>
void bubble(T array[], int len, bool min2max = true)
{
	bool exchange = true;	// 如果在某一次循环里面，没有发生过一次交换
				// 说明整个序列是有序的
	for(int i = 0; i < len - 1; ++ i)
	{
		exchange = false;
		
		for(int j = 0; j < len - i - 1; ++ j)
		{
			if( min2max ? (array[j] > array[j+1] ) : (array[j] < array[j+1]) )	// 使用三目运算符来选择比较的条件
			{
				T tem(array[j]);
				array[j] = array[j+1];
				array[j+1] = tem;
				exchange = true;
			}
		}
	}

}

#include <iostream>

using namespace std;

int main(int argc, const char* argv[])
{
	int a[] = {1,9,6,8,2,5,8,3};

	bubble(a, sizeof(a)/sizeof(*a), true);	// 从小到大排序
	
	for(int i = 0; i < 8; ++ i)
	{
		cout << "  " << a[i] << " ";
	}
	
	bubble(a,sizeof(a)/sizeof(*a), false);	// 从大到小排序
	
	for(int i = 0; i < 8; ++ i)
	{
		cout << "  " << a[i] << " ";
	}
	
	return 0;
}

冒泡排序看懂了，后面的排序算法就会容易理解了。

第二种排序算法，选择排序。选择排序的核心思想是找相对最小元素的下标，然后再将该下标对应的元素与最开始选择的元素进行交换。

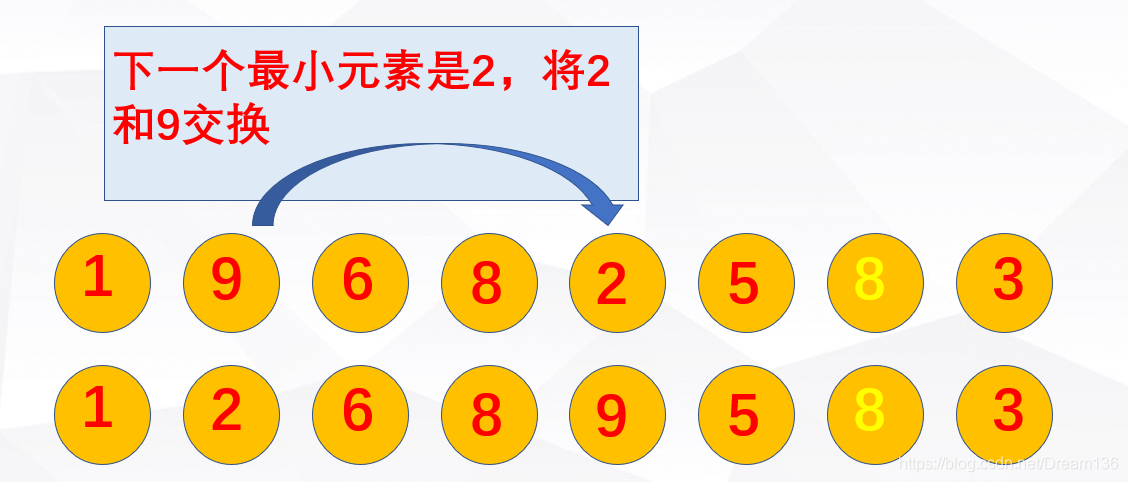
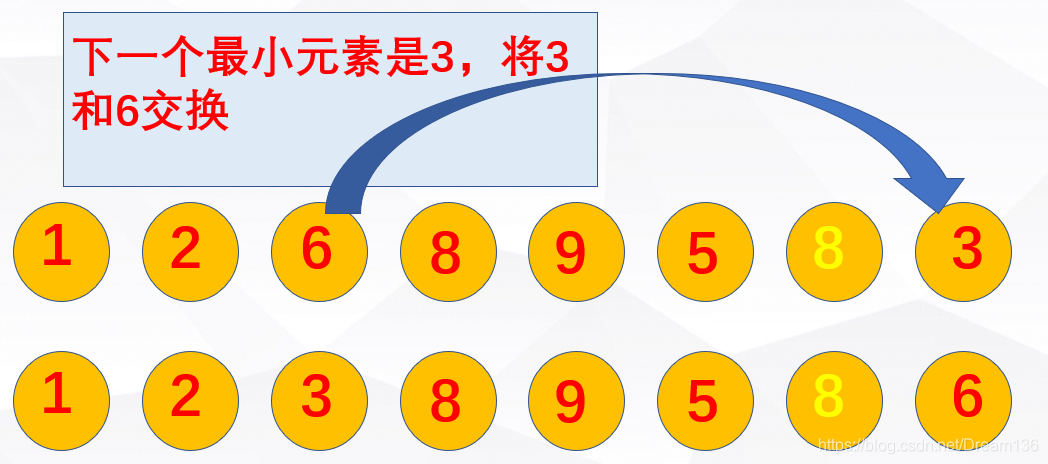
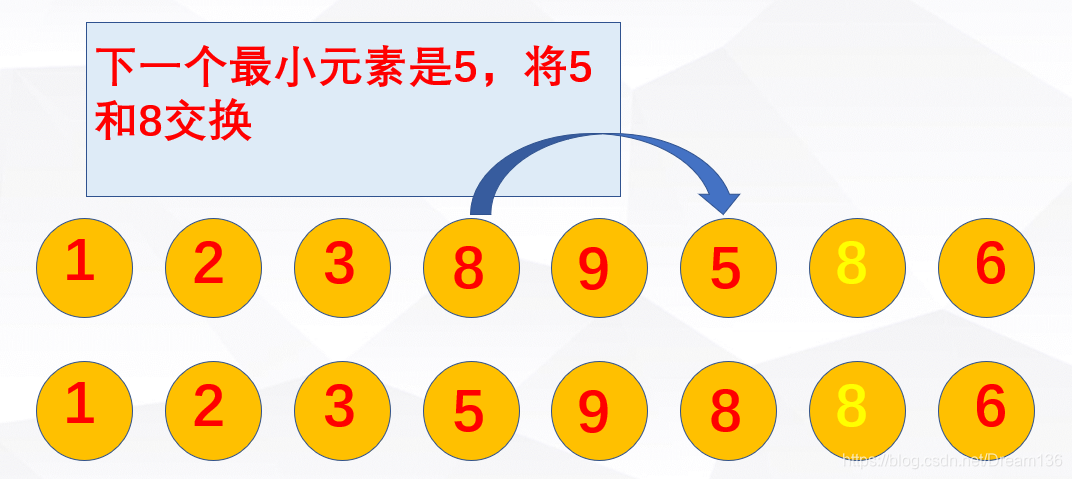
依次寻找每一轮中的最小元素，就可以把整个序列排好。相当简单！！但是选择排序是不稳定的排序算法，因为选择排序交换是跨元素的，所以有可能导致相同元素的相对位置发生改变。

#include <iostream>

template <typename T>
void select(T array[], int len, bool min2max = true)
{
	for(int i = 0; i < len; ++ i)
	{
		int k = i;
		
		for(int j = i + 1; j < len; ++ j)
		{
			if( min2max ? (array[k] > array[j]) : (array[k] < array[j]) )
			{
				k = j;	// 找这一轮循环中的最小元素
			}
		}
		
		if( k!= i )		// 如果是循环开始的元素，就没有必要交换了
		{
			T tem(array[k]);
			array[k] = array[i];
			array[i] = tem;
		}
	}
}

然后就是插入排序，插入排序也是很好理解的。

A picture is worth thousand words. 看图说话！

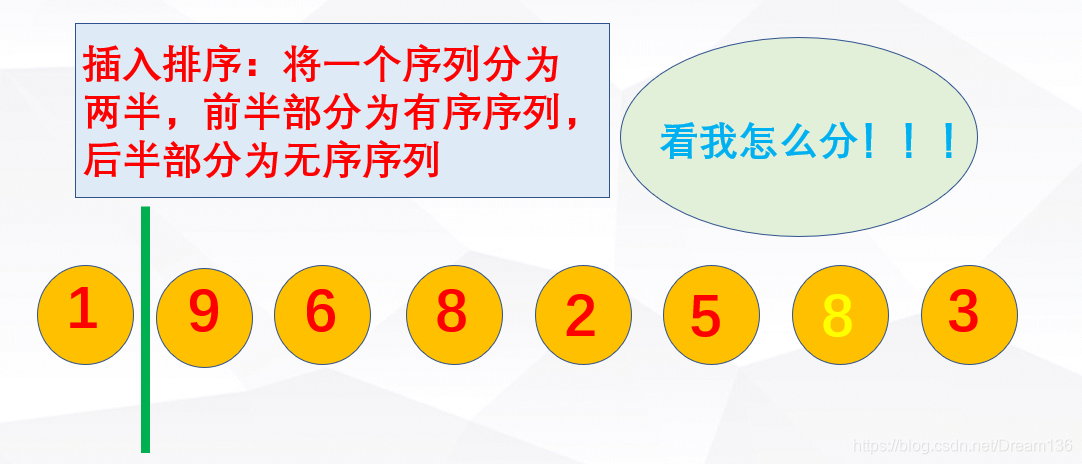
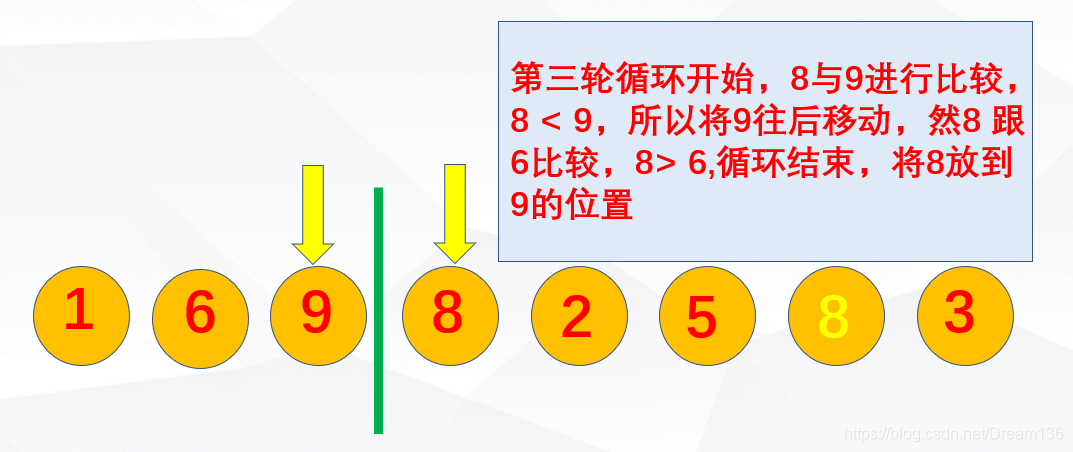
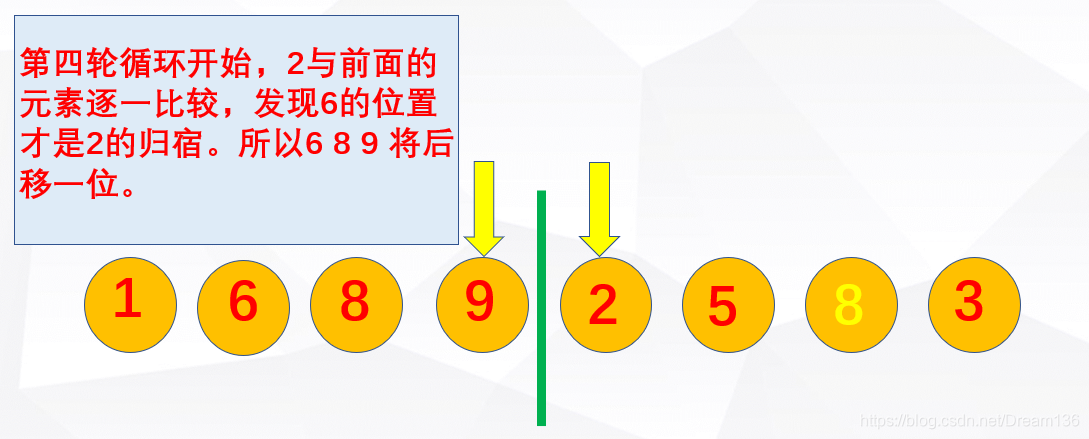
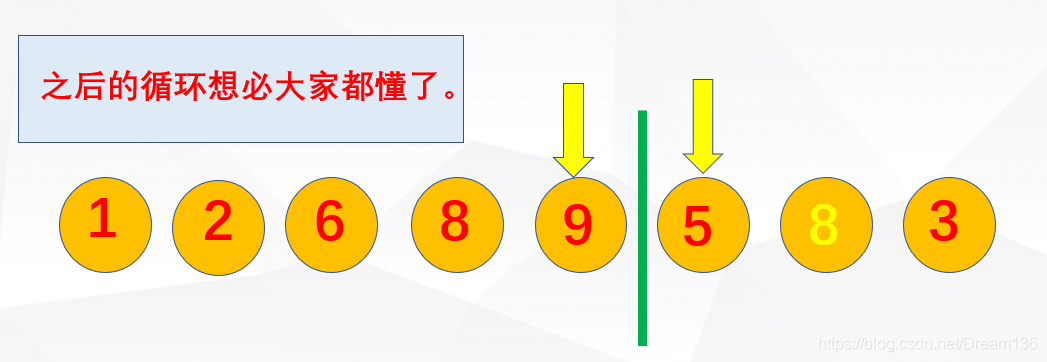
代码实现的时候注意啊！！！上面的图已经提醒我们一旦前面没有要移动的元素，就马上结束循环，反映到代码中：

#include <iostream>

template <typename T>
void insert(T array[], int len, bool min2max = true)
{
	for(int i = 1; i < len; ++ i)
	{
		int k = i;
		T value = array[i];	// 保存当前拿出来比较的元素
		
		for(int j = i - 1; (j >= 0) && (min2max ? (array[j] > value) : (array[j] < value) ); -- j)
		{
			array[j+1] = array[j];	// 如果满足条件，那就往后移动
			k = j;			// 并记录空出来的位置的下标
		}
		
		if( k != i )
		{
			array[k] = value;	// 把元素放到空出来的位置
		}
	}
}

接下来是希尔排序，希尔排序具有划时代的意义并不是因为这种排序算法的效率有多高，而是他打破了长期以来排序算法的时间复杂度不会低于 O(n2) 的魔咒，在这之后，涌现出越来越多高效的排序算法！

#include <iostream>

template <typename T>
void shell(T array[], int len, bool min2max = true)
{
	int s = len;	
	
	do
	{
		d = d/3 + 1;	// 取间隔，这样做效率会高一点
		
		for(int i = d; i < len; i += d)	// 以d 为间隔做插入排序
		{
			int k = i;
			T value = array[i];
			
			for(int j = i - d; (j >= 0) && (min2max ? (array[j] > value) : (array[j] < value) ); j -= d)
			{
				array[j+d] = array[j];
				k = j;
			}
			
			if( k != j )
			{
				array[k] = value;
			}
		}
	}
	while( d > 1 );
}

轮到递归的排序算法了！先是归并排序算法出场。归并排序的思想是先将一个无序序列不断地划分为仅有一个元素的序列，那么这个序列就是有序序列（仅有一个元素的序列一定有序），然后将该有序序列与另一个有序序列进行合并，需要额外的辅助内存空间。具体可以看图！

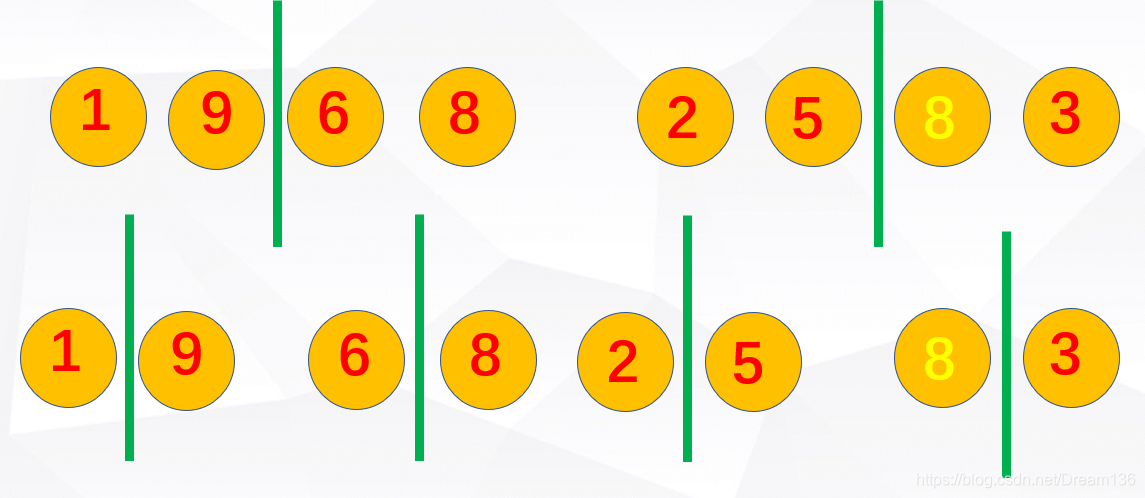
分完了，总得合起来是吧。

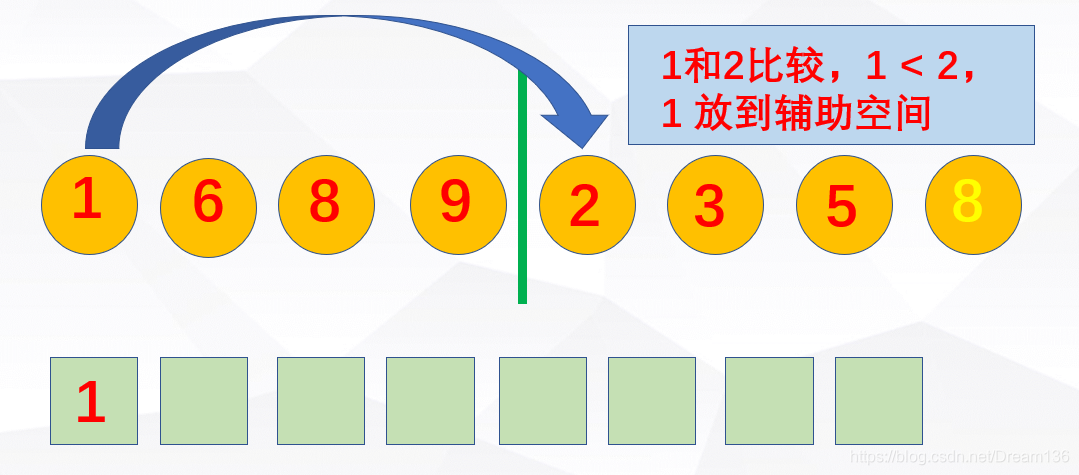
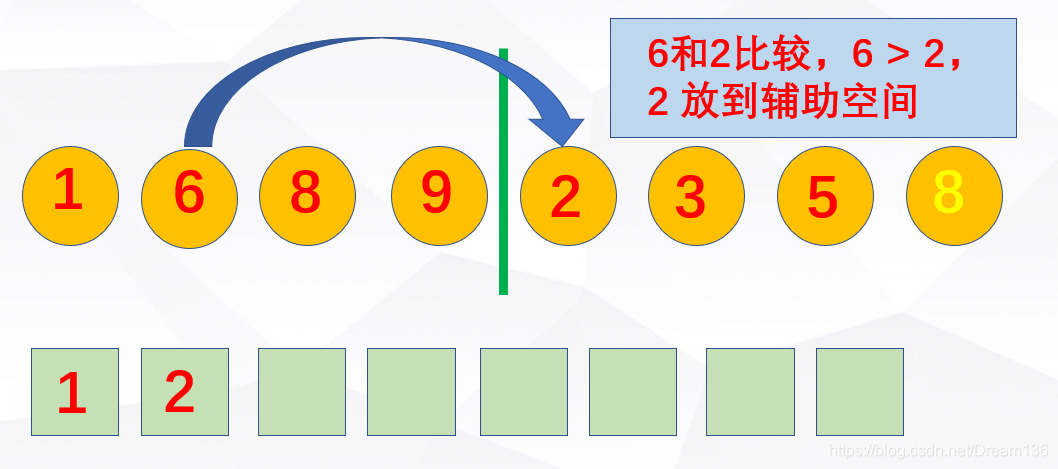
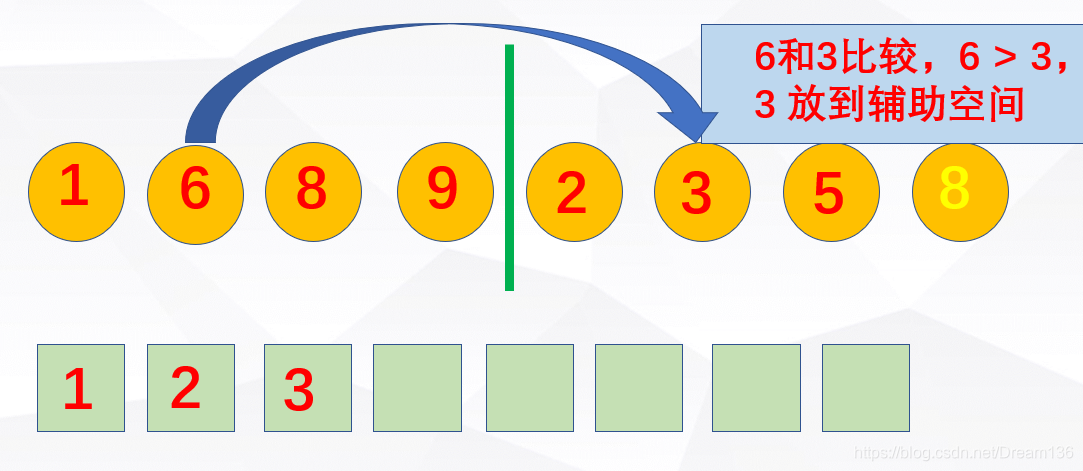
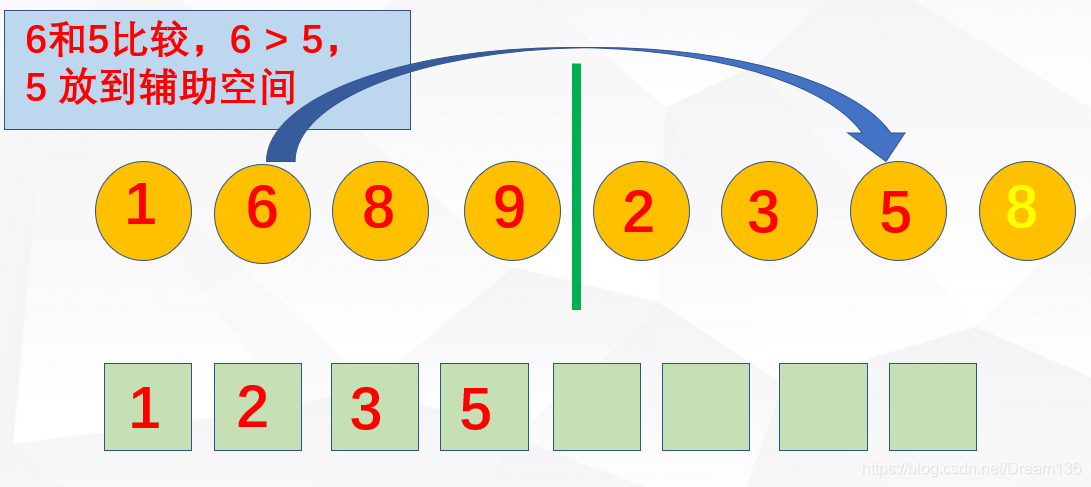
继续下去总会排好的。

但要注意的是，不要跳进递归的圈套里，毕竟我们不是计算机！！！

#include <iostream>

template <typename T>	// 做合并的函数
void merge(T array[], T space[], int begin, int mid, int end, bool min2max)
{
	int i = begin;		// 第一个序列的起点
	int j = mid + 1;	// 第二个序列的起点
	int k = begin;		// 辅助空间的起点
	
	while( (i <= mid) && (j <= end) )	// 开始合并
	{
		if( min2max ? (array[i] < array[j]) : (array[i] > array[j]) )
		{
			space[k++] = array[i++];
		}
		else
		{
			space[k++] = array[j++];
		}
	}

	while( i <= mid )	// 如果两序列不是一样长，就会有一部分剩余，直接放到辅助空间就行了
	{
		space[k++] = array[i++];
	}
	
	while( j <= end )	// 同理
	{
		space[k++] = array[j++];
	}
	
	for(int i = begin; i <= end; ++ i)	// 将数据从辅助空间放回原数组
	{
		array[i] = space[i];
	}
}

template <typename T>	// 真正的递归函数，将序列拆分
void merge(T array[], T space[], int begin, int end, bool min2max)
{	
	if( begin < end )
	{
		int mid = (begin + end) / 2;			// 求中间值
		merge(array, space, begin, mid, min2max);	// 对前半部分继续分
		merge(array, space, mid + 1, end, min2max);	// 对后半部分继续分
		merge(array, space, begin, mid, end, min2max);	// 调用第一个合并函数
		
	}
}

template <typename T>	// 提供给用户使用的真正的归并排序函数
void merge(T array[], int len, bool min2max = true)
{
	T* space = new T[len];		// 申请一段辅助空间
	
	merge(array, space, 0, len - 1, min2max);

	delete[] space;			// 用完需要归还
}

介绍最后一个排序算法啦，也是我经常使用的排序算法----快速排序！

快速排序的核心思想是找中位值，将中位值作为基准，将无序序列分为两半。然后再分别从前半部分和后半部分找中位值，这种做法是什么？

很明显是递归嘛！看图说话：

#include <iostream>

template <typename T>		// 找中位值
int middleValue(T array[], int begin, int end, bool min2max)
{
	T value = array[begin];	// 假设第一个元素是中位值
	
	while( begin < end )
	{
		while( (begin < end) && (min2max ? (array[end] > value) : (array[end] < value) ) )
		{
			-- end;		// 从序列的末尾元素开始与中位值进行比较
		}
		
		T tem1(array[end]);	// 与中位值进行交换
		array[end] = array[begin];
		array[begin] = tem1;
		
		while( (begin < end) && (min2max ? (array[begin] < value) : (array[begin] > value) ) )
		{
			++ begin;	// 从序列的首元素开始与中位值进行比较
		}
		
		T tem2(array[begin]);	// 与中位值进行交换
		array[begin] = array[end];
		array[end] = tem2;
	}
	
	return begin;
}

template <typename T>
void quick(T array[], int begin, int end, bool min2max)
{
	if( begin < end )
	{
		int pivot = middleValue(array, begin, end, min2max);
		
		quick(array, begin, pivot - 1, min2max);	// 对前半部分递归找中位值
		quick(array, pivot + 1, end, min2max);		// 对后半部分找中位值
	}
}

template <typename T>		// 提供给用户使用的函数
void quick(T array[], int len, bool min2max = true)
{
	quick(array, 0, len - 1, min2max);
}

排序算法还是挺重要的，需要好好学习！