归并排序的概述
- 将n个记录看成是n个长度为1的有序子表;
- 将两两相邻的有序子表进行归并,若子 表数为奇数,则留下的一个子表直接进入下一 次归并;
- 重复步骤(2),直到归并成一个长度为n 的有序表
归并排序
重要参数
- a【】:存储来的数据
- b【】:归并排序的辅助数组
- min:输入排序序列的起始位置
- max:输入排序序列的终点位置
- mid:将要排序序列的中间值
- p:从mid位置开始向后扫的一个指针
- min:记录一开始min的值,为之后辅助数组b【】导入回a【】铺垫
算法思想
- 首先判断一下当前将要排序的序列是否为一个单位(即长度为一),若是,则返回。(为后续的递归铺垫)
- 通过输入的min和max求出其中间值mid,并将p指向mid;
- 以mid为中枢,首先向mid左边进行递归排序,即min~mid;
- 以mid为中枢,向mid右边进行递归排序,即mid~max;
- 开始归并排序,以mid为中界限,一个指针从min开始,一个指针从mid开始,比较大小,较小的排在前面,每次排序完后判断一下min指针是否到了mid的位置或是p指针到了max的位置;
- 若是到了,则将未排序完的序列进行补充到已排序的后面,则排序结束。
- 将辅助数组中的数据导入回原本的数组
改进后的想法
上面的想法及代码是第一次写归并排序的时候写的,有很多地方很拙劣
- 1.首先是利用一个for循环和两个if语句进行归并,使得代码表达的意思不清晰
- 2.两个if语句的比较显得有些多余,因为这就是不是大于就是小于等于的情况
- 3.累赘,每个if语句后又来了一次 if 来判断两个子序列之一是否扫描完
改进的想法(无代码)
- 使用一个while循环来替代for循环和判断两个子序列是否扫描完,while(两个训练均为扫描完时为真)
- 在第一个while循环完再添加两个独立的while循环,来判断是哪个子序列先排序完。
算法分析
- 时间复杂度:O(NlogN)
- 辅助空间:O(N)
源代码
#include <stdio.h>
#include <stdlib.h>
#define MAX 10000
void merge(int a[],int b[],int min,int max)//归并排序,a[]数组为原始数组,b[]数组为辅助的数组
{
int mid,p;//mid为数组的中间位置,p为从中间位置开始的指针
int min2;//记录了数组最小的位置
int i,j;
min2=min;//min为从最小位置开始的指针
if((max-min)<=1)//如果数组为1则return
{
return;
}
mid=(max+min)/2;//计算中间位置
p=mid;
merge(a,b,min,mid);//向中间位置的左边递归
merge(a,b,mid,max);//向中间位置的右边递归
for(i=min;i<max;)//开始归并排序
{
if(a[min]>a[p])//左边大于右边
{
b[i]=a[p];
p++;
if(p==max)//判断是否排序完成
{
i++;
for(j=min;j<mid;j++,i++)
{
b[i]=a[j];
}
}
else
{
i++;
}
}
if(a[min]<=a[p])//右边大于左边
{
b[i]=a[min];
min++;
if(min==mid)//判断是否排序完成
{
i++;
for(j=p;j<max;j++,i++)
{
b[i]=a[j];
}
}
else
{
i++;
}
}
}
for(i=min2;i<max;i++)//整理排序后的数组
{
a[i]=b[i];
}
}
int main()
{
int a[MAX],b[MAX];//a【】数组用于存储原始的数组,b【】数组用于归并排序中的辅助数组
int length;
int i;
printf("请输入要排序的个数:\n");
scanf("%d",&length);
getchar();
printf("请输入数据:\n");
for(i=0;i<length;i++)
{
scanf("%d",&a[i]);
getchar();
}
merge(a,b,0,length);
printf("排序后:\n");
for(i=0;i<length;i++)
{
printf("%d ",a[i]);
}
}
测试样例
25
5 8 9 6 7 4 3 5 2 1 11 18 19 17 21 26 29 35 38 31 36 30 34 32 70
测试结果
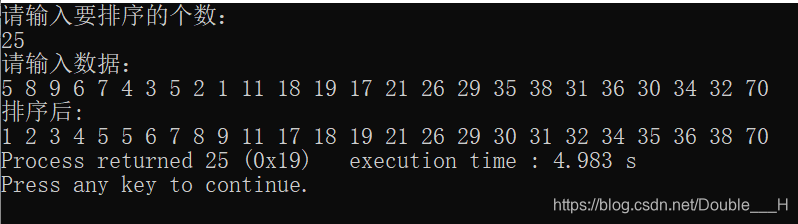







 本文介绍了归并排序的原理,包括将数据分为多个长度为1的子表,然后逐步归并成一个有序表的过程。详细阐述了算法思想,包括递归排序、归并操作以及如何优化代码,减少了多余的比较和判断。最后,分析了归并排序的时间复杂度为O(NlogN)和辅助空间需求为O(N),并给出了源代码及测试样例。
本文介绍了归并排序的原理,包括将数据分为多个长度为1的子表,然后逐步归并成一个有序表的过程。详细阐述了算法思想,包括递归排序、归并操作以及如何优化代码,减少了多余的比较和判断。最后,分析了归并排序的时间复杂度为O(NlogN)和辅助空间需求为O(N),并给出了源代码及测试样例。
















 1259
1259

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








