leetcode704 二分查找（C++ & python3）

本文参考卡哥的代码随想录，加上了一点自己的理解，感谢Carl的分享。

一. 题目

力扣704题

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例一

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例二

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

• 你可以假设 nums 中的所有元素是不重复的。
• n 将在 [1, 10000]之间。
• nums 的每个元素都将在 [-9999, 9999]之间。

目标：熟悉根据 “左闭右闭” “左闭右开” 两种区间规则写出二分法。

二. 题目分析

1. 解题方法

有序数组+数组中无重复元素（如果有重复元素那么二分法查找返回的元素下表不是唯一的）则组使用二分法查找

2. 使用要点

二分法逻辑简单但很多边界条件需要注意，例如
while(left < right)orwhile(left <= right)？
right = middleorright = middle - 1?

3. 突破口

想清楚区间的定义（也就是不变量）。每一次区间的处理要根据区间的定义来操作（“循环不变量”规则）。
二分法的区间定义一般为两种，左闭右闭[left, right] 和 左闭右开[left, right)，对应着right = middle与right = middle - 1

三. 二分法的两种实现方法 C++ 版

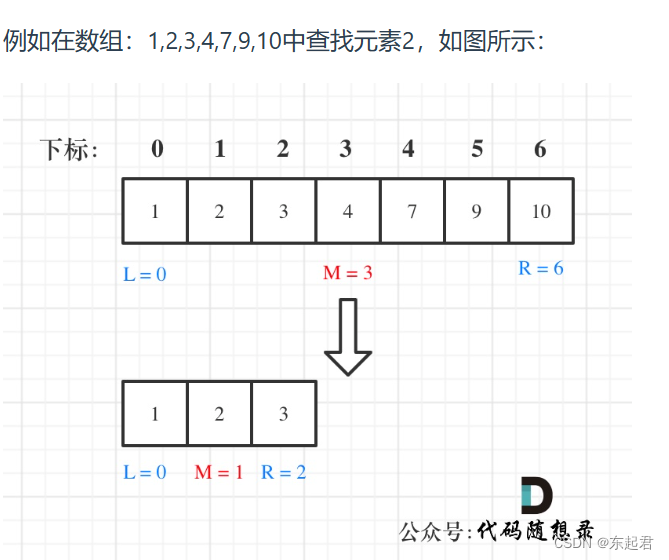
1. 左闭右闭

定义target在[left, right]里，则有以下两点:

• while (left ? right)：因为left == right 是有意义的，所以使用 “<=”。（先考虑定义区间是否有意义，剩下的代码逻辑不用管）
• 条件语句if (nums[middle] > target)里对right的赋值：因为此时的nums[middle]不是target，并且判断区间是闭区间，所以接下来查找的左区间的结束位置是middle - 1。
  
  代码：

//左闭右闭（C++）
class Solution {
public:
	int search(vector<int>& nums, int target){
		int left = 0;
		int right = nums.size() - 1; //定义target在[left, right]内
		while (left <= right) { // 当left==right，区间[left, right]依然有效，所以用 <=
			int middle = left + ((right - left) / 2);
			if (nums[middle] > target) {
				right = middle - 1; // target在左区间，所以[left, middle - 1]
			} else if (nums[middle] < target){
			left = middle + 1; // target在右区间，所以[middle + 1, right]
			} else{ // nums[middle] == target
				return middle;
			}
		}
		return -1; //未找到目标
	}
};

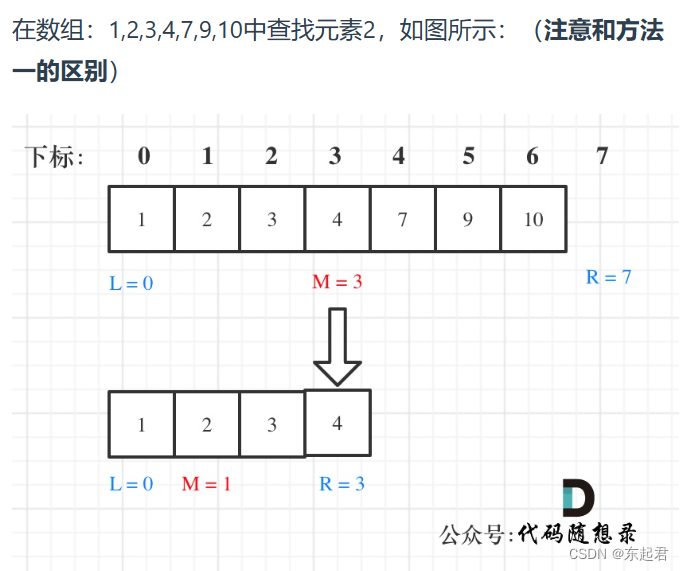
2. 左闭右开

定义target在[left, right)里，则有以下两点:

• while (left ? right)：因为left == right 是没有意义的，所以使用 “<”
• 条件语句if (nums[middle] > target)里对right的赋值：因为此时的nums[middle]不是target，在左区间继续寻找，并且判断区间是右开区间，不会比较nums[middle]，所以right更新为middle。
  
  代码：

//左闭右开(C++)
class Solution {
public:
	int search(vector<int>& nums, int target){
		int left = 0;
		int right = nums.size(); // target定义左闭右开区间
		while (left < right){ // 因为target的定义区间所以left = right 无意义
			int middle = left + ((right - left)>>1); // ">>1"相当于"/2"
			if (nums[middle] > target) {
			right = middle; // target 在左区间，在[left, middle)中
			} else if(nums[middle] < target){
				left = middle + 1; // target 在右区间，在[middle + 1, right)中
			} else {
				return middle;
			}
		}
		return -1;
	}
};

四. 二分法的两种实现方法 python3 版

代码：

#左闭右闭
class Solution:
	def search(self, nums: List[int], target: int) -> int:
		left, right = 0, len(nums) - 1
		while left <= right:
			middle = left + (right - left)//2
			if nums[middle] > target:
				right = middle - 1
			elif nums[middle] < target:
				left = middle + 1
			else:
				return middle
		return -1

#左闭右开
class Solution:
	def search(self, nums: List[int], target: int) -> int:
		left, right = 0, len(nums)
		while left < right:
			middle = left + (right - left) // 2
			if nums[middle] > target:
				right = middle
			elif nums[middle] < target:
				left = middle + 1
			else:
				return middle
		return -1

五. 小知识点

1. 运算符优先级

（C++）int middle = left + ((right - left)>>1);与int middle = left + (right - left)>>1;的结果不同，后者会超出时间限制。
== 运算符"+“, “-” 的优先级大于”<< “, " >>” ==

详细表（参考链接）

优先级	运算符	结合律	助记
1	::	从左到右	作用域
2	a++、a– type()、type{} a()、a[] . 、->	从左到右	后缀自增减、 函数风格转型、 函数调用、下标、 成员访问
3	!、~、 ++a、–a、+a、-a、 (type)、sizeof、&a、 *a、new、new[]、delete、 delete[]	从右到左	逻辑非、按位非、 前缀自增减、正负、 C风格转型 、取大小、取址、 指针访问、 动态内存分配
4	.*、 ->*	从左到右	指向成员指针
5	a*b、a/b、a%b	从左到右	乘除、取模
6	a+b、a-b	从左到右	加减
7	<<、>>	从左到右	按位左右移
8	<、<=、>、>=	从左到右	比较大小
9	a&b	从左到右	按位与
10	^	从左到右	按位异或
11	&&	从左到右	逻辑与

2. middle的两种算法

middle = (left + right) / 2; 或 middle = left + ((right - left) / 2);

3. 乘除运算与移位运算的关系

“左移乘，右移除”
eg: u<<3 == u*8;   (u<<5) - (u<<3) == 2⁵ *u - 2³*u== u*24;
  u>>1 == u/2;

4. C++中vector的用法

参考链接