系列文章目录
leetcode - 双指针问题_leetcode双指针题目-优快云博客
leetcode - 滑动窗口问题集_leetcode 滑动窗口-优快云博客
目录
2、给一个数 n ,确定它的二进制表示中第 x 位是 0 还是 1
前言
路漫漫其修远兮,吾将上下而求索;
大家可以先自己尝试做一下喔~
- 191. 位1的个数 - 力扣(LeetCode)
- 338. 比特位计数 - 力扣(LeetCode)
- 461. 汉明距离 - 力扣(LeetCode)
- 136. 只出现一次的数字 - 力扣(LeetCode)
- 260. 只出现一次的数字 III - 力扣(LeetCode)
- 面试题 01.01. 判定字符是否唯一 - 力扣(LeetCode)
- 268. 丢失的数字 - 力扣(LeetCode)
- 371. 两整数之和 - 力扣(LeetCode)
- 137. 只出现一次的数字 II - 力扣(LeetCode)
- 面试题 17.19. 消失的两个数字 - 力扣(LeetCode)
一、常见位运算总结
注:我们将最右边的比特位记为第0位
1、基础位运算
- << 左移操作符 :按二进制形式把所有的数字向左移动对应的位数,高位移出(舍弃),低位的空位补零
- >> 右移操作符 :按二进制形式把所有的数字向右移动对应位移位数,低位移出(舍弃),高位的空位补符号位,即正数补零,负数补1。
- ~ 按位取反 :按照二进制位取反 , 即 1 变为0 ,0 变为1
- & 按位与 : 有0 则为0,全1才为1
- | 按位或 :有1 则为1 ,全0 才为0
- ^ 按位异或 :相同为0,相异为1
2、给一个数 n ,确定它的二进制表示中第 x 位是 0 还是 1
思考:将1向左移动x 位,然后与 n 按位与(&),所得结果为0则第 x 位是 0 ,所得结果不为0那么第 x 位是 1;或者让 n 向右移动 x 位,然后与 1 按位与,所得结果为0则第 x 位是 0 所得结果为1那么第 x 位是 1;
(1<<x)&n 或者 (n>>x)&1
还需要注意运算符的优先级,最简单的方法就是能加括号就加括号;
3、将一个数 n 的二进制表示的第 x 位修改为1
思考:将1向左移动 x 位然后与 n 按位或(|)
n = (1<<x)|n , 可以简写为 n|=(1<<x);
4、将一个数n 的二进制表示的第 x 为修改为0
思考:将 1 向左移动 x 位,然后取反,再与 n 按位与(&);
n = (~(1<<x))&n , 可以简写为:n&=(~(1<<x))
5、位图的思想
位图的本质是一个哈希表;哈希表在很多情况下是一个数组(在数组中记录一些值,方便我们增删查改) , 而现在我们可以利用比特位来记录信息,仅需要一个变量的二进制位来记录我们的信息;
Sum: 位图的思想本质上是一个哈希表,此时的哈希表不是用数组来实现的,而是用一个整型变量的比特位来帮助我们记录信息;
6、提取一个数 n 的二进制表示中最右侧的1
首先我们需要了解一个小知识点:如果一个数取负数,那么就是将这个数按位取反然后再+1;
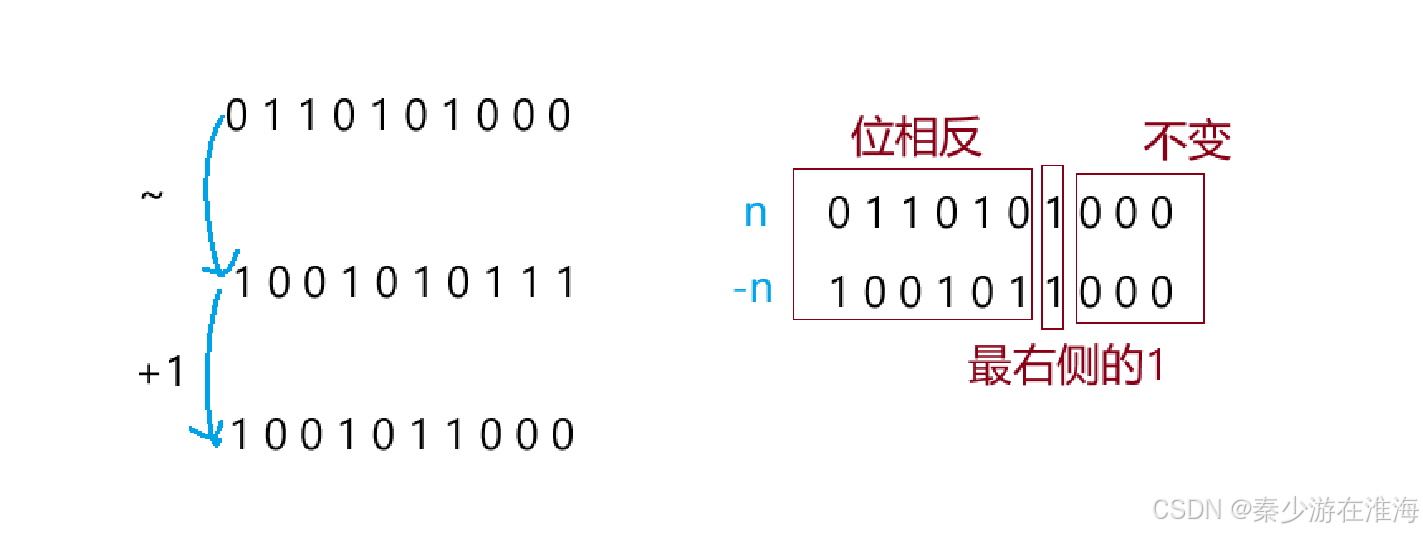
经过(-n) 操作之后,最右侧的1 将这个数的位划分成了两个部分,其左边全部是位相反,而有部分没有改变;那么将 n 与 (-n) 按位与就会消除最右侧1 的左部分位,那么就可以得到最右侧的1;
n&(-n)
7、干掉一个数 n 二进制表示中最右侧的1
首先我们需要了解一个小知识点:(n-1) 的含义
(n-1)的本质是将最右侧的1以及其左部分“按位取反”,而其有部分的位不变:
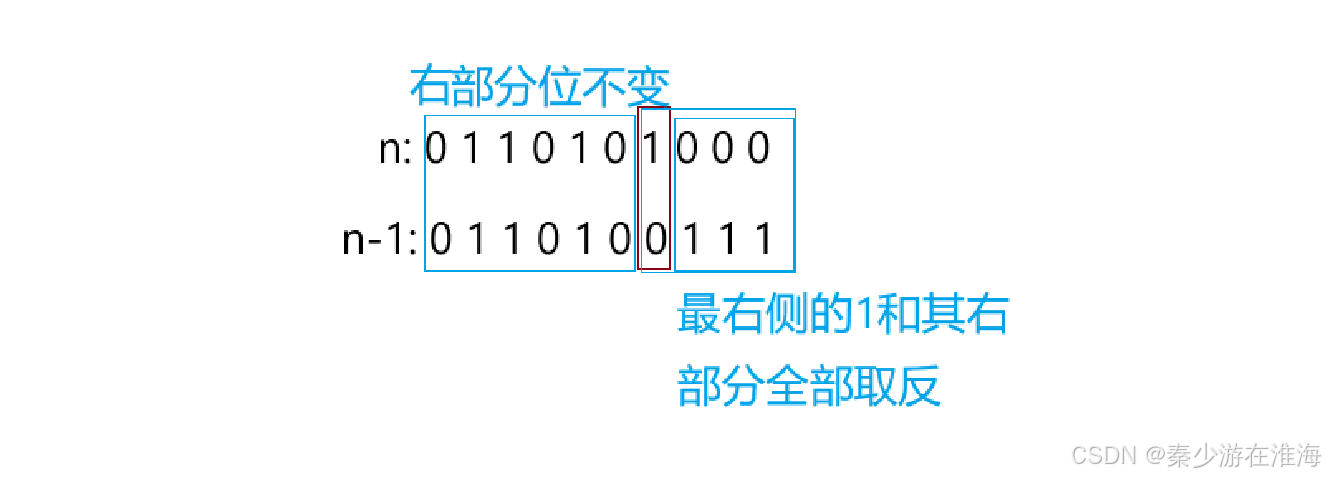
那么 n 与 (n-1) 按位与就可以去除“按位取反”的那部分位,即实现干掉一个数 n 二进制表示中最右侧的1;
n = n&(n-1) , 简写为: n &=(n-1);
8、位运算的优先级
~(按位取反 - 单目运算符,优先级很高)
<<,>>,>>>(移位)
&(按位与)
^(按位异或)
|(按位或)
最佳实践:使用括号!
由于位运算符的优先级规则复杂且容易记错(尤其是与 ==/!= 的关系),强烈建议在复杂的表达式中大量使用括号 ( ) 来明确指定运算顺序。这不仅能避免错误,还能大大提高代码的可读性。
9、按位异运算的运算律

Q:如何证明 a^b^c = (a^b)^c ?
- 我们可以将按位异或简单理解为无进位相加;那么这些数按位异或在一起,本质上就是来抵消1 的;

在抵消这些1 的时候,并不会考虑这些1 的顺序;这三个数按位异或在一起,只要它们对应的二进制位为 1 , 两两之间就可以抵消;因此按位异或的计算是绝对符合交换律以及结合律的;
二、题解
1、题1 位1的个数:
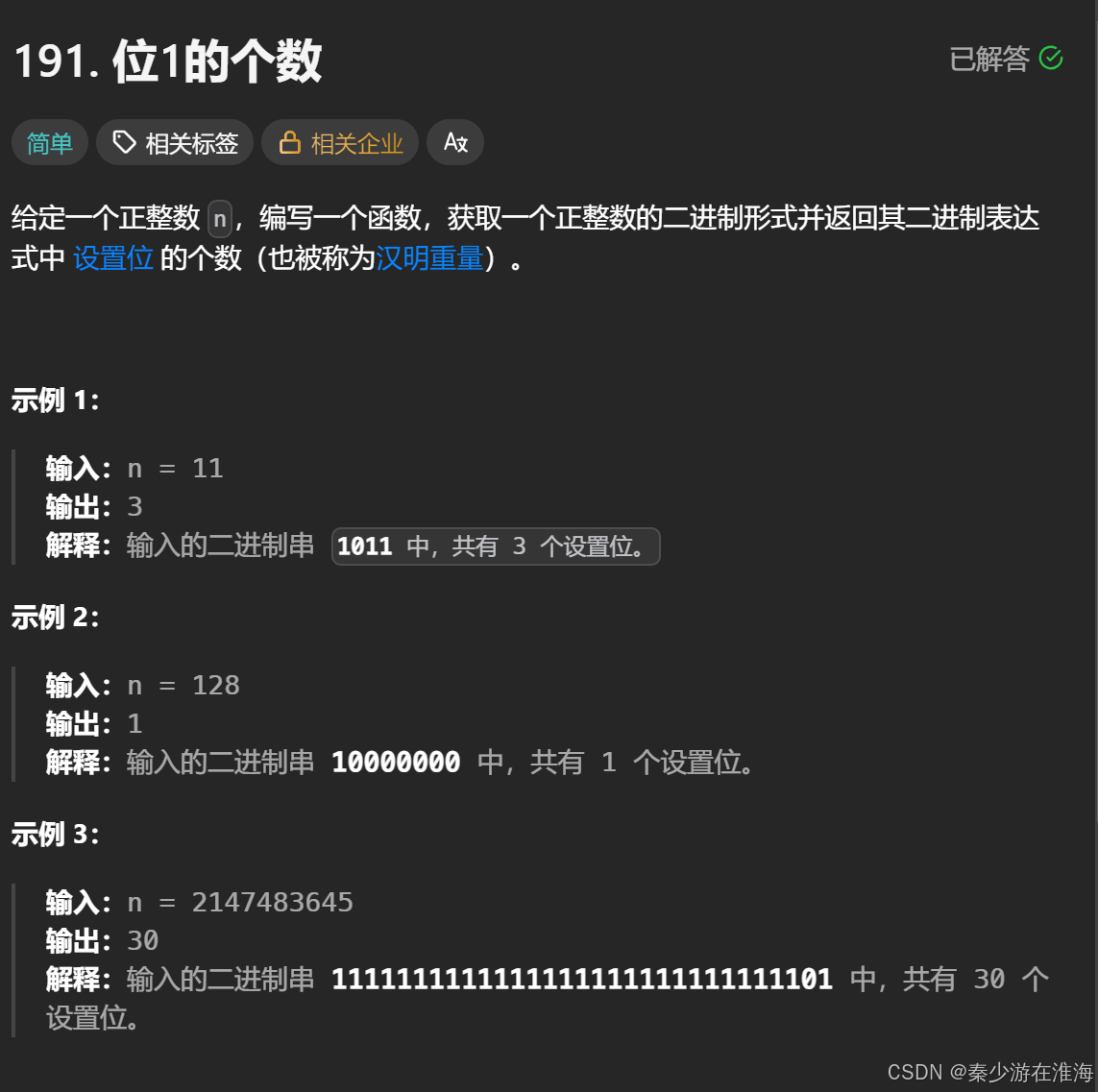
解法一:暴力解法
遍历每一个比特位,然后统计出现了多少个1即可;
参考代码;
int hammingWeight(int n)
{
//暴力
int count = 0 , ret = 0;
while(count!=32)
{
if(1&(n>>count)) ret++;
count++;
}
return ret;
}解法二:去除最右侧的1
统计操作了多少次即可;需要注意的是,去除最右侧的1: n = n&(n-1)
参考代码:
int hammingWeight(int n)
{
//去除最右侧的1,统计操作了多少次
int ret = 0 ;
while(n)
{
n = n&(n-1);
ret++;
}
return ret;
}2、题2 比特位计数:
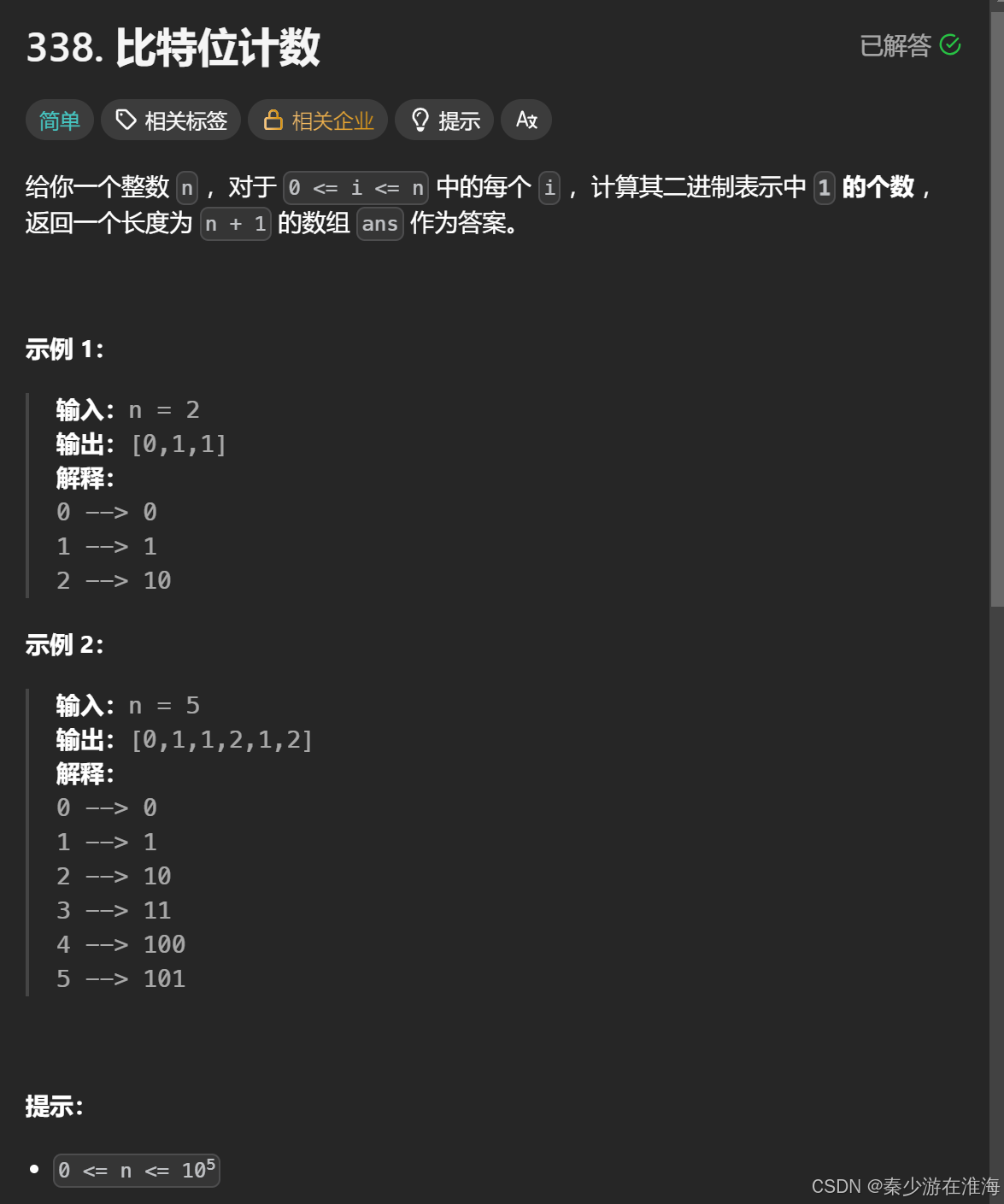
无非就是在外层套一个循环,枚举0~n 的数据,然后依次算出该数中二进制位中1 的个数,将结果放到对应下标的数组中;
此处计算数的二进制位可以采用暴力统计,也可以采用去除最右侧1 然后统计操作次数的方法;此处采用去除最右侧1 然后统计操作次数;
参考代码:
vector<int> countBits(int n)
{
//去除最右侧1 然后统计操作次数
vector<int> ans(n+1);
for(int i = 0 ;i<=n;i++)
{
int j = i , count = 0;
while(j)
{
j = j&(j-1);
count++;
}
ans[i] = count;
}
return ans;
}3、题3 汉明距离 :
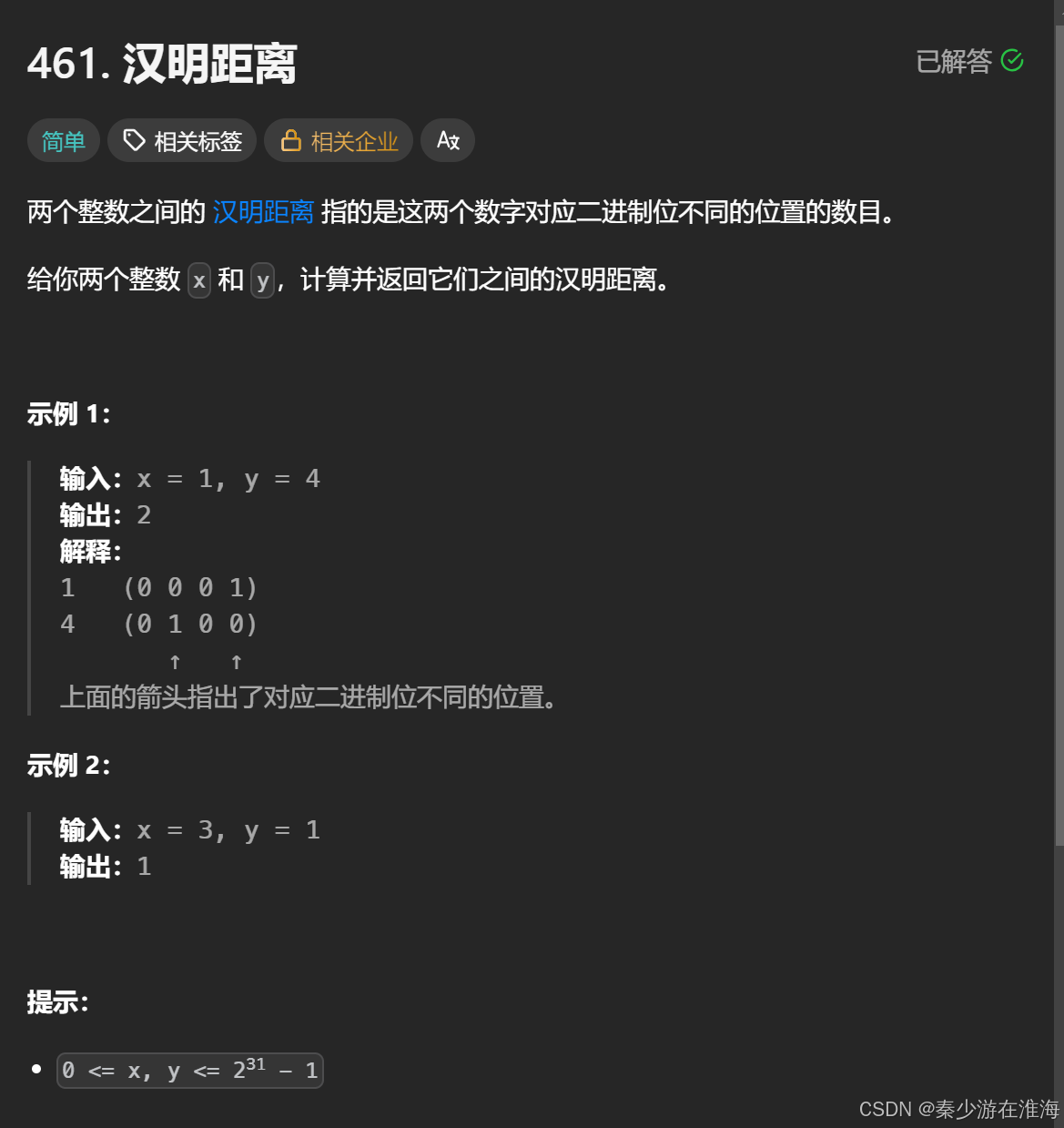
统计不同的位数,难免会想到按位异或(^) : 相同为0,相异为1;那么只需要让这两个数按位异或,然后再统计按位异或结果中位1 的个数即可;而统计二进制位中1的个数,可以暴力遍历,也可以采用去除最右侧1 然后统计操作次数的方法;此处采用去除最右侧1 然后统计操作次数;
参考代码:
int hammingDistance(int x, int y)
{
//按位异或
x = x^y;
//统计 x 中 1 的个数
int ret = 0;
while(x)
{
x = x&(x-1);
ret++;
}
return ret;
}4、题4 只出现一次的数字:

根据按位异或的运算律:

相同的数按位异或结果会得到0,而一个数与0按位异或会得到其本身;
根据这个特性,可以直接将nums 中的数据进行按位异或,最后得到的结果就是只出现一次的数;
参考代码:
int singleNumber(vector<int>& nums)
{
int ret = 0;
for(auto e: nums) ret^=e;
return ret;
}5、题5 只出现一次的数字 III :
260. 只出现一次的数字 III - 力扣(LeetCode)
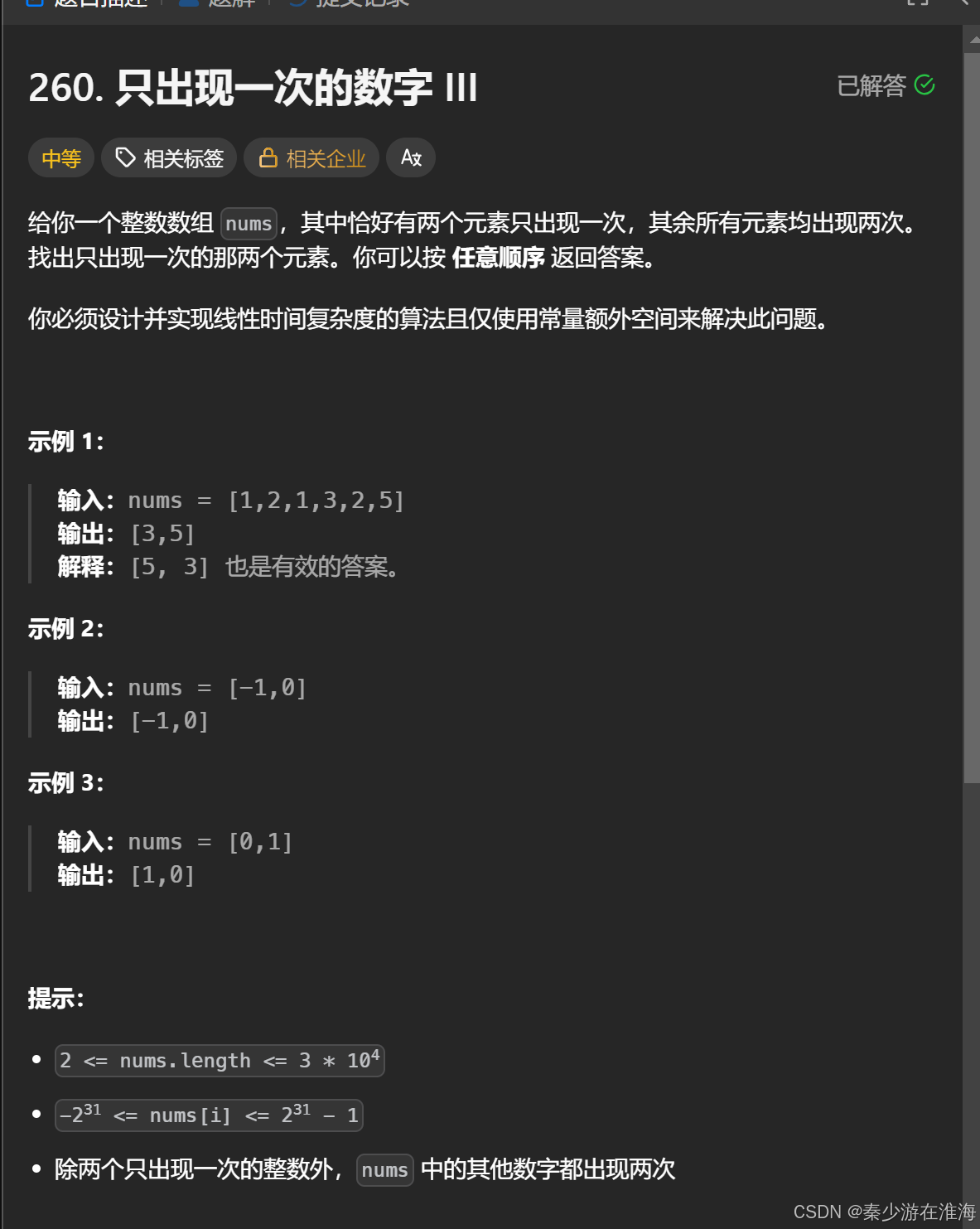
根据上题的思路,当一个数组中全是两两相同的数,只有一个是单独出现的,将其按位异或就可以得到这个数;但是本题中,是两个单独出现的数,那么将nums 中的数据按位异或的结果是这两个单独出现的数按位异或的结果;显然直接将nums 中的数据进行按位异或处理是行不通的;
而一个数是由其所有二进制位相加得到的结果,如果两个数不同,那么其二进制位也一定不相同,那么我们可以利用某一个二进制来区分这两个数,将数组nums 中的数据划分为两部分,在这两部分中分贝按位异或,最后结果就是所求的两个单独出现的数;
Q:如何找到可以区分这两个数的位?
- 将nums 中的数据全部进行按位异或,所得到的结果必定是这两个只出现一次数据按位异或的结果,假设这个结果为x ;而按位异或:相同为0,相异为1;那么x 中的二进制位中的1全都是这两个单独出现的数可以将其区分的位;使用的时候取x 最右边的1就可以了;
而获取最右的1 : x&(-x)
其中还需要注意的是,由于![]() ,所以我们在将nums 中的数据全部都进行按位异或的时候需要使用 long long 类型的变量;
,所以我们在将nums 中的数据全部都进行按位异或的时候需要使用 long long 类型的变量;
参考代码:
vector<int> singleNumber(vector<int>& nums)
{
//根据二进制位的不同,将数组中的数据分为两个部分
long long x = 0;
for(auto e: nums) x^=e;
//获取x 最右的1作为区分的依据
long long flag = x&(-x);
int ret1 = 0 , ret2 = 0;
for(auto e: nums)
{
if(flag & e) //为1
{
ret1^=e;
}
else//为0
{
ret2 ^= e;
}
}
return {ret1,ret2};//隐式类型转换
}6、题6 判定字符是否唯一 :
面试题 01.01. 判定字符是否唯一 - 力扣(LeetCode)
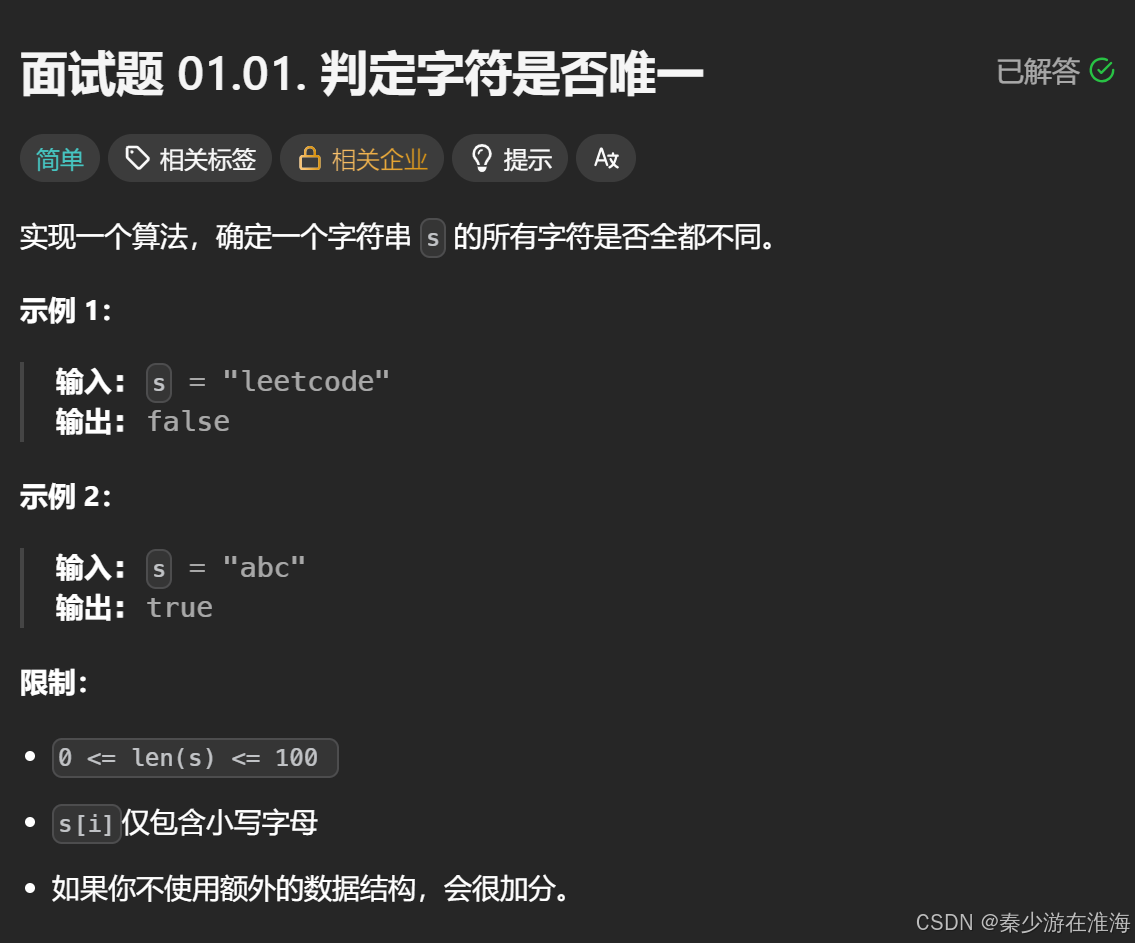
解法一:哈希表
判断字符串中的字符是否相同,可以借助于哈希表;
从前往后将遇到的字符扔进哈希表中,同时需要判断该字符是否已经在哈希表中,若存在就需要return false ,不存在并且遍历完该字符才 return true;
而实现hash 我们可以使用unordered_map 也可以使用 数组;由于本题的s 中只包含小写字母,我们可以只用大小为26 的数组,通过下标映射来实现hash;其实在这基础上还可以进行空间优化,利用比特位来记录信息,即位图思想;
解法二:位图
Q:为什么可以借助于位图的思想?
- 因为单独的一个int 变量有 32 位,可以让最右边的比特位(认为最右边的比特位为0号位)来代表'a' ……而比特位中要么是0要么是1,我们便可以利用0来表示该字符没有出现,用1来表示该字符出现过;
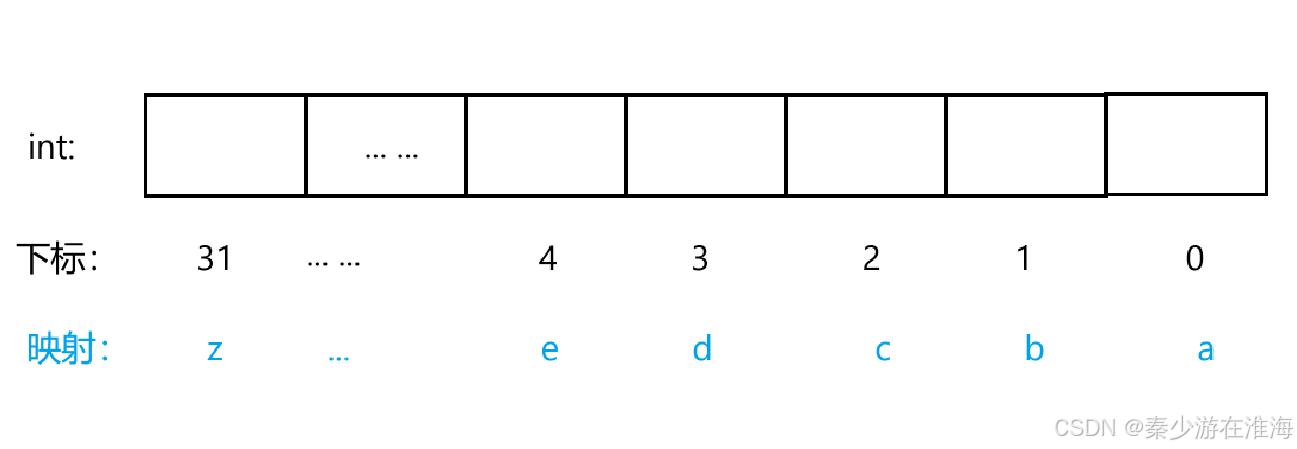
其实位图就是hash的思想,只不过在空间上,利用位图用1byte 就可以解决;
在遍历字符串的时候,会去位图中查询某个字符是否存在即该比特位是否为1,以及将某个比特位修改为1;
假设位图为 n , 某个字符为 s[i]
- 查询某个字符是否存在(对应的比特位是否为1): (1<<(s[i]-'a'))&n== n,如果相等则说明是s[i] 已然存在;不相等则说明s[i] 不存在;
- 将某个比特位修改为1:n = (1<<(s[i]-'a')) | n
每遍历到一个字符均会执行以上两个操作;此处还有一个优化代码的思想:鸽巢原理(抽屉思想)
Q:什么是鸽巢原理?
- 如果有11只鸽子和10个鸽巢,其中一定有一个鸽巢中的鸽子数量大于1;
而本题中,我们一共有26个英文字母,当我们的字符串的长度大于26的时候,就一定就会有重复的字符;所以此处的小优化是:在使用位图之前先判断一下这个字符串的长度是否大于26,如果大于26直接return false;
参考代码:
bool isUnique(string astr)
{
//小优化,如果字符串的长度大于26,直接返回false
if(astr.size() >26) return false;
//利用位图
int n = 0;
for(auto e:astr)
{
//先判断在位图中该字符是否已经存在,如果已经存在返回false
if((1<<(e-'a'))&n) return false;
else
{
//将对应字符的比特位修改为1
n = (1<<(e-'a'))|n;
}
}
//走到这里都没有返回说明该字符串中的字符均是唯一的
return true;
}7、题7 丢失的数字:

解法一:暴力遍历
先对nums 进行排序,然后遍历数据,看前一个数据与当前数据是否相差为1即可;
解法二:哈希表
将nums 中的数据均放入hash表中,看哪一个位置上少了数据;
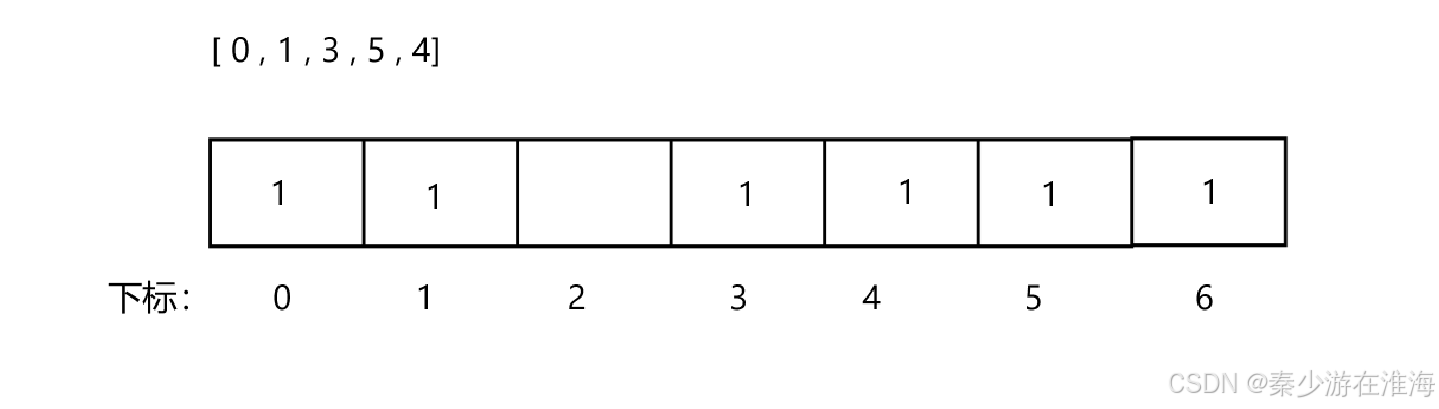
解法三:二分
二分的核心在于二段性,因为所给的数组nums 中缺少一个数,而nums 中的数据是乱序的,所以先排序;从下标与数据的对应关系上来看,nums 中的数据具有二段性,一段是下标与数据一一对应,一段是下标与数据不对应;我们只需要找到“下标与数据不对应区间”的左下标即可;
因为需要避免只有两个数据的时候二分出现死循环,就需要让所求的的中间结点偏左,即 int mid = left +(right-left )/2; 当mid 处在第一段的时候,left = mid+1; 当 mid 处于第二段的时候,right = mid;
参考代码:
int missingNumber(vector<int>& nums)
{
//二分
sort(nums.begin() , nums.end());
int n = nums.size();
int left = 0, right = n;
while(left < right)
{
int mid = left + (right-left)/2;
if(mid == nums[mid]) left = mid+1;
else right = mid;
}
return left;
}解法四:高斯求和
((首项+末项)*项数)/2 就可以求出区间[0,n] 中数据的总和,然后再减去0+1+...+n 的和,所得到的结果就是缺少的那个数;
参考代码:
int missingNumber(vector<int>& nums)
{
//高斯求和
int sum1 = 0 , n = nums.size();
for(auto e : nums) sum1+=e;
int sum2 = ((0+n)*(n+1))/2;
return sum2-sum1;
}解法五:位运算
利用按位异或的运算律:

相同的数据按位异或的结果为0,而一个数与0按位异或其结果还是这个数本身;那么我们利用这个特点,将nums 中的数据与 0~n 的数据按位异或,那么最后得到的数就是nums 中缺少的数;
参考代码:
int missingNumber(vector<int>& nums)
{
//位运算
int ret = 0;
for(auto e: nums) ret^=e;
for(int i = 0;i<=nums.size();i++) ret^=i;
return ret;
}8、题8 两整数之和:
如果这道题在笔试中遇见,直接return a+b 即可;因为在笔试场中只要能 ac 这道题就可以了;
解法:
像这种不能使用加法或者减法但又要计算加、减的题,大概率是用位运算来解决;其中,如果算 a+b ,我们可以利用按位异或,因为按位异或可以看作是“无进位相加”;那我们就只需要处理进位问题就可以了;
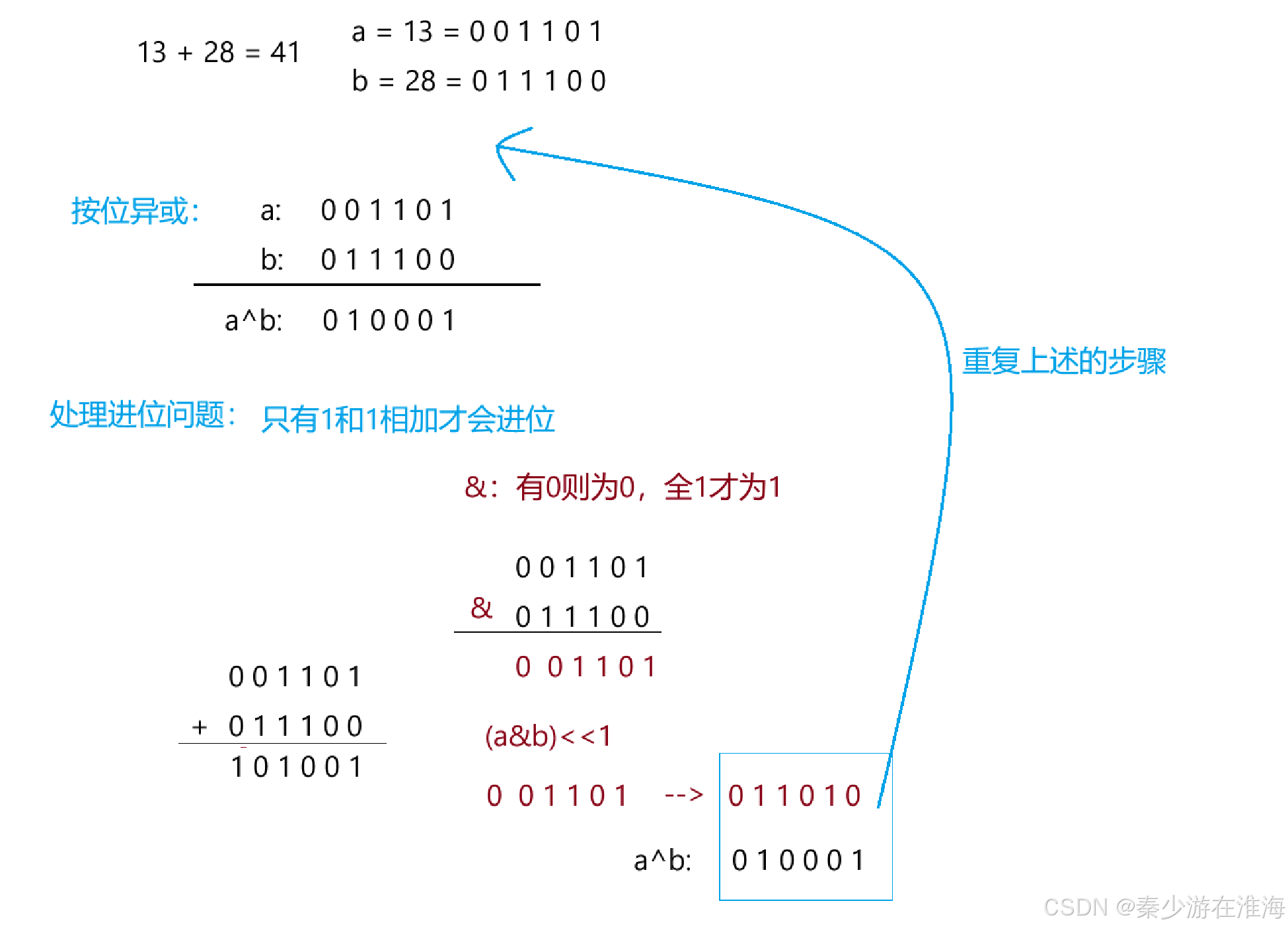
(a&b)<<1 相当于就是拿到了进位,而 a^b 就是“非进位相加”的部分;所以只要将(a&b)<<1 与 a^b相加就可以了,而这样的话又回到了“相加”的逻辑中……于是就要重复上述步骤;
尝试一下,一直按位异或、按位与左移下去会怎样:
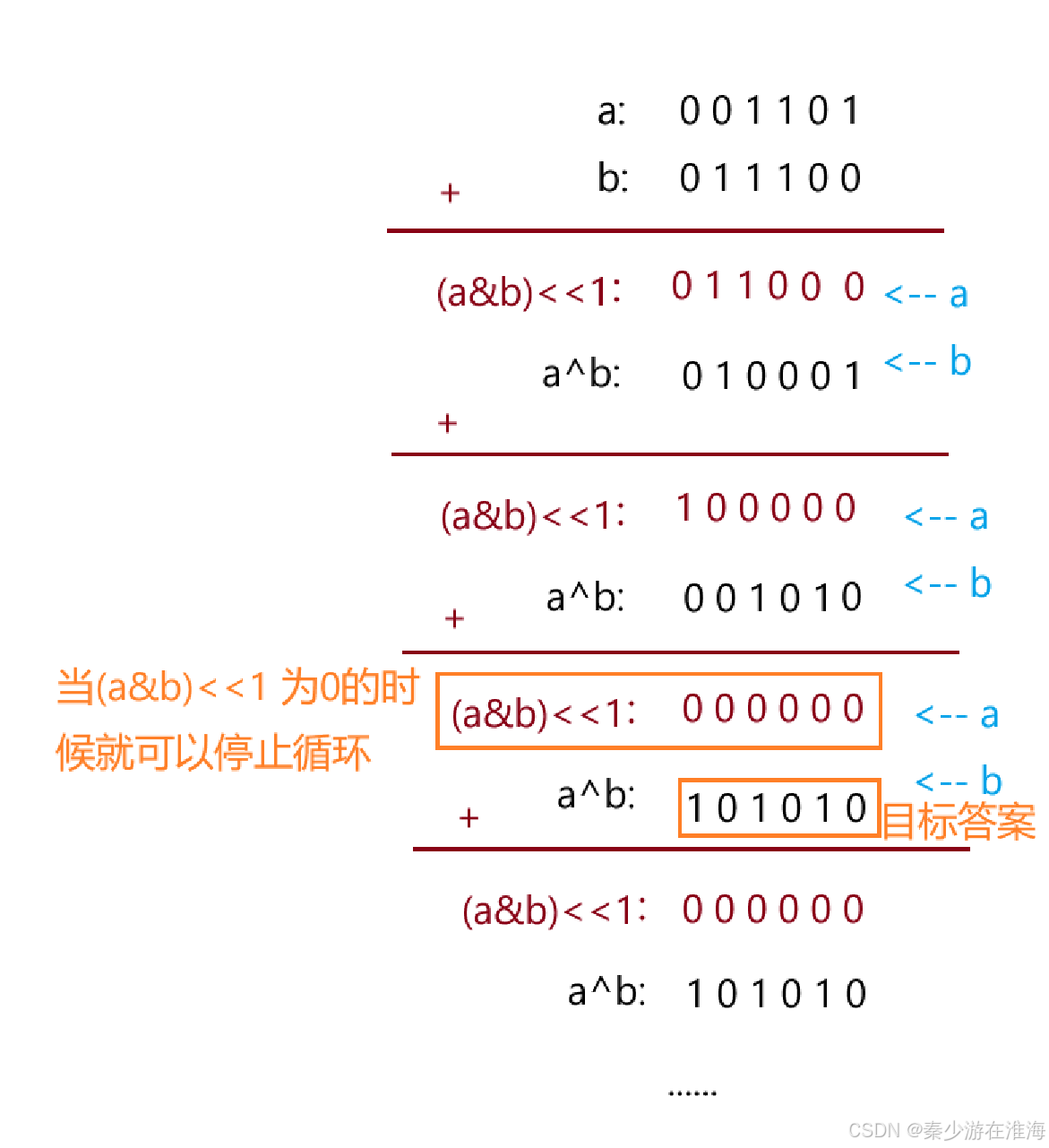
所以我们的循环条件是:(a&b)<<1 != 0 ; 当循环结束的时候,a^b 就是最后的答案;
代码:
int getSum(int a, int b)
{
//^ : 无进位相加
//(a&b)<<1 来处理进位
while(b)
{
int z = a;//保存原先的a
a = a^b;//无进位相加
b = (z&b)<<1;//进位
}
return a;
}这个代码可以成功运行,但是仍然存在一个小 bug , 如果(a&b) 的结果是-1(所有的比特位均为1) ,那么左移操作 << 是未定义的;
-
C语言标准(C11 §6.5.7/4)明确指出:
If
E1has a signed type and negative value, the behavior ofE1 << E2is undefined.
(如果E1是有符号类型且为负值,则E1 << E2的行为未定义。)
需要注意的是,负数在内存中以补码形式存储(最高位是符号位 1);左移操作会将符号位一同左移,并填充低位为 0。例如:
int8_t a = -1; // 二进制: 11111111
a << 1; // 结果: 11111110(即 -2,符合预期?)注:左移可能改变符号位(如 1 被移出,新符号位可能是 0),导致:
- 逻辑矛盾:结果变为正数
- 数值超出有符号整型的表示范围(溢出风险)
- 标准委员会认为这种场景的语义无法统一且存在风险,故直接定义为未定义行为。
所以此处应该在 (a&b)<<1 的时候使用无符号整形;
参考代码:
int getSum(int a, int b)
{
//^ : 无进位相加
//(a&b)<<1 来处理进位
while(b)
{
int z = a;//保存原先的a
a = a^b;//无进位相加
//进位,使用无符号
unsigned int carry = (unsigned int)(z&b)<<1;
b = carry;
}
return a;
}9、题9 只出现一次的数字 II :
137. 只出现一次的数字 II - 力扣(LeetCode)
解法:位运算
因为nums 中的数据均是奇数个,我们就难以单纯地使用按位异或进行区分;
将所有数任意比特位可能会出现以下四种情况:
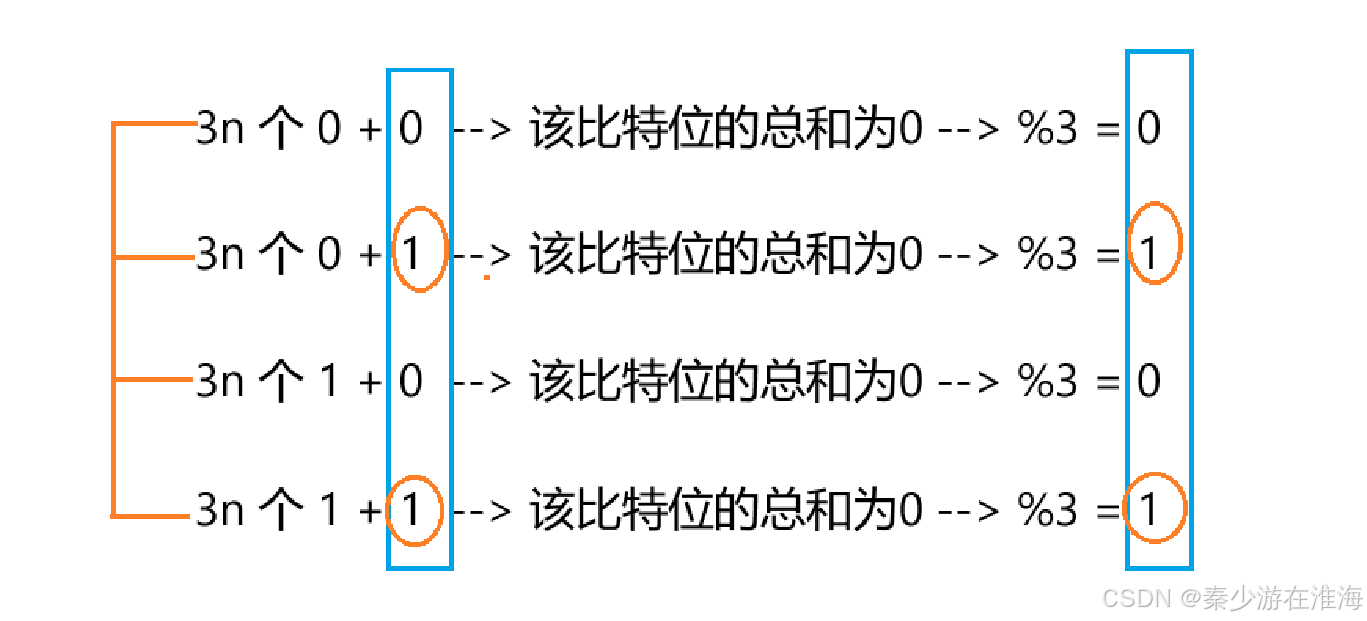
可以发现,当这个比特位所有数之和 %3 为1 的时候,这个单独的数比特位上为1;因为其他数均是3个,那么无论比特位为多少,其比特位之和均可以被 3 整除;
显然,基于以上这个特点,我们可以依次将所有数 0~32 位比特位相加并 %3 , 如果所得结果为1,那么单独的数中该比特位就为1;如果为0,那么单独的这个数的比特位就为0……只要得到了单独的这个数的每一个比特位,那么就知道了这个单独的数为多少;
需要注意的是,本题还可以进行扩展:如果在一个数组中,一个数出现了1次,其他数出现了n 次,求这个只出现了一次的数;
- 同样地,依次取所有数的每一位相加,然后 %n , 将所得结果填入对应的位置中,当32个位置均填充完,该数便为目标数;
参考代码:
int singleNumber(vector<int>& nums)
{
int ret = 0;
//让所有数的比特位相加
for(int i = 0;i<32;i++)
{
int tmp = 0;
for(auto e: nums)
{
if((1<<i)&e) tmp++;
}
tmp%=3;
//如果tmp 为1,就将ret 的第i 位修改为1,| :有1则为1,全0才为0
if(tmp == 1) ret |= (1<<i);
}
return ret;
}10、题10 消失的两个数字:
面试题 17.19. 消失的两个数字 - 力扣(LeetCode)
解法:位运算
这道题与本篇博文的第五题很像,所以就不做过多赘述;
因为数据是从 1~N , 所以我们就天然地可以认为数组 nums 中的数据有两个只出现一次的数,然后剩下的数均出现了两次;那么我们可以先让所有的数进行按位异或,然后找到结果中最右端的1作为将nums 分为两部分的依据;然后对这两个部分的数据分别进行按位异或,最后的结果就是目标数据;
参考代码1:
vector<int> missingTwo(vector<int>& nums)
{
int n = nums.size();
//1、将所有的数据进行按位异或
int tmp = 0;
for(int i = 1;i<=(n+2);i++) tmp^=i;
for(auto e: nums) tmp^=e;
//2、找到tmp 中最右端的1,作为划分的依据
tmp = tmp & (-tmp);
int ret1 = 0, ret2 = 0;
//3、再次遍历数组,分成两部分进行按位异或
for(auto e: nums)
{
if(e&tmp) ret1^=e;
else ret2^=e;
}
for(int i = 1;i<=(n+2);i++)
{
if(i&tmp) ret1^=i;
else ret2^=i;
}
return {ret1,ret2};
}我们此处找最右端的1直接用 n&(-n) 来解决,实际上也可以用循环,来知道第几位是1;然后下面在进行按位异或的时候就需要进行移位;这也是一种思路;
参考代码2:
vector<int> missingTwo(vector<int>& nums)
{
int n = nums.size();
//1、将所有的数据进行按位异或
int tmp = 0;
for(int i = 1;i<=(n+2);i++) tmp^=i;
for(auto e: nums) tmp^=e;
//2、找到tmp 中最右端的1,作为划分的依据
int index = 0;
while(1)
{
if(tmp&(1<<index)) break;
index++;
}
//3、再次遍历数组,分成两部分进行按位异或
int ret1 = 0, ret2 = 0;
for(auto e: nums)
{
if(e&(1<<index)) ret1^=e;
else ret2^=e;
}
for(int i = 1;i<=(n+2);i++)
{
if(i&(1<<index)) ret1^=i;
else ret2^=i;
}
return {ret1,ret2};
}总结
- 给一个数 n ,确定它的二进制表示中第 x 位是 0 还是 1 : (1<<x)&n 或者 (n>>x)&1
- 将一个数 n 的二进制表示的第 x 位修改为1: n = (1<<x)|n , 可以简写为 n|=(1<<x);
- 将一个数n 的二进制表示的第 x 为修改为0 :n = (~(1<<x))&n , 可以简写为:n&=(~(1<<x))
- 提取一个数 n 的二进制表示中最右侧的1 :n&(-n)
- 干掉一个数 n 二进制表示中最右侧的1 : n = n&(n-1) , 简写为: n &=(n-1);
- 强烈建议在复杂的表达式中大量使用括号 ( ) 来明确指定运算顺序。这不仅能避免错误,还能大大提高代码的可读性。
- 按位异运算的运算律

 常见位运算总结及LeetCode题解
常见位运算总结及LeetCode题解





















 805
805

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








