系列文章目录
leetcode - 双指针问题_leetcode双指针题目-优快云博客
leetcode - 滑动窗口问题集_leetcode 滑动窗口-优快云博客
目录
前言
路漫漫其修远兮，吾将上下而求索；
大家可以先尝试自己做一下喔~
斐波那契数列模型
- 1137. 第 N 个泰波那契数 - 力扣（LeetCode）
- 面试题 08.01. 三步问题 - 力扣（LeetCode）
- 746. 使用最小花费爬楼梯 - 力扣（LeetCode）
- 91. 解码方法 - 力扣（LeetCode）
1、题1 第 N 个泰波那契数 ：
1137. 第 N 个泰波那契数 - 力扣（LeetCode）
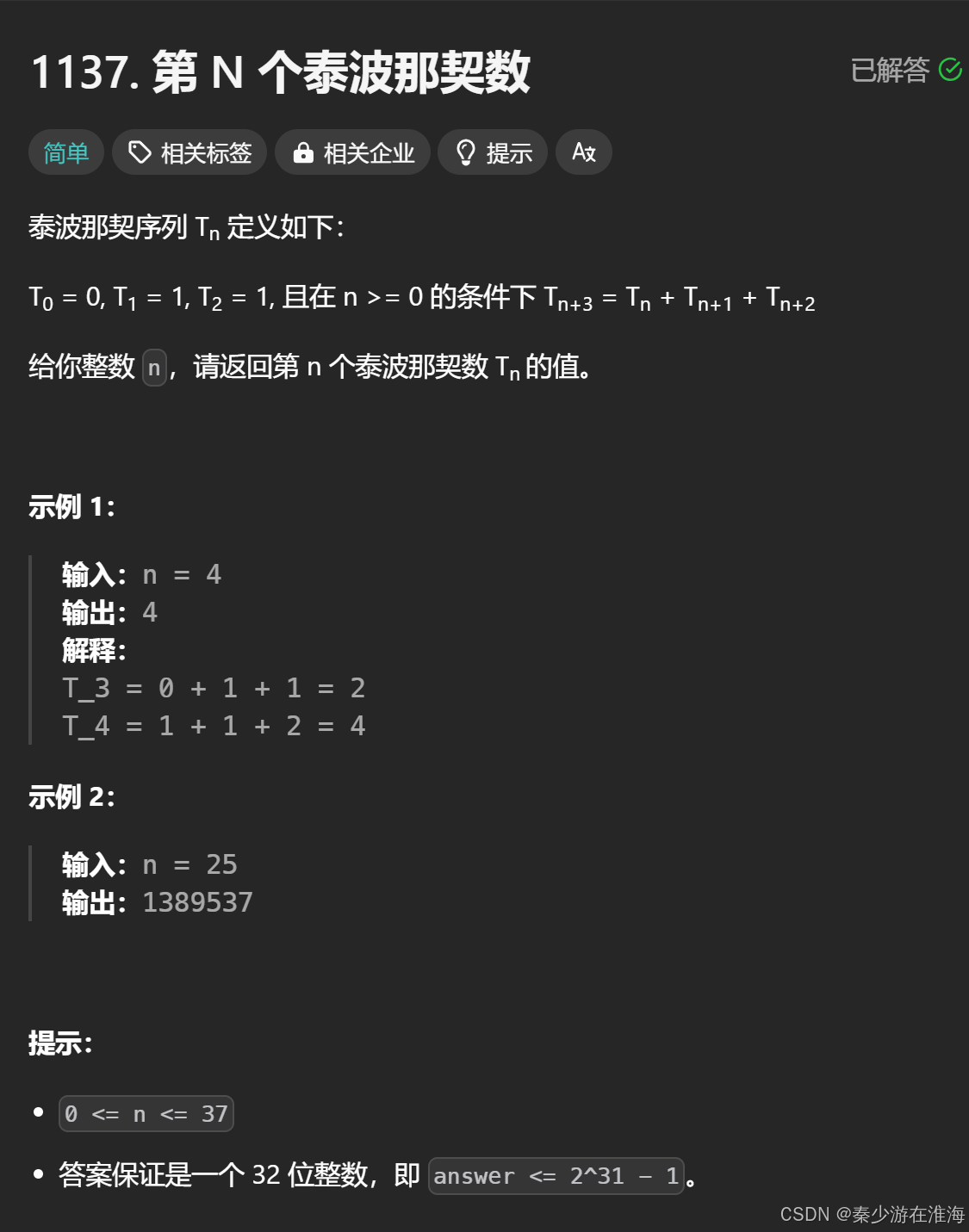
思考：
可以将泰波那契数看作是斐波那契数的加强版；
根据题意可知第n个泰波那契等于其前三个泰波那契数之和；
解法一：动态规划
动态规划的做题流程，一般会定义一个dp 表（dp 表通常是一个一维数组或者二维数组）；一维数组的情况：先创建一个一维数组，该数组通常被称为dp 表，接下来就是填dp 表，其中的某一个值可能就是最后的结果；
我们可以使用动态规划来解决这道题，五个步骤：
1、确定一个动态表达式
2、根据该动态表达式来推导状态转移方程
3、初始化
4、填表顺序
5、返回值
a、状态表示
Q1： 什么是状态表示？
- dp 表中某一个位置所代表的含义；eg.dp[0] 存了一个值a,那么值a 便会代表一个特殊的含义，其中此含义就是状态表示；
Q2：状态表示是怎么样来的？
一般有三种方式可以来确定：
- 1、题目怎么要求，我们就怎么定义状态表示
- 2、经验 + 题目要求
- 3、分析题目的过程中发现重复的子问题（再将重复的子问题抽象为状态表达式）
注：在本题中可以直接按照题干的要求去定义一个状态表示；本题的目标：返回第n个泰波那契数；
我们可以搞一个dp 表，让dp[0] 表示第0个泰波那契数，dp[1] 表示第1个泰波那契数……dp[i] 表示第i 个泰波那契数……我们只需要返回第n 个泰波那契数，即返回 dp[n];
b、状态转移方程
在本题中，我们需要思考的是：dp[i] 怎么求来？
推导状态转移方程：1、用之前或者之后的状态推导得到dp[i] 的值 2、根据最近的一步来划分问题
本题十分明显由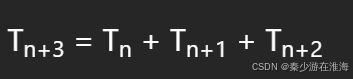
可得：Tn = Tn-1 + Tn-2 + Tn-3 ；故而本题的状态转移方程为：dp[i] = dp[i-1] + dp[i-2] + dp[i-3];
c、初始化
初始化的含义：保证填dp表（根据状态转移方程来调表）的时候不会发生越界；
Q1：为什么要保证不越界？
- 倘若用此处的状态转移方程：dp[i] = dp[i-1] + dp[i-2] + dp[i-3]; 直接填表，那么 dp[0] = dp[-1] + dp[-2] + dp[-3] ，而 dp[-1] ，dp[-2] ，dp[-3] 就是越界访问；本题中的dp[0] 、dp[1]、dp[2]使用状态转移方程的时候均会发越界，所以这三个值需要单独进行初始化；而如何初始化取决于题干；
在本题中：
d、填表顺序
Q：为什么要研究填表顺序？
- 为保证填写当前状态的时候所需要的状态已经计算好了；
在本题中，因为dp[i] = dp[i-1] + dp[i-2] + dp[i-3]，即填表的时候需要借助于其前三个数据，所以填表顺序为从左往右；
d、返回值
返回结果： 结合题目要求+状态表示
本题干：
，所以我们返回 dp[n] 即可；
参考代码：
int tribonacci(int n)
{
//边界情况处理
if(n==0) return 0;
else if(n==1 || n==2) return 1;
//创建一维dp
//状态表示：dp[i]表示第i个泰波那契数
//状态转移方程：dp[i] = dp[i-1] + dp[i-2] + dp[i-3]
//初始化： dp[0]= 0 , dp[1] =1, dp[2] = 1;
//填表顺序： 从左往右
//返回值：dp[n]
vector<int> dp(n+1);
//初始化
dp[0]= 0 , dp[1] =1, dp[2] = 1;
//填表
for(int i = 3;i<=n;i++)
{
//状态转移方程
dp[i] = dp[i-1] + dp[i-2] + dp[i-3];
}
//返回结果
return dp[n];
}解法二：空间优化版本
注：此处空间优化的技巧只会在这道题以及接下来的背包问题中可用；
关于动态规划的空间优化，一般都是用流动数组的形式来优化；可以将时间复杂度为O(N^2)的动态规划优化成时间复杂度为O(N)，将时间复杂度为O(N)的动态规划优化成时间复杂度为O(1)；
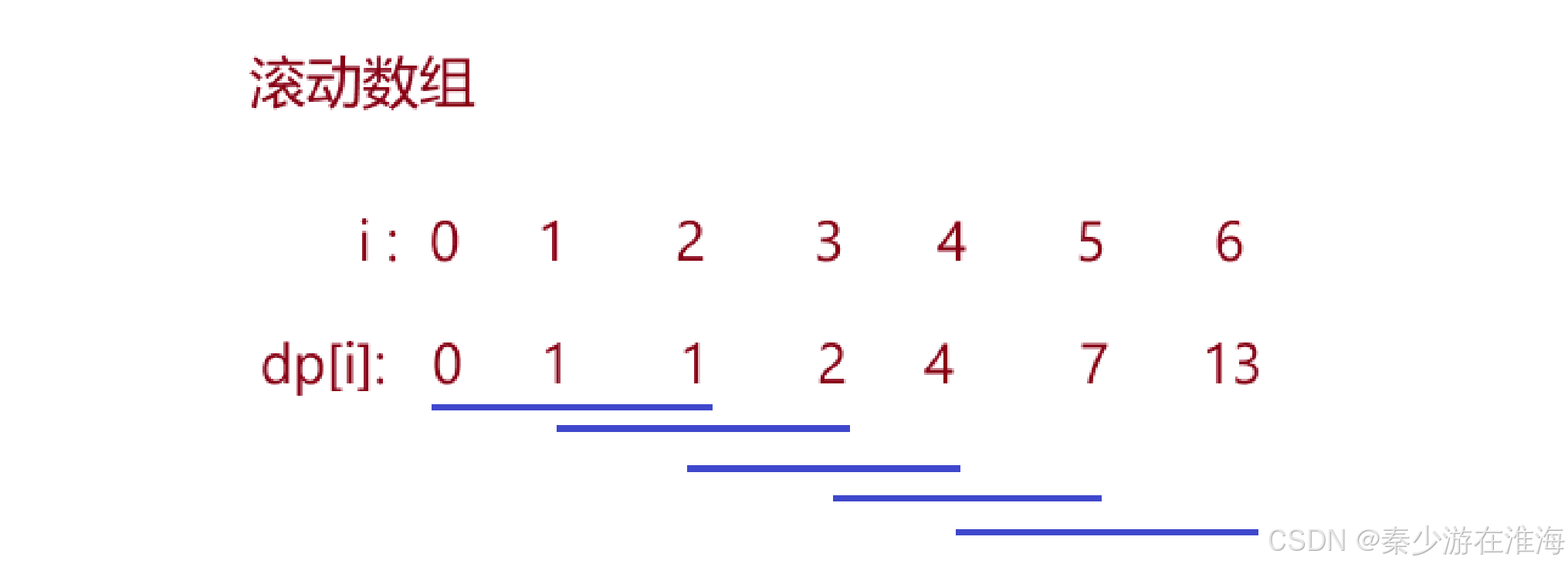
可以发现，在求某一状态时，仅需要该状态前三个状态就可以求得到本状态；当我们依次从左往右求dp[i] 的时候，dp数组中太靠前的数据反而用不到，显然用不到的数据可以省去的。仅用该数组中有效的若干个状态便可以解决，像这样的情况，我们都可以用滚动数组来解决；创建三个变量进行”流动“，以维护所求状态的前三个状态；
Q：明明是利用变量在滚动的，为什么叫做”滚动数组“？
”滚动数组“只是一个名字而已，取这个名称只是为了统一叫法；
注：三个变量，在实现的时候还可以定义为 int[3] 的数组，但是我们没有必要这么做，因为这样实现起来有点麻烦还没有用三个变量来实现得“利落”；
图解如下：
细节问题：
赋值时的方向问题，是从左向右赋值还是从右往左赋值呢？
所以应该选择从左往右赋值；
参考代码：
int tribonacci(int n)
{
if(n==0) return 0;
else if(n==1 || n==2) return 1;
//空间优化 - 滚动数组
int a = 0 , b = 1 , c = 1 , d = 0 ;
for(int i = 3;i<=n;i++)
{
d= a+b+c;
a = b;
b = c;
c = d;
}
return d;
}2、题2 三步问题：
面试题 08.01. 三步问题 - 力扣（LeetCode）
注：1000000007 可以写作 1e9+7
解法: 动态规划
动态规划的五个步骤：
1、确定状态表示
2、根据该状态表示确定状态转移方程
3、初始化（以确保在填表的时候不会越界）
4、确实填表顺序
5、返回值
1、状态表示
一般有三种方式可以来确定状态表示：
- 1、题目怎么要求，我们就怎么定义状态表示
- 2、经验 + 题目要求
- 3、分析题目的过程中发现重复的子问题（再将重复的子问题抽象为状态表达式）
在推导此题的时候发现本题是一个线性dp 模型，求本题的状态表示可以先根据我们的 经验(以 i 位置为结尾) + 题目要求（计算到达第i 个台阶的方案数）；
状态表示：dp[i] 表示到第 i 个位置时，一共有多少种方法；
2、状态转移方程
推导状态转移方程：1、用之前或者之后的状态推导得到dp[i] 的值 2、根据最近的一步来划分问题
经验：想办法让i 位置之前或者之后的状态来表示 dp[i] ；
从左往右到达 i 位置有三种情况：
dp[i] 分三种情况来讨论：
从(i-3) 这个位置跳三个台阶 到 i 位置上，首先就需要先到 (i-3) 这个位置上；假设到 (i-3) 这个位置上有 x 种方法，那么在到 (i-3)的方法数上这一步就是（i-3)->i 的方法数，即从 (i-3)->i 的方法数是 0->(i->3) 方法数 x ；
而从 0->(i-3) 位置的方法数为dp[i-3]
同理：
即dp[i] = dp[i-1] + dp[i-2] + dp[i-3];
3、初始化
初始化的目的：保证填dp表（根据状态转移方程来调表）的时候不会发生越界；
在填dp[1] dp[2] dp[3] 的时候由于下标相减，会访问到 -1,-2,-3 下标的非法空间，为了避免越界访问的出现，此处需要初始化dp[1] dp[2] dp[3]；
dp[1] = 1 , dp[2] = 2 , p[3] = 4;
4、填表顺序
在本题中，只有将dp 前面的数据算出来了以后才可以算后面的，故而填表顺序为从左往右
5、返回值；
结合题干要求：
，所以返回值为dp[n]
参考代码：
int waysToStep(int n)
{
//创建一维数组dp
//状态表示： dp[i]到第i 阶台阶的方法数 状态转移方程：dp[i] = dp[i-1]+d[i-2] +dp[i-3]
//初始化：dp[1] = 1, dp[2] = 2, dp[3] = 4
//填表顺序：从左往右 返回值 ；dp[n]
//边界情况处理
const int MOD = 1e9+7;
if(n==1 || n==2) return n;
else if(n==3) return 4;
//dp
vector<int> dp(n+1);
//初始化
dp[1] =1 , dp[2] =2, dp[3] = 4;
for(int i = 4 ; i<=n;i++)
{
dp[i] = ((dp[i-1]+dp[i-2])%MOD +dp[i-3]) % MOD;
}
//返回
return dp[n];
}3、题3 使用最小花费爬楼梯：
首先我们需要明确题意：我们可以向上爬一阶也可以向上爬两步，但是需要支付从第i 个台阶向上爬的费用；我们需要计算得到到达楼梯顶部的最低花费；而我们选择开始，可以从下标为0的台阶开始，也可以从下标为1的台阶开始爬；
首先我们需要弄清楚的是，楼顶在什么地方？
先观察一下例子：
所以我们的楼顶为，最后一个数据的下一个位置；
解法一：动态规划(以某一个位置为结尾)
动态规划的五个步骤
1、确定一个状态表达式
2、根据该动态表达式来推导状态转移方程
3、初始化
4、填表顺序
5、返回值
1、状态表示
一般有三种方式可以来确定状态表示：
- 1、题目怎么要求，我们就怎么定义状态表示
- 2、经验 + 题目要求
- 3、分析题目的过程中发现重复的子问题（再将重复的子问题抽象为状态表达式）
根据经验 + 题干要求
注：经验：像一维数组dp 一般分为两种，一种是以某一个位置为结尾；一种是以某一个位置为开头；
因为本题要找到达楼顶的最小花费，那么以i位置为结尾就相当于到达了第 i 个位置的最小花费；
那么dp[i] : 到达 i 位置的最小花费
2、状态转移方程
推导状态转移方程：1、用之前或者之后的状态推导得到dp[i] 的值 2、根据最近的一步来划分问题
根据题意，我们需要从前往后走，也就是说倘若我们要到达 i 位置就需要分为两种情况：
在本题中，到达哪一个台阶就需要支付相应的费用，如下：
到达 i 台阶有两种方式，我们选择花费最小的就可以了；
而对于先达到 (i-1) 位置，再走一步到达 i 位置，就需要我们先计算出走到 (i-1) 位置上的最小花费再加上 (i-1) 上的花费就是到达 i 的费用；--> dp[i] = dp[i-1] + cost[i-1];
而对于先到达 (i-2) 位置，再走两步到达 i 位置，需要我们先计算出走到 (i-2) 位置上的最小花费，再加上 (i-2) 上的花费就是到达 i 的费用； --> dp[i] = dp[i-2] + cost[i-2];
综上：dp[i] = min(dp[i-1]+cost[i-1] , dp[i-2] + cost[i-2]);
很多dp 问题均是可以利用这种方式来推导出状态转移方程：
主线（引导我们推导状态转移方程的主线）：用之前或者之后的状态来推导dp[i] 的值，其中状态转移的时候很好的经验：根据最近的一步来划分问题；（可以分情况）
3、初始化
初始化的目的：保证填dp表（根据状态转移方程来调表）的时候不会发生越界；
因为状态转移方程：dp[i] = min(dp[i-1]+cost[i-1] , dp[i-2] + cost[i-2]); 若 i 为0、1则就会发生越界访问，所以需要初始化 dp[0],dp[1] ;
即 dp[0] = 0 , dp[1] = 0;
4、填表顺序
填表顺序的确定是为了保证我们在填dp[i] 这个数的时候，dp[i-1] 以及 dp[i-2] 已经被计算出来了，那么填表顺序就是：从左往右；
5、返回值
根据题目要求：
，所以我们返回 dp[n] 就可以了；
参考代码：
int minCostClimbingStairs(vector<int>& cost)
{
int n = cost.size();
//创建一维数组dp
//状态表示：dp[i]:表示到达第i阶的最小花费 状态转移方程：dp[i] = min(dp[i-1]+cost[i-1] , dp[i-2]+cost[i-2]);
//初始化：dp[0] = 0, dp[1] = 0;
//填表顺序：从左往右 返回值：dp[n]
vector<int> dp(n+1);
//初始化
dp[0] = 0, dp[1] = 0;
//填表
for(int i = 2;i<=n;i++)
{
dp[i] = min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2]);
}
return dp[n];
}解法二：动态规划(以某一个位置为开头)
解法一是以某一个位置为结尾，我们还可以以某一个位置为开头；
同样的，五个步骤；
1、状态表示
一般有三种方式可以来确定状态表示：
- 1、题目怎么要求，我们就怎么定义状态表示
- 2、经验 + 题目要求
- 3、分析题目的过程中发现重复的子问题（再将重复的子问题抽象为状态表达式）
dp[i] ：从 i 位置出发，到达楼顶的最小花费；
2、状态转移方程
推导状态转移方程：1、用之前或者之后的状态推导得到dp[i] 的值 2、根据最近的一步来划分问题
当我们位于 i 位置的时候，可以向前走一步到 i+1 ，也可以向前走两步到 i+2 ：
从i 位置需要支付 cost[i] 的费用，有两种走法，选择费用最小的那一种就可以了；所以状态转移方程为： dp[i] = min(dp[i+1] , dp[i+2]) + cost[i];
3、初始化
初始化的目的就是为了保证在填表的时候不会发生越界访问；因为状态转移方程中会用到 dp[i+1]、dp[i+2] ，即i+1<n ， i+2<n ,所以我们需要初始化 dp[n-1] 和 dp[i-2]
- 而从(n-1) 的位置到达楼顶就只能走一步，即花费cost[n-1] 的费用到达楼顶；
- 而从 (n-2) 的位置到达楼顶，有两种走法，一种是走两步到楼顶，另一种是先走到(n-1) 的位置上，然后再走一步到达楼顶,即 dp[n-2] = min(cost[n-2] , cost[n-2]+dp[n-1]) ，显然cost[n-2]一定小于 cost[n-2]+dp[n-1] ， 所以dp[n-2] 初始化为 cost[n-2] 就可以了；
dp[n-1] = cost[n-1] ，dp[n-2] = cost[n-2];
4、填表顺序
确定填表顺序的目的是为了保证在填表的时候，所要依据的状态已经存在了；即在填写dp[i] 的时候要保证 dp[i+1] 以及 dp[i+2] 已经填好了，故而填表顺序为从右往左；
5、返回值
根据题目要求，以及状态转移方程来确定；
因为求最初是从下标为0或者下标为1的地方开始达到楼顶的最小费用，所以应该返回这两种情况下花费的最小值；
参考代码：
int minCostClimbingStairs(vector<int>& cost)
{
int n = cost.size();
//dp[i]:从i 位置开始，向后走到达楼顶的最小花费
//状态转移方程： dp[i] = min(dp[i+1] , dp[i+2]) + cost[i]
//初始化： dp[n-1] = cost[n-1] , dp[n-2] = cost[n-2];
//填表顺序：从右往左 返回值：min(dp[0], dp[1]);
vector<int> dp(n);
//初始化
dp[n-1] = cost[n-1] , dp[n-2] = cost[n-2];
//填表
for(int i = n-3;i>=0;i--)
{
dp[i] = min(dp[i+1] , dp[i+2]) + cost[i];
}
return min(dp[0] , dp[1]);
}一维线性dp:一般是由某个位置为结束或者某个位置为起点；如果以此定义状态表达式的时候能够推导出正确的状态转移方程，可以解决问题，那就说明该状态转移方程是正确的；而如果定义的这个状态表示没有办法推导出状态转移方程，没办法拿到最终的结果，那就说明该状态表示就是错的；(也就是说状态表示也会定义错，同时状态表示可以定义多个)；
4、题4 解码方法：
思考：
将 1-26 的数字转换成26 个字母；
解法：动态规划
同样地，利用动态规划来解决问题有5个步骤：
1、根据题干写出状态表示
2、推导状态转移方程
3、初始化
4、填表顺序
5、返回值
1、状态表示：
一般有三种方式可以来确定状态表示：
- 1、题目怎么要求，我们就怎么定义状态表示
- 2、经验 + 题目要求
- 3、分析题目的过程中发现重复的子问题（再将重复的子问题抽象为状态表达式）
因为我们是从左往右依次解码，所以我们的dp 是一个线性的dp。这种dp 模型一般是根据经验+题目要求来定义状态的；结合本题，若以某一个位置为结尾，我们是需要解码这一串数字，那么到某一个位置为结尾的话，从左往右正好可以解码到此位置；
如上图，从 0 位置开始一直解码到 i 位置；题干求的是解码方法的总数，故而我们的状态转移方程可以定义为：从 0 到 i 位置，即以下标 i 为结尾时，所有解码方案的总数；
那么 dp[1] 表示的是前两个位置，也就是解码到下标为 1 的位置的解码方案的总数
dp[i+1] 表示：i+2 个位置，也就是解码到下标为 i+1 的位置的解码方案总数；
状态表示：dp[i]: 以 i 位置结束时，解码方法的总数
2、状态转移方程
推导状态转移方程：1、用之前或者之后的状态推导得到dp[i] 的值 2、根据最近的一步来划分问题
根据最后一步的划分来解决问题；
如若我们的状态表示是以 i 位置为结尾的解码方式的总数，那么最近的一步应该是我们正好解码至 i 位置，而解码到 i 位置又存在两种情况；第一种情况是让 i 位置单独去解码；第二种情况就是让i 位置与 (i-1) 的位置结合，然后一起去解码；
所以，我们的最后一步可以划分为：
根据划分的情况来推导我们的状态转移方程：
所以 dp[i] = dp[s[i] 单独解码] + dp[s[i-1] 与 s[i] 结合后再解码]；
3、初始化
初始化的目的就是为了让我们在填表的时候不会出现越界问题；在上述的状态转移方程中，我们会用到 dp[i-2] 、dp[i-1] 所以我们需要初始化 dp[0]、dp[1] ；
- 以0 下标位置为结尾，只需要判断 0 下标中的数是不是0就行了，是0 则初始化为0，不是0 则初始化为1；
- 在下标0可以单独解码得情况下，先判断 下标为1 中的字符是否可以单独进行解码，如果可以则为 dp[0] , 如果不可以则为 0; 然后需要判断下标 0 与 下标1上的两个字符是否可以结合一起解码，如果解码成功则为dp[1]+1;如果解码失败则为 0;
最后 dp[i] = dp[s[i] 单独解码] + dp[s[i-1] 与 s[i] 结合后再解码]；
本题的初始化需要根据题目来分析；
4、填表顺序
求dp[i] 的时候需要知道dp[i-1] 或者 dp[i-2] 的值，由此我们可以得知我们的填表顺序是从左往右的；
5、返回值
根据状态表示以及题干要求(求整个字符串的解码方案总数)来；
dp[i] : i 位置结束时，解码方案的总数
也就是说，我们要解码到最后一个位置，而最后一个字符的下标为 n-1 ,故而我们需要返回 dp[n-1]
参考代码：
int numDecodings(string s)
{
int n = s.size();
//dp[i]: 以 i 位置结束的解码方案的总数
//状态转移方程需要分情况讨论，4种情况
//初始化：也需要讨论 填表顺序：从左往右 返回值 :dp[n-1]
vector<int> dp(n);
//初始化
dp[0] = s[0]== '0' ? 0: 1;
//边界情况处理
if(n==1) return dp[0];
//先判断s[1] 是否可以单独解码
if(s[0]!='0' && s[1]!= '0') dp[1]= 1;
//再判断 s[0] 与 s[1] 是否可以结合解码
int t = (s[0]-'0')*10 + (s[1]-'0');
if(t>=10 && t<=26) dp[1]+=1;
//填表
for(int i = 2;i<n;i++)
{
//判断单个是否解码成功
if(s[i]!='0') dp[i] = dp[i-1];
else dp[i] = 0;
//再判断 i-1 与 i 结合解码是否成功
int t = (s[i-1]-'0')*10 + (s[i]-'0');
if(t>=10 && t<=26) dp[i]+=dp[i-2];
else dp[i] +=0;
}
return dp[n-1];
}上面的代码中，我们的初始化也走了一边填表的逻辑，显得有点冗余，有没有什么方法可以进行优化？
- 另一种 dp 解法，常用来处理边界情况；
可以将dp 多开辟一个空间（添加一个虚拟位置），让原来dp[1] 初始化的逻辑放在调表逻辑中；
要初始化的永远是dp 表中的前两个位置，但是新dp 通过增加一个虚拟结点，就让原本下标为1的变成了下标为2 的，也就是将原本dp[1] 的初始化逻辑合并到了填表逻辑之中；
注意事项：
1、为什么可以保证原本第二个初始化的数据放在新dp 表中的填表逻辑填时是正确的？首先保证新增的虚拟结点中的值保证后面的填表是正确的；
2、注意dp 表与原数组的下标映射关系
Q: 增加了一个虚拟结点之后，dp[0]应该初始化为什么？
- 我们的状态转移方程： dp[i] = dp[s[i] 单独解码] + dp[s[i-1] 与 s[i] 结合后再解码]；当s[0] 可以单独解码，s[1] 可以单独解码并且 s[0] 与 s[1] 还可以结合一起解码的时候，那么dp[2] = dp[0] + dp[1]得要是2，所以dp[0] 要初始化为1；
优化参考代码：
int numDecodings(string s)
{
int n = s.size();
//dp[i]: 以 i 位置结束的解码方案的总数
//状态转移方程需要分情况讨论，4种情况
//初始化：也需要讨论 填表顺序：从左往右 返回值 :dp[n-1]
vector<int> dp(n+1);//增加一个虚拟结点
//初始化
dp[0] = 1;
dp[1] = s[0]== '0' ? 0: 1;//注意下标的映射关系
//边界情况处理
if(n==1) return dp[1];
//填表
for(int i = 2;i<=n;i++)
{
//判断单个是否解码成功
if(s[i-1]!='0') dp[i] = dp[i-1];//注意下标的映射关系
else dp[i] = 0;
//再判断 i-1 与 i 结合解码是否成功
int t = (s[i-2]-'0')*10 + (s[i-1]-'0');//注意下标的映射关系
if(t>=10 && t<=26) dp[i]+=dp[i-2];
else dp[i] +=0;
}
return dp[n];
}总结
动态规划五个步骤：
- 1、确定一个动态表达式
- 2、根据该动态表达式来推导状态转移方程
- 3、初始化
- 4、填表顺序
- 5、返回值
一般有三种方式可以来确定状态表示：
- 1、题目怎么要求，我们就怎么定义状态表示
- 2、经验 + 题目要求
- 3、分析题目的过程中发现重复的子问题（再将重复的子问题抽象为状态表达式）
推导状态转移方程：1、用之前或者之后的状态推导得到dp[i] 的值 2、根据最近的一步来划分问题;
初始化的目的：保证填dp表（根据状态转移方程来调表）的时候不会发生越界；
填表顺序的目的是为了保证在填表的时候，所要依据的状态已经存在了；
扫一扫
2715
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
