5. 金融机器学习之【基于强化学习的量化交易】

目前学界 RL 在量化交易里面的应用大致分为4种：Portfolio Management（投资组合管理），Single-asset trading signal （单资产交易信号），Execution（交易执行）以及Option hedging（期权对冲和定价）。RL的技术发展十分迅速，在此只是入门级别的知识铺垫。笔者注。

阅读难度：★★☆☆☆（本科/高年级水平）

一、预备知识

强化学习（RL）

强化学习是一种（第三种）机器学习范式，研究智能体与环境交互，通过试错学习最大化累积奖励的策略。会在文章中具体阐释其定义、算法和应用。

二、强化学习简介

1、马尔可夫决策过程（MDP）

文章将 RL 定义为一系列最大化智能体与环境（确定性或随机）交互的预期奖励的方法，在量化金融中常对应确定性和随机最优控制问题。

RL 包含基于动态规划原理的最优控制技术，在两方面更具优势：（1）RL 不依赖网格（grid），而采用函数近似，可以减轻维度灾难；（2）RL 利用数据样本，无需已知状态转移核（transition kernel）。

最优控制是从工程角度解读最优化问题，即在可行条件下寻求最佳控制策略，以使控制系统能够最优地到达目标。笔者注。

马尔可夫决策（Markov decision processes，MDP） 是 RL 的核心框架，形式化为三元组：

S 为状态空间（state space），用于描述系统的可能状态，可为有限 / 可数集或有限维空间子集；
A 为动作空间（action space），用于描述智能体（agent）的可选动作，性质同状态空间；
P 为概率核（probability kernel ），将（s, a）映射到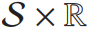上的概率测度，刻画给定状态 s 和动作 a 时，下一状态与对应奖励的分布。

实际中，P 可拆分为状态转移核（给定 s 和 a，下一状态 s' 的分布）和奖励概率分布（给定 s, a, s' 的奖励分布，或简化为期望奖励函数）。

2、基于MDP的优化问题

基于 MDP 的优化问题分两类：

有限 horizon 问题，最大化预期累积奖励与最终收益之和：

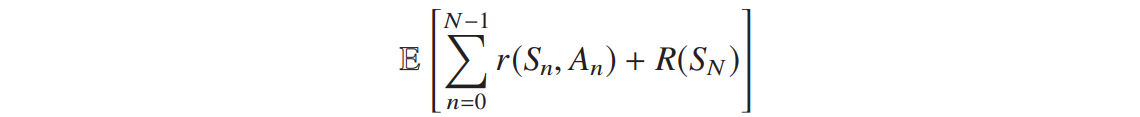
horizon 指的是投资期。笔者注。

无限 horizon 问题，最大化预期折扣累积奖励，其中 γ∈(0,1) 为折扣因子：

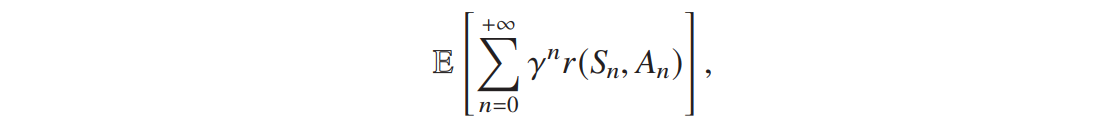
3、核心概念

RL 的核心概念与 MDP 的核心概念高度绑定，主要包括：

策略（Policy）：将时间和状态映射到动作（确定性策略）或动作空间上的概率测度（随机策略），不依赖时间的策略为平稳策略；
最优策略（Optimal policy）：最大化目标函数 / 预期奖励的策略；
价值函数（Value function）：评估策略性能，将状态映射到预期奖励。

价值函数与目标函数的核心区别在于，目标函数是全局优化目标（如最大化总收益），而价值函数是局部评估工具（如在某一状态下遵循特定策略的预期收益）。通过价值函数，强化学习算法可迭代改进策略，逐步逼近最优目标。笔者注。

有限 horizon 下，策略的价值函数为给定时刻 k 和状态 s 时，从 k 到 N-1 的累积奖励与最终收益的条件期望：

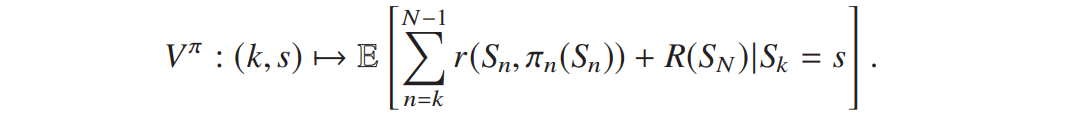
无限 horizon 下，平稳策略的价值函数为从初始状态 s 开始的折扣累积奖励的条件期望：

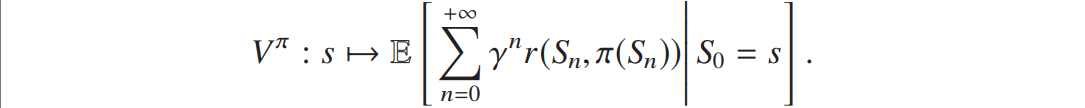
最优价值函数（Optimal value function）：最优策略对应的价值函数；
状态 - 动作价值函数 / Q 函数（State-action value function or Q function）：给定首个动作时的价值函数。

有限 horizon 下，为给定时刻 k、状态 s 和初始动作 a 时的预期奖励：

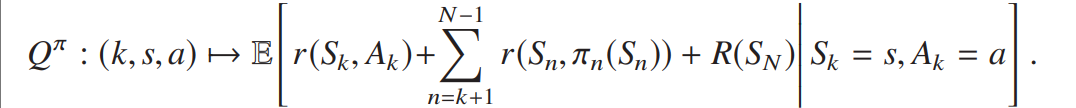
该公式定义了有限 horizon 下策略的价值函数。它表示在第 k 步处于状态 s 时，遵循策略（即从第k步开始，每一步按选择动作）所能获得的总预期收益，具体为从第 k 步到 N-1步的即时奖励之和，加上最终时刻的终端收益，再在已知当前状态 s 的条件下取期望。价值函数是强化学习中评估策略优劣的核心工具，例如在算法交易中，可用于衡量某一执行策略在特定时刻和市场状态下的潜在收益。笔者注。

无限 horizon 下，为对应场景的预期折扣奖励：

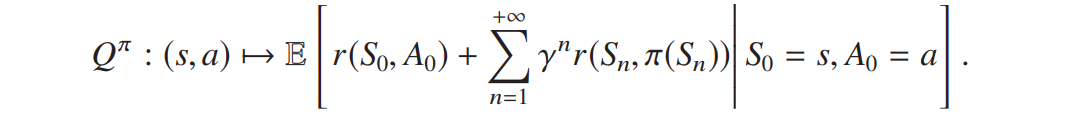
最优 Q 函数（Optimal state-action value function or optimal Q function）：最优策略对应的 Q 函数；
贪婪策略（Greedy policy）：基于价值函数选择最大化即时奖励与未来预期奖励之和的动作，在有限 horizon 下，

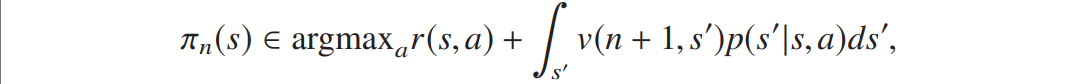
在无限 horizon 下，

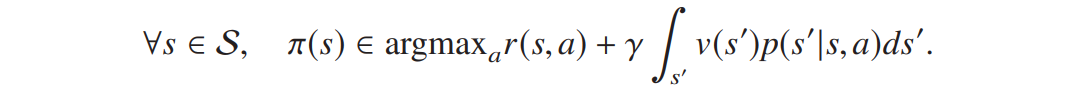
需要明确：对最优价值函数贪婪的策略即为最优策略。

在金融中，价值函数的学习难度极高：市场非平稳（转移概率随时间变化）、状态空间高维（需纳入多变量），因此实际应用中常通过近似动态规划（如神经网络拟合 v）和模拟数据训练（替代真实市场的转移概率）来实现。笔者注。

4、主要 RL 方法介绍

4.1 无限 horizon 问题

无限 horizon 问题的核心是贝尔曼方程（价值函数的不动点方程）。

一般策略的价值函数满足线性贝尔曼方程：

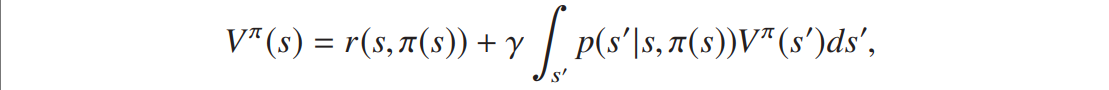
写成线性算子的形式有：。

线性算子是指从一个向量空间到其自身的线性变换。笔者注。

最优价值函数满足非线性贝尔曼方程：

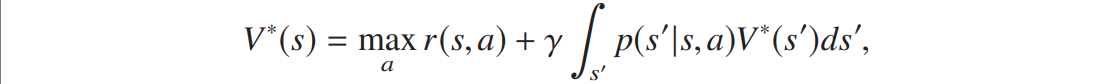
写成非线性算子的形式有：。

为了得到最有价值函数，求解非线性贝尔曼方程有两种路径：

第一种是价值函数迭代法，通过的迭代逼近最优价值函数，虽然收敛，但在状态 / 动作空间过大时不可行，需用近似动态规划（如神经网络参数化价值函数）。

第二种是策略迭代法，通过交替进行策略评估（计算当前策略的价值函数，可用蒙特卡洛、时序差分（TD）学习等）和策略改进（基于当前价值函数更新为贪婪策略）。

策略迭代法需要已知转移核。笔者注。

TD 学习是关键技术，能够实现无需了解底层模型（主要是转移核）的学习过程。通过数据样本更新价值函数近似，如利用序列，沿方向调整。

除了单纯地使用价值函数，许多强化学习方法基于参数化策略（例如，使用神经网络）找到最优。和价值函数类似，通过更新策略参数进行优化，在有限horizon问题中常用。笔者注。

基于 Q 函数的 TD 学习衍生出 SARSA 和 Q-learning 算法，可直接逼近最优 Q 函数，在游戏中应用广泛。

SARSA 因 “在线” 特性适合需实时适应的简单游戏（如迷宫、悬崖的行走），Q-learning 因 “离线最优” 特性适合需全局规划的复杂游戏（围棋）。笔者注。

4.2 有限 horizon 问题

价值函数同样满足贝尔曼方程，形式有相对应的变化

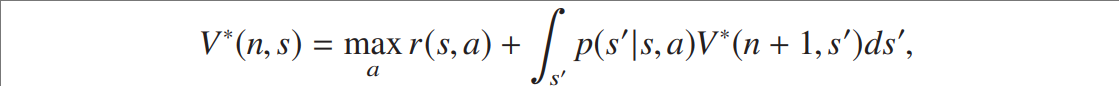
以最优价值函数为例。笔者注。

有三种思路：

策略迭代法可适配（将时间纳入状态）。

近似动态规划需逆向时序近似价值函数，但存在采样点选择难题。

这两种方法和无限 horizon 问题是类似的。笔者注。

最后，前文提到，直接策略搜索不依赖价值函数，将策略参数化（如神经网络系数），通过随机优化最大化预期奖励，但易受梯度消失 / 爆炸影响，可通过逆向归纳缓解（先近似后期最优决策，再冻结以近似前期）。

TD 学习是 RL 的核心创新之一，其 “时序差分” 指利用相邻时间步的价值估计差异更新模型，无需等待完整轨迹结束（如蒙特卡洛方法），适合在线学习。而直接策略搜索跳过价值函数估计，直接优化策略参数，在高维度动作空间中更灵活，但需解决梯度不稳定问题。笔者注。

三、金融场景

文章强调，金融问题与 RL 成功应用的游戏 / 玩具问题有本质区别，需理性看待 RL 在金融中的应用。文章讨论了 RL 在金融场景应用面临的挑战：状态与动作空间、模型的作用、风险考量、时间步问题。在此不一一展开。

实际上，RL 在金融领域中能够解决的问题是比较局限的，在业务中也并不常用。笔者注。

四、现有研究回顾

文章这部分类似文献综述，我不在此列举。考虑到这些金融场景下的实践在 RL 框架外也是可以实现的，因此我会按照：[原有模式]-[RL在其中的作用]的逻辑进行讲述。笔者注。

1、统计套利

统计套利的核心是寻找资产价格的统计规律（如均值回归、协整关系）并设计交易策略，传统上可通过回归分析、时间序列模型（如 ARIMA）、因子模型等实现。

例如，通过检验资产价差的平稳性构建配对交易策略，无需依赖 RL。

但 RL 对统计套利的提升体现在两方面：

1.1 动态环境的适应性

金融市场规律具有时变性（如套利空间随市场情绪变化），RL 通过持续与环境交互（试错学习），可动态调整策略（如持仓比例、止损阈值），而传统静态模型需手动更新参数。

文章中 Moody 等人（2001）的研究显示，RL 策略能通过梯度优化实时调整风险调整指标（如夏普比率），适应市场波动。

与神经网络的反向传播效果类似。笔者注。

1.2 端到端优化

传统方法需分步骤完成： “特征提取→规律建模→策略生成”，而 RL 可直接从原始数据（如高频价格、成交量）中学习 “状态→动作” 映射（如通过神经网络输出持仓），减少手动特征工程的偏差。

例如，Carapuço 等人（2018）用 DQN 处理市场微观结构数据，直接输出交易决策，避免了人为筛选特征的局限性。

2、最优执行

最优执行的核心是拆分大额订单以平衡市场冲击与时间风险，传统方法以 Almgren-Chriss 模型（传送门）为代表，基于明确的市场冲击假设（如线性冲击函数）和动态规划求解，在假设成立的简单场景下可高效应用。

RL 对最优执行的提升集中在突破模型假设限制：

2.1 无需预设市场冲击模型

传统模型依赖对市场冲击（如订单对价格的影响）的参数化假设，而实际冲击受流动性、订单簿深度等多因素影响，难以精确建模。

RL 可通过模拟数据或历史数据直接学习冲击规律，例如 Ning 等人（2018）用双 DQN 处理 1 秒级高频数据，无需预设冲击函数，仅通过状态（剩余库存、波动率）学习最优下单量。

2.2 处理高维度状态

当执行涉及多资产、多市场（如跨交易所路由）时，传统模型因维度灾难难以扩展，而 RL 通过函数近似（如神经网络）可高效处理高维度状态（如多资产价差、各市场流动性）。

文章中 Karpe 等人（2020）的双 DQN 模型纳入买卖价差、市场失衡等多维度特征，优化限价单 / 市价单选择，优于传统单因素模型。

2.3 动态调整策略

这个思路跟 1.1 是接近的，这里指路一篇2014年在 AAAI 上的一篇论文。（传送门）

3、做市策略

做市策略的核心是设置买卖报价以平衡库存风险与盈利，传统方法以 Avellaneda-Stoikov 模型（传送门）为代表，基于随机最优控制，假设价格动态与库存演化符合特定随机过程（如布朗运动），在简化场景下可求解解析解。

RL 对做市策略的提升体现在复杂目标与交互的建模能力：

3.1 多目标动态平衡

做市商需同时优化价差收入、库存成本、流动性风险等，传统模型常简化目标函数（如仅考虑库存平方惩罚），而 RL 可通过奖励函数设计（如结合价差收益与库存波动率惩罚）直接平衡多目标。

这个在 4.1 就简单介绍过了。笔者注。

例如，Spooner 等人（2018）用 SARSA 算法处理限价订单簿数据，奖励函数同时纳入成交收益与库存风险，实现更贴近实际的做市决策。

3.2 模拟多主体交互

实际市场中做市商需应对其他交易者（如知情者、流动性交易者）的策略性行为，传统模型难以刻画这种动态交互。RL 可通过多智能体模拟（如文中提及的 Ganesh 等人（2019）的多做市商模拟市场），学习在竞争环境中调整报价，提升策略鲁棒性。

五、展望

文章指出，现有研究多为概念验证，未来金融机构需构建可扩展的 RL 执行和做市算法。作者强调，近期 RL 突破主要是技术整合（而非科学创新），如 AlphaZero 的成功源于 “已知思想的巧妙实现与强大计算能力”。

因此，传统量化分析师、计算机科学家和工程师的合作是 RL 交易智能体大规模应用的必要条件。

总结

本篇文章为文献综述和学科发展回顾的论文，涉及到了专业术语解释、数理模型构建、技术发展回顾等。适合已有金融市场、机器学习基础知识的学生及从业者进行阅读学习。

更多的文章请关注该文章解读系列，我会持续更新。

欢迎各位读者在评论区交流讨论。