acwing刷题指南7

原创

已于 2022-07-19 00:42:19 修改 · 864 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构

于 2022-05-24 22:19:50 首次发布

//数据结构篇

好像单链表和双链表没写到上面来，不过没事，后面图论再写

题目列表：

828. 模拟栈

829. 模拟队列

830. 单调栈（找在右边比自己小的数，构成单调递增区间（反之））

154. 滑动窗口（类似于单调栈不过又像极了双端队列）

P1614 爱与愁的心痛

都可以画图解释

836. 合并集合（并查集）

837. 连通块中点的数量

学习笔记：

for(int i = 0; i < 8; i ++) p[i] = i;//初始化

得到下图

很容易理解，就是将当前数据的父节点指向自己

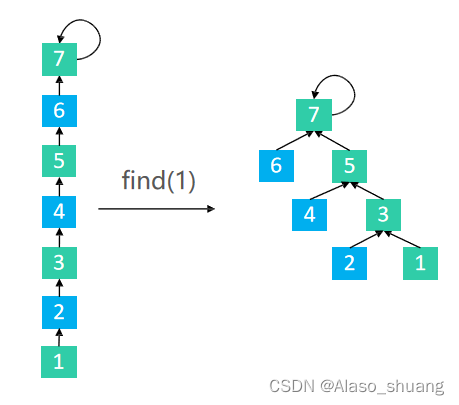
查找 + 路径压缩

find(1) p[1] = 2 p[1] = find(2)
find(2) p[2] = 3 p[2] = find(3)
find(3) p[3] = 4 p[3] = find(4)
find(4) p[4] = 4 将p[4]返回

退到上一层
find(3) p[3] = 4 p[3] = 4 将p[3]返回
退到上一层
find(2) p[2] = 3 p[2] = 4 将p[2]返回
退到上一层
find(1) p[1] = 2 p[1] = 4 将p[1]返回

至此，我们发现所有的1，2，3的父节点全部置为了4，实现路径压缩；同时也实现了1的父节点的返回

合并操作
if(op[0] == ‘M’) fa[find(a)] = find(b); //将a的祖先点的父节点置为b的祖先节点

其他路径压缩方法

1.路径分裂：使路径上的每个节点都指向其祖父节点（parent的parent）(这是我们这题836. 合并集合所选择用的)

2 路径减半：使路径上每隔一个节点就指向其祖父节点（parent的parent）

int find(int x){
while(x != fa[x]){
fa[x] = fa[fa[x]];
x = fa[x];
}
return x;
}

总结
并查集
1.将两个集合合并
2.询问两个元素是否在一个集合中

基本原理：每个集合用一棵树来表示。树的编号就是整个集合的编号。每个节点存储它的父节点，fa[x]表示x的父节点

1.判断树根 if(fa[x] = x)
2.求x的集合编号 while(fa[x] != x) x = fa[x]
3.合并两个集合，这两将x的根节点嫁接到y的根节点, px为x的根节点， py为y的根节点，嫁接p[px] = py

字符串算法：

831. KMP字符串(KMP主要分两步：求next数组、匹配字符串)

835. Trie字符串统计

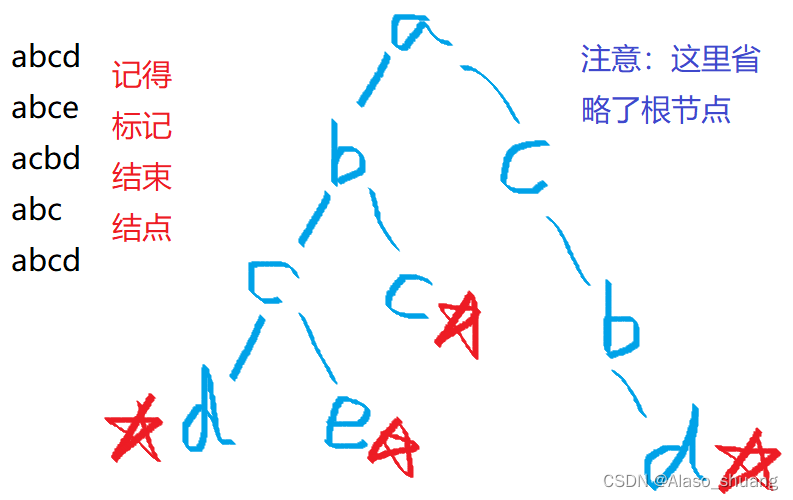
Trie树(是一种能够高效存储和查找字符串集合的数据结构)

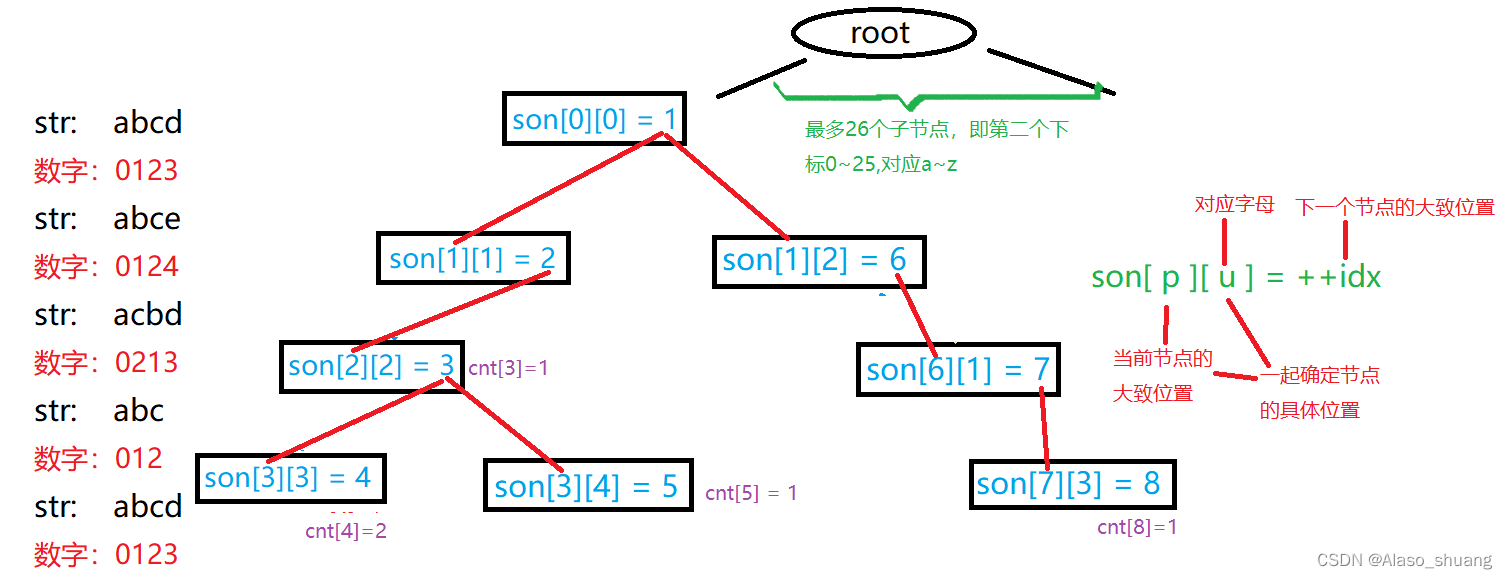
Trie树中有个二维数组 son[N][26]，表示当前结点的儿子，如果没有的话，可以等于++idx。

Trie树本质上是一颗多叉树，对于字母而言最多有26个子结点。所以这个数组包含了两条信息。比如：son[1][0]=2表示1结点的一个值为a的子结点为结点2;如果son[1][0] = 0，则意味着没有值为a子结点。这里的son[N][26]相当于链表中的ne[N]。

堆：

838. 堆排序

hash:

840. 模拟散列表

828. 模拟栈

模板题

有手就行

#include<iostream>
using namespace std;
const int N = 100010;
int stk[N],tt;
int m;
void push(int x)
{
tt++;
stk[tt] = x;
}
void pop()
{
tt--;
}
void empty()
{
if(tt)cout<<"NO"<<endl;
else cout<<"YES"<<endl;
}
int query()
{
return stk[tt];
}

int main()
{
cin>>m;
while(m--)
{
string op;
cin>>op;
if(op == "push")
{
int x;
cin>>x;
push(x);
}
else if(op == "pop")pop();
else if(op == "empty")empty();
else cout<<query()<<endl;
}
return 0;
}