TensorFlow学习笔记（二）

TensorFlow深度学习实践：激活函数与损失函数

最新推荐文章于 2025-12-10 20:48:21 发布

原创最新推荐文章于 2025-12-10 20:48:21 发布 · 492 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#神经网络 #tensorflow #深度学习 #python

TensorFlow 专栏收录该内容

7 篇文章

订阅专栏

这篇博客探讨了在TensorFlow中进行深度学习时的关键概念，包括各种激活函数如relu、sigmoid和tanh，以及常见的损失函数如均方误差和交叉熵。此外，还讨论了学习率的选择、滑动平均技术的应用以及正则化策略，通过实例进一步巩固这些知识点。

部署运行你感兴趣的模型镜像

文章目录

激活函数

常用的激活函数有：relu、sigmoid、tanh等。
在这里插入图片描述

损失函数

在这里插入图片描述
常用的损失函数有均方误差、自定义、交叉熵等。

学习率

在这里插入图片描述

滑动平均

在这里插入图片描述

正则化

在这里插入图片描述

例题

在这里插入图片描述

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
BATCH_SIZE=30
seed=2

rdm=np.random.RandomState(seed)
X=rdm.randn(300,2)
Y_=[int(x0*x0+x1*x1<2)for (x0,x1) in X]
Y_c=[['red' if y else 'blue'] for y in Y_]
X=np.vstack(X).reshape(-1,2)
Y_=np.vstack(Y_).reshape(-1,1)
print(X)
print(Y_)
print(Y_c)
plt.scatter(X[:,0],X[:,1],c=np.squeeze(Y_c))

# 定义神经网络的输入、参数和输出，定义前向传播过程
def get_weight(shape,regularizer):
    w=tf.Variable(tf.random_normal(shape),dtype=tf.float32)
    tf.add_to_collection('losses',tf.contrib.layers.l2_regularizer(regularizer)(w))
    return w
def get_bias(shape):
    b=tf.Variable(tf.constant(0.01,shape=shape))
    return b
x=tf.placeholder(tf.float32,shape=(None,2))
y_=tf.placeholder(tf.float32,shape=(None,1))
w1=get_weight([2,11],0.01)
b1=get_bias([11])
y1=tf.nn.relu(tf.matmul(x,w1)+b1)

w2=get_weight([11,1],0.01)
b2=get_bias([1])
y=tf.matmul(y1,w2)+b2

loss_mse=tf.reduce_mean(tf.square(y-y_))
loss_total=loss_mse+tf.add_n(tf.get_collection('losses'))

# 定义反向传播的方法，不含正则化
train_step=tf.train.AdamOptimizer(0.0001).minimize(loss_mse)

with tf.Session() as sess:
    init_op=tf.global_variables_initializer()
    sess.run(init_op)
    STEPS=40000
    for i in range(STEPS):
        start=(i*BATCH_SIZE)%300
        end=start+BATCH_SIZE
        sess.run(train_step,feed_dict={x:X[start:end],y_:Y_[start:end]})
        if i%2000==0:
            loss_mse_v=sess.run(loss_mse,feed_dict={x:X,y_:Y_})
            print("After %d steps, loss is %f"%(i,loss_mse_v))
    xx, yy = np.mgrid[-3:3:.01, -3:3:.01]
    grid=np.c_[xx.ravel(),yy.ravel()]
    probs=sess.run(y,feed_dict={x:grid})
    probs=probs.reshape(xx.shape)
    print("w1: \n",sess.run(w1))
    print("b1: \n",sess.run(b1))
    print("w2: \n",sess.run(w2))

plt.scatter(X[:,0],X[:,1],c=np.squeeze(Y_c))
plt.contour(xx,yy,probs,levels=[.5])

After 0 steps, loss is 4.818219
After 2000 steps, loss is 1.114521
After 4000 steps, loss is 0.440926
After 6000 steps, loss is 0.199151
After 8000 steps, loss is 0.131880
After 10000 steps, loss is 0.100423
After 12000 steps, loss is 0.082595
After 14000 steps, loss is 0.075924
After 16000 steps, loss is 0.072781
After 18000 steps, loss is 0.071144
After 20000 steps, loss is 0.070309
After 22000 steps, loss is 0.069843
After 24000 steps, loss is 0.069528
After 26000 steps, loss is 0.069235
After 28000 steps, loss is 0.068985
After 30000 steps, loss is 0.068852
After 32000 steps, loss is 0.068761
After 34000 steps, loss is 0.068719
After 36000 steps, loss is 0.068692
After 38000 steps, loss is 0.068671
w1: 
 [[ 0.45716277 -0.7401704  -0.20684825  0.32292303 -0.68535405  0.7540642
   0.69503736 -0.38029185  1.0381353  -0.07026183 -1.5209175 ]
 [-1.2057172   0.8689282   0.9055338  -0.06462611  1.9524144   0.8229273
   1.3031511   0.77961135  0.85217774  0.95951426  1.7135825 ]]
b1: 
 [-0.7522732  -0.14688005  0.1519486   0.5435965   0.04393205  0.00962955
  0.14700696  0.06079181  0.08799052  0.22217858 -0.00777696]
w2: 
 [[-0.7839962 ]
 [-0.9626764 ]
 [-0.86231494]
 [ 1.1390938 ]
 [-0.3122795 ]
 [ 0.8863838 ]
 [-0.5035166 ]
 [ 1.3335979 ]
 [-0.98545325]
 [ 1.3350753 ]
 [ 0.07136385]]

在这里插入图片描述

# 定义反向传播方法，包含正则化
train_step = tf.train.AdamOptimizer(0.0001).minimize(loss_total)

with tf.Session() as sess:
    init_op=tf.global_variables_initializer()
    sess.run(init_op)
    STEPS=40000
    for i in range(STEPS):
        start=(i*BATCH_SIZE)%300
        end=start+BATCH_SIZE
        sess.run(train_step, feed_dict={x:X[start:end],y_:Y_[start:end]})
        if i%2000==0:
            loss_v=sess.run(loss_total,feed_dict={x:X,y_:Y_})
            print("After %d steps, loss is: %f"%(i,loss_v))
    xx, yy = np.mgrid[-3:3:0.01, -3:3:0.01]
    grid=np.c_[xx.ravel(),yy.ravel()]
    probs=sess.run(y,feed_dict={x:grid})
    probs=probs.reshape(xx.shape)
    print("w1:\n",sess.run(w1))
    print("b1:\n",sess.run(b1))
    print("w2:\n",sess.run(w2))
    print("b2:\n",sess.run(b2))
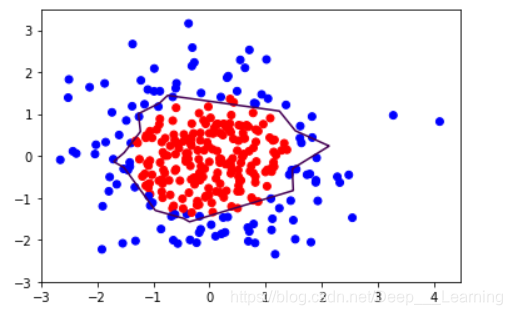
plt.scatter(X[:,0],X[:,1],c=np.squeeze(Y_c))
plt.contour(xx,yy,probs,levels=[.5])

After 0 steps, loss is: 11.275545
After 2000 steps, loss is: 1.232818
After 4000 steps, loss is: 0.465125
After 6000 steps, loss is: 0.380577
After 8000 steps, loss is: 0.320099
After 10000 steps, loss is: 0.272106
After 12000 steps, loss is: 0.238350
After 14000 steps, loss is: 0.213717
After 16000 steps, loss is: 0.195418
After 18000 steps, loss is: 0.181378
After 20000 steps, loss is: 0.171185
After 22000 steps, loss is: 0.163568
After 24000 steps, loss is: 0.156573
After 26000 steps, loss is: 0.150386
After 28000 steps, loss is: 0.145822
After 30000 steps, loss is: 0.141759
After 32000 steps, loss is: 0.138124
After 34000 steps, loss is: 0.134294
After 36000 steps, loss is: 0.131309
After 38000 steps, loss is: 0.128560
w1:
 [[ 0.42574826 -0.11000597 -0.28807208 -0.8295783  -0.08520512  0.15115976
   0.49556816  0.14580503  0.2802947   0.51000607  0.04589701]
 [-0.39741394 -0.3030124  -0.8894444  -0.10718283 -0.20497411 -1.5591075
   0.7474861  -0.5083292  -0.04024008  0.07837258  0.32959813]]
b1:
 [-0.10522619  0.5297696   0.16505523 -0.46243635  0.3803159   0.04817935
 -0.12547617  0.08252801  0.49434888  0.35443753  0.0433147 ]
w2:
 [[-0.783308  ]
 [ 0.4830831 ]
 [ 0.46736714]
 [-0.87343204]
 [ 0.19101967]
 [-0.7334284 ]
 [-0.7889217 ]
 [ 0.62166184]
 [ 0.2399536 ]
 [ 0.5128802 ]
 [ 0.5036762 ]]
b2:
 [0.506138]