正题
基本算法
最大流算法:DinicDinicDinic
费用流算法:EK+SPFAEK+SPFAEK+SPFA
可行流定义:
容量限制:所有边的流量不高于上界,不低于下界
流量平衡:除源汇外,所有点入流量 === 出流量
时间复杂度
DinicDinicDinic:每次 bfsbfsbfs 分层,dfsdfsdfs 找增广路,暴力加,当前弧优化,时间复杂度 O(n2m)O(n^2m)O(n2m) 。
DinicDinicDinic的时间复杂度很玄学,在大部分情况下都远远好于上面这一个复杂度,下面是两个例子:
1.如果容量只有 111 ,时间复杂度不超过 O(min(n23,m12)m)O(\min(n^{\frac{2}{3}},m^{\frac{1}{2}})m)O(min(n32,m21)m) 。
2.如果除源汇之外每个点入度只有一条且容量为 111 或出度只有一条且容量为 111,时间复杂度不超过 O(nm)O(\sqrt{n}m)O(nm) ,如二分图匹配。
最小费用最大流(EK):O(SPFA(n,m)∗f)O(SPFA(n,m)*f)O(SPFA(n,m)∗f),其中 fff 是流量。
最大流最小割定理
不作深入研究。
如何找最小割的方案?从 SSS 开始在残余网络上 dfsdfsdfs ,能 dfsdfsdfs 到的点就是属于 SSS 集的,否则就是属于 TTT 集的,如果一条边将 SSS 到 TTT 连起来了,那么这条边就叫做割边。那么这组割恰好等于最大流,所以这组割就是一组最小割。
各类问题的解法路径汇总
有上下界的可行流:强设流量满足下界 →\to→ 求附加图满流得到原图可行流
有上下界的最大流:求出有上下界的可行流 →\to→ 求源到汇的最大流
有上下界的最小流:求出有上下界的可行流 →\to→ 求汇到源的最大流
任何最大费用流问题:边权取相反数转化为对应最小费用流问题
一般的最小费用可行流:最短路增广直到费用非负
一般的最小费用最大流:最短路增广直到找不到增广路
有上下界、带负边的最小费用可行流:非负边流量设为下界,负边流量设为上界 →\to→ 求附加图最小费用满流得到原图最小费用可行流
有上下界、带负边的最小费用最大流:求出最小费用可行流→求源到汇的最小费用最大流
无源汇指定点或边最大/小流↔有源汇最大/小流
常用建图技巧
拆点:限点容、改变费用、划分阶段
限定边满流:流量必须为定值的边等于上下界相等
重复边合并:两个点之间的多条边容量合并
分拆重复边:不同次经过时产生的费用/收益不同
单入边或出边省点:一个点只有一条入边时可能去掉该点
定流边转化:一条边上下界相等时往往能够转化或删去
平凡可行流简化:如果可行流有简单解,可以省掉在附加图上跑算法的步骤
整数流量原理
如果边的容量都是整数,那么:
1.最大流的数值是整数。
2.存在至少一个最大流的流量网络,每条边流量都是整数。
3.用常见的几个最大流算法,求出的流量网络每条边流量都是整数。
推论:
1.如果容量都是 xxx 的倍数,那么上述各处“整数”都可以替换成“x的倍数”。
2.如果容量在实数意义下的最大公约数是 xxx ,那么上述各处“整数”都可以替换成“x的倍数”。
网络流的优化
1.建图中冗余边、点的合并
2.数据结构辅助冗余合并
3.数据结构优化增广
4.动态建图
s-t最小割简介
割:有向图中给定点 xxx 和 yyy ,去掉一些边使得不存在 xxx 通往 yyy 的路径。
最小割:带权有向图中边权和最小的割。
解法:
1.最大流=最小割
2.边权视为容量,点 x 和 y 分别视为源点和汇点
3.新图的最大流等于原图的最小割
4.最小割模型里面没有容量、流量的概念
在实际问题中,最小割和最大流的模型完全不同,不要混淆。
最小割的常见特点是“划分为两类或更多类”。
一些例题
T1

对于每个小朋友建一个点:
最小割建图。 本来是同意的,(S,i,o)(S,i,o)(S,i,o) ,(i,T,o+1)(i,T,o+1)(i,T,o+1) 。
本来是反对的,(S,i,o+1)(S,i,o+1)(S,i,o+1),(i,T,o)(i,T,o)(i,T,o) 。 好朋友 (a,b,1)(a,b,1)(a,b,1)。
ooo 取一个较大的数,是为了保证不两边都割,割两边分别表示同意/不同意,如果割的不同侧就需要多割中间好朋友那条。
因为如果割的是不同侧,两个小朋友之间的连边和这两个小朋友未被割掉的边形成了一个路径,联通了 SSS 和 TTT ,所以要用 111 的代价来割断它,也就产生了 111 的冲突。
T2
有 nnn 门课程和 mmm 个学期。 有一些课程有先修课程,输入 kkk 个限制,形如 a[i]a[i]a[i] 是 b[i]b[i]b[i] 的先修课程。 每一门课程在每个学期可能获得不同的绩点。 你需要修完所有课,并输出可以获得的最大绩点,你的绩点就是每门课的绩点的平均值。
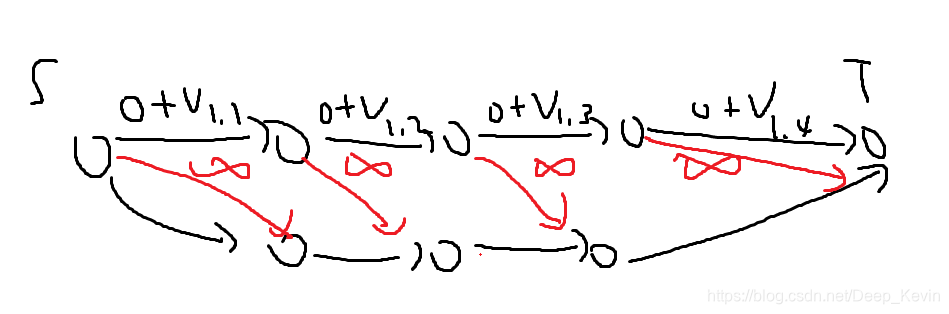
类似这样建图,若在 a[i]a[i]a[i] 的第 xxx 次割断, b[i]b[i]b[i] 的第 yyy 次割断 (y<=x)(y<=x)(y<=x) ,那么就会产生一条 SSS到 TTT 的通路,需要割掉 inf\infinf,矛盾。另外当有环时无解,因为这时相当于有一条从 SSS 到 TTT 的正无穷通路。
T3
n∗mn*mn∗m 的棋盘,有些格子有棋子。 每次可以拿走同行或同列若干连续棋子,求至少需要多少次操作可以拿走所有棋子。
考虑将棋子建点, SSS 连向一个棋子,容量为 ooo 表示棋子在列被拿掉,一个棋子连向 TTT 表示棋子在行被拿掉。然后相邻的棋子直接考虑文理分科模型。
LG P4313
文理分科是一件很纠结的事情!小 PPP 所在的班级要进行文理分科。他的班级可以用一个 n∗mn*mn∗m 的矩阵进行描述,每个格子代表一个同学的座位。
每位同学必须从文科和理科中选择一科。同学们在选择科目的时候会获得一个满意值。
满意值按如下的方式得到:
1.如果第 iii 行第 jjj 列的同学选择了文科,则他将获得 art[i][j]art[i][j]art[i][j] 的满意值,如果选择理科,将得到 science[i][j]science[i][j]science[i][j] 的满意值。
2.如果第 iii 行第 jjj 列的同学选择了文科,并且他相邻(两个格子相邻当且仅当它们拥有一条相同的边)的同学全部选择了文科,则他会更开心,所以会增加 sameart[i][j]same_art[i][j]sameart[i][j] 的满意值。
3.如果第 iii 行第 jjj 列的同学选择了理科,并且他相邻的同学全部选择了理科,则增加 samescience[i][j]same_science[i][j]samescience[i][j] 的满意值。 小 PPP 想知道,大家应该如何选择,才能使所有人的满意值之和最大。请告诉他这个最大值。
这题对于每一个同学建一个点, SSS 向每个同学连容量为 sciscisci 的边表示选文,每个同学向汇点连一条容量为 artartart 的边表示选理,对于每个自己与周围的同学,连向一个新建的点,流量为正无穷,这个点向汇点连一条这些同学同时选文的收益。 然后用全部的值减去最小割就可以。
证明考虑,若有一个不选文就会产生一条从S到T的路径,要把收益割掉,否则就要将选文的代价割掉,显然正确。上述建边与证明理科同理。
Topcoder SRM 558
n∗mn*mn∗m 的棋盘,每个点有选择代价和控制收益。 一个点被控制当且仅当它被选择或者它的邻居都被选择。
考虑黑白染色,要么就是自己被选,要么就是自己不被选且周围四个被选,连向黑点的边和连向白点的边反一下就可以套文理分科模型。
POJ 1637 混合图欧拉回路
给出 n(≤200)n(\leq 200)n(≤200) 个点,m(≤1000)m(\leq 1000)m(≤1000)条边的“混合图”:即有的边规定了方向,有的边没有规定方向。
每条边只能经过一次,问是否存在欧拉回路。
我们设 degi=ini−outideg_i=in_i-out_idegi=ini−outi ,先给所有的无向边定一个方向:(u,v)(u,v)(u,v) ,容易知道,改变一条无向边的方向,只会给两端的 deg±2deg\pm 2deg±2 ,由于一条欧拉回路我们要求所有点的 deg=0deg=0deg=0 。
所以很容易知道如果初始的 degdegdeg有奇数那么就无解,否则我们从 SSS 向 deg<0deg<0deg<0 的 点连一条容量为 −deg2-\frac {deg} 2−2deg的边,原图的无向边 (u,v)(u,v)(u,v),现在网络流的图中 (u,v)(u,v)(u,v)连一条容量为 111 的边,deg>0deg>0deg>0 的点向 TTT 连一条容量为 deg2\frac {deg} 22deg 的边。
当满流的时候即为有解,欧拉路同理。
NOI 2008 志愿者招募
总共 n(≤1000)n(\leq 1000)n(≤1000) 天,第 iii 天需要至少 aia_iai 人工作。
有 m(≤10000)m(\leq 10000)m(≤10000) 类志愿者:第 iii 类可以从第 xix_ixi 天工作到第 yiy_iyi 天,招募费用是每人 cic_ici 元
问满足每天的要求的最少费用和。
网上很多解法都是说拆不等式,这样显得很不优美,考虑一个很好理解的网络流模型。
首先拆点,每个点的下界是 aia_iai ,上界 inf\infinf。连续工作的我们直接从 iii 向 i+1i+1i+1 连边,对于第 jjj 类志愿者从 yjy_jyj 向 xjx_jxj 连边。
然后直接上最小费用可行流,考虑正确性,对于只有一种志愿者的时候,它贡献的必定是所在的循环流,多中志愿者自然就很显然了。
可以考虑构造一种无解的情况,然后看一下跑循环流亦是无解的。可以用单入边来省点优化。
相关的例题有很多,可以去博主的 blogblogblog 里面看看。
CSP 201812 管道清洁
n(≤200)n(\leq 200)n(≤200) 个节点 m(≤500)m (\leq 500)m(≤500) 条边的有向图,需要从 111 号点出发回到 111 号点。
边(管道)有四种:
AAA 类:管道需要被清理,而且可以重复经过
BBB 类:管道需要被清理,但是不能重复经过
CCC 类:管道不需要被清理,而且可以重复经过
DDD 类:管道不需要被清理,但是不能重复经过
需要清理的管道经过一次就视为已经清理
保证:AAA 类和 BBB 类管道构成的子图是弱连通的
保证:111 号点在这个弱连通子图中
问:是否有解,如果有解求完成清理的最短总路程。
可以考虑每种边可以经过的次数就是上界,是否必须经过就是下界,所以这就是一个最小费用可行流。





















 1238
1238

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








