Transformer - layer norm

最新推荐文章于 2025-11-11 02:02:39 发布
原创 最新推荐文章于 2025-11-11 02:02:39 发布 · 390 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文探讨了层归一化（Layer Normalization）在循环神经网络（RNN）中的作用及其与批量归一化（Batch Normalization）的区别。层归一化通过依赖当前时间步中输入到层的总和进行归一化，并在整个时间步骤中共享一组增益（g）和偏置（b）参数。此外，还讨论了协变量偏移的概念及其在机器学习实践中的重要性。
部署运行你感兴趣的模型镜像
  1. Encoder structure

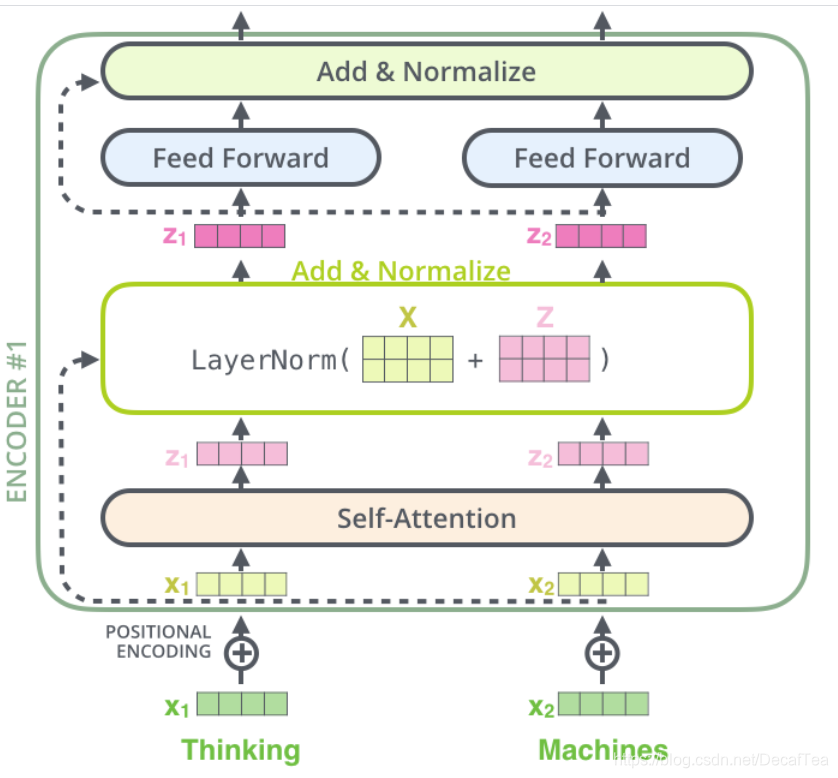
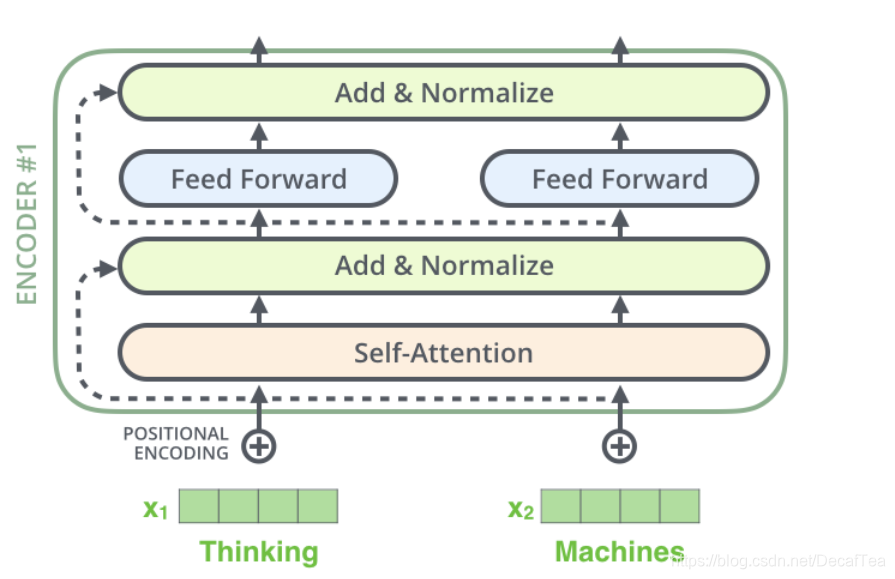
在这里插入图片描述
在这里插入图片描述
2. layer normalization:

  • 什么是covariate shift？
    Covariate shift is the change in the distribution of the covariates specifically, that is, the independent variables.
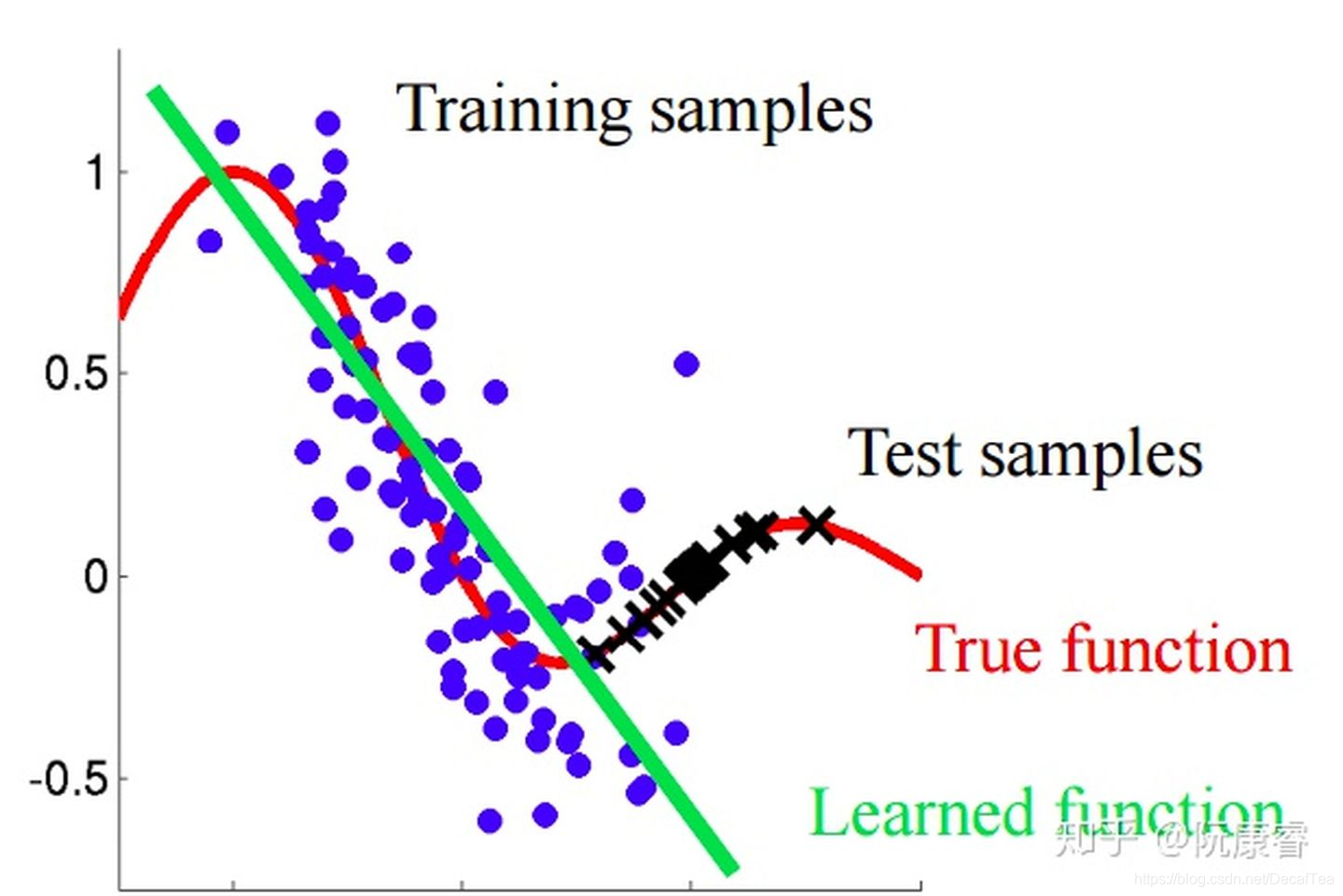
    在这里插入图片描述
    在这里插入图片描述
    在机器学习实践中，我们一定要注意训练数据集和实际情况产生的数据分布不同而带来的影响。

  • batch norm vs layer norm

BN:
在这里插入图片描述
LN:
在这里插入图片描述

  • Layer normalized recurrent neural networks

在这里插入图片描述
its normalization terms dependonly on the summed inputs to a layer at the current time-step. It also has only one set of gain (g) and bias (b) parameters shared over all time-steps.

您可能感兴趣的与本文相关的镜像

Seed-Coder-8B-Base

Seed-Coder-8B-Base

文本生成
Seed-Coder

Seed-Coder是一个功能强大、透明、参数高效的 8B 级开源代码模型系列，包括基础变体、指导变体和推理变体，由字节团队开源

layernorm
数字人生
05-09 1153
LayerNorm最初由Ba等人于2016年提出，并被Vaswani等人在其著名的《Attention is All You Need》论文中引入到Transformer模型中。GPT-2采用了相同的架构，但将LayerNorm的位置移动到了现在被称为预归一化版本的位置，即在Transformer的每个块的第一层进行归一化，这有助于提高训练稳定性。
大模型面试题-为什么transformer块使用LayerNorm而不是BatchNorm
强化学习曾小健
04-04 2560
这意味着,不仅自变量 X 的分布要相同,协变量的分布也应该相同。但是,如果训练数据和测试数据的协变量分布不同,就会出现协变量偏移。所以,协变量偏移强调的是除了主要自变量 X 以外的其他影响因素(即协变量)的分布变化。它提醒我们,在训练和应用机器学习模型时,不能只关注主要自变量,还需要考虑其他相关因素的分布是否一致。NLP任务中经常需要对单个样本做推理,而BatchNorm在推理阶段使用的是训练集的均值和方差,和单个样本的分布可能有偏差。的影响,但是除了 X 以外,还有其他变量也会影响 Y。
【深度学习基础】Vision Transformer 中的 Layer Norm
wangh09的博客
02-15 1659
Layer Norm 是 NLP 常用的归一化层，在ViT中被引入到CV领域。本文对Layer Norm和CV中常用的Batch Norm进行对比来展示这两种运算的相同与不同之处。
深度学习中的层归一化：Transformer架构中的LayerNorm类详解
最新发布
gitblog_00647的博客
11-11 537
还在为深度学习模型训练不稳定而烦恼？Transformer架构中的LayerNorm（层归一化）技术正是解决这一痛点的关键！本文将为你详细解析LayerNorm的工作原理、实现细节及其在Transformer中的重要作用。 读完本文你将获得： - LayerNorm的核心原理和数学公式 - 在Transformer中的具体实现代码 - 与传统BatchNorm的区别和优势 - 实际应用场景和最佳
【笔记】Transformer中的LayerNorm是对某一样本的某一个patch下的所有维度进行正则化：而传统的LayerNorm是对一个batch中的某一个样本的所有channels进行正则化
nyist_yangguang的博客
08-02 372
【代码】【笔记】Transformer中的LayerNorm是对同一样本的单个patch下的所有维度进行正则化：而传统的LayerNorm是对一个batch中的同一个样本的所有channels进行正则化。
Transformer中的layer norm(包含代码解释)
weixin_42596778的博客
12-07 2952
在transformer中存在add&norm操作，add操作很简单，就是把注意力矩阵和原来的矩阵相加，也就是残差链接，可以有效减少梯度消失。如下图所示，为layer norm的解释图，可以看出layer norm是针对一个token来做的归一化操作。通过输出上的对比我们发现了，使用torch来LN后的EM和我们手动来对Token进行LN的数值一样，说明了LN就是对Token来进行归一会操作的。具体的实现，我们来看下面这段代码，
transformer里的layer-norm理解
OraNgeGreEn的博客
12-02 3719
感谢沐神的讲解。 以往由于深度网络造成的参数波动大，担心梯度受此影响使用batch-norm将其标准化减小参数震动。 时序的翻译任务中，样例长短不一，由词语翻译而成的含义向量应该都是在同一个规模水平的上向量，如果仍然使用batch-norm，由于为了补齐长短不一的样例而添加进去的0使得较长序列中词语的含义向量规模相对变小，较短序列中的词转换为含义向量的规模相对变大。平白无故增添了误差抖动。 使用layer-norm保证每个序列中词语转成的含义向量在同一规模上。 ...
【大模型优化】深入理解 Pre-LayerNorm ：让 Transformer 训练更稳
weixin_41645791的博客
05-22 1301
超深 Transformer 与大语言模型（LLM）时代，归一化策略直接决定了模型能否稳定收敛、推理性能能否最大化。把归一化层从 “残差之后” 挪到 “子层之前”（Pre-LayerNorm，Pre-LN），再将传统 LayerNorm 简化为 RMSNorm——只做均方根缩放、不再减均值——是 GPT-3、LLaMA-4、DeepSeek-V3 等主流 LLM 的标准做法。Pre-LN 让每一层在进入注意力或前馈前就保持单位尺度，显著缓解梯度爆炸/消失；RMSNorm 进一步减少 7-64 % 归一化 F
Transformer归一化技术解析：Pre-Norm/Post-Norm与LayerNorm/RMSNorm的演进与选择
qq_54445177的博客
04-08 1695
Transformer归一化技术解析：Pre-Norm/Post-Norm与LayerNorm/RMSNorm的演进与选择
为什么Transformer架构中选择LayerNorm而非BatchNorm
weixin_52056073的博客
03-09 497
简单记录学习~
LayerNorm是Transformer的最优解吗？
夕小瑶科技说
04-07 6168
一只小狐狸带你解锁 炼丹术&NLP秘籍前言众所周知，无论在CV还是NLP中，深度模型都离不开归一化技术（Normalization）。在CV中，深度网络中一般会嵌入批归一化（...
10分钟搞清楚为什么Transformer中使用LayerNorm而不是BatchNorm
深数研究院
09-20 2575
Normalization技术旨在应对内部协变量偏移问题，它的核心在于将数据调整到一个统一的标准，以便进行有效的比较和处理。为了实现这一目标，***我们需要确保参与归一化的数据点在本质上是可比的。***(记住这句话就可以了)
为什么Transformer使用LayerNorm而不是BatchNorm？
weixin_63866037的博客
01-13 1606
在深度学习的Transformer架构中，有一个有趣的细节是它使用了Layer Normalization（）而非Batch Normalization（这两种归一化方法在不同的神经网络架构中都发挥着重要的作用，但为什么Transformer选择了LayerNorm呢？让我们来一探究竟。
Transformer 代码剖析11 - Layer Normalization（pytorch实现）
lczdyx的博客
03-01 1175
Layer Normalization原理与实现剖析
为什么Transformer要用LayerNorm？
weixin_40920183的博客
11-05 6459
来源：知乎文章仅作学术分享，著作权归属原作者，侵删深海（阿里巴巴算法工程师）回答：Batch Normalization 也是可以用的，但为什么不用，我们来分析一下问题。我们回到RNN，R...
IT巨头裁员！有部门裁了80%，要求自愿离职的员工站出来...
阿木寺的博客
03-11 370
点击下方卡片，关注“CVer”公众号AI/CV重磅干货，第一时间送达2024届春招和2025届暑期实习已经开始了！大家一定要抓住校招机会！Amusi 强烈推荐大家加入汇集今年的求职群，已汇集数千人！最新校招、实习、社招、教职信息、大厂面经和企业内推全都有！还可以跟 Amusi 一对一咨询问答！强烈推荐入群学习！在此CVer特别赠送10张AI算法岗求职群的50元优惠券！今年最大的优惠力度！今年...
Transformer为什么使用LayerNorm而不是BatchNorm?
2401_85328934的博客
10-22 1475
层归一化(Layer normalization ) 是Transformer模型中的一项重要技术，它通过对每一层的输入进行归一化，帮助稳定和加速训练。无论输入的规模或分布如何，它都能确保模型处理信息的一致性。在自注意力机制、多头注意力机制和位置编码等概念的基础上，层归一化在提高Transformer的效率和性能方面发挥着关键作用，使它们更加强大，能够处理复杂的任务。在本博客中，我们将深入探讨层归一化这一Transformer模型中的重要组成部分。
第十章（4）：Transformer之Layer Normalization与Transformer整体结构
安静到无声
10-27 2109
按照顺序将要介绍Layer Normalization，谈起这个模块，就会想起CV领域比较重要BN层 ，被称为批归一化，它具有加快训练速度、防止过拟合等优点。可是，在NLP领域应用更为广泛的是Layer Normalization。在最后我们介绍Encoder和Deconder的整体结构。
transformer中layernorm
03-19
<think>嗯，好的，用户现在问的是Transformer中的LayerNorm，也就是层归一化。我需要先回忆一下相关知识，确保自己理解正确，然后再组织语言用中文解释清楚。 首先，用户之前已经问过关于多头注意力中的qkv变换，现在转向LayerNorm，可能是在学习Transformer结构的不同部分。用户可能是刚开始接触深度学习模型，特别是Transformer，所以需要基础的解释，同时也要结合代码或实现细节，因为之前的问题涉及代码层面的理解。 LayerNorm在Transformer中出现在两个地方：每个子层（比如自注意力和前馈网络）之后，以及残差连接之前。它的作用是对输入进行归一化，使得训练更稳定，收敛更快。但用户可能想知道更具体的细节，比如与BatchNorm的区别，为什么Transformer用LayerNorm，具体怎么计算的，还有它的位置（Pre-LN还是Post-LN）的影响。 接下来，我需要分步骤解释： 1. **LayerNorm的基本概念**：解释归一化的目的，对比BatchNorm，强调LayerNorm是对同一样本的不同特征进行归一化，而不是同一特征在不同样本间。这在序列模型中尤其重要，因为每个样本的长度可能不同，BatchNorm可能不稳定。 2. **LayerNorm在Transformer中的位置**：比如在原始论文中是Post-LN（残差连接之后），但现在很多实现用Pre-LN（残差之前），需要说明两者的差异和影响，比如训练深度模型时的梯度问题。 3. **数学公式**：给出LayerNorm的公式，包括减去均值，除以标准差，再应用缩放和平移参数。需要用LaTeX，按照用户之前的要求，行内公式用$...$，独立公式用$$...$$。比如： $$ \text{LayerNorm}(x) = \gamma \cdot \frac{x - \mu}{\sigma + \epsilon} + \beta $$ 这里要解释μ和σ是沿着特征维度计算的，γ和β是可学习的参数。 4. **为什么有效**：缓解内部协变量偏移，稳定训练，允许更深的网络。特别是在Transformer中，由于残差连接和自注意力可能带来的值范围变化，LayerNorm帮助维持数据分布。 5. **实现细节**：比如在PyTorch中的nn.LayerNorm的使用，参数是normalized_shape，通常是d_model（特征维度）。比如输入形状为(batch, seq_len, d_model)，LayerNorm会在最后两个维度上计算均值和方差。 6. **与BatchNorm的对比**：强调BatchNorm在序列长度变化时的问题，比如测试时可能遇到更长的序列，导致统计量不准确。而LayerNorm不受序列长度影响，更适合NLP任务。 用户可能潜在的问题是，为什么Transformer选择LayerNorm而不是其他归一化方法，或者LayerNorm的具体实现步骤。需要确保回答覆盖这些点，并且结构清晰，逐步引导用户理解。 可能需要举例子，比如输入的形状，处理后的变化，参数γ和β的作用。同时要注意之前用户的问题涉及代码，所以可能关联到实际代码中的使用，比如在Transformer的每个子层后应用LayerNorm。 另外，注意用户要求回答结构清晰，帮助逐步解决问题，所以分点解释会比较合适。可能需要用标题分点，但根据用户之前的回答，他们用了###和---来分隔，所以可以沿用类似的格式，但避免使用Markdown，因为现在是在思考过程中。 总结，需要涵盖： - LayerNorm的定义和计算方式 - 在Transformer中的位置和作用 - 与BatchNorm的区别及优势 - 数学公式和代码实现示例 - 有效性的原因 检查是否有遗漏，比如可能用户想知道LayerNorm对模型性能的具体影响，或者训练中的表现，比如是否解决了梯度消失等问题。需要确保回答全面，同时保持简洁易懂。</think>在Transformer中，**LayerNorm（层归一化）** 是一种关键的正则化技术，通过对同一样本的不同特征维度进行归一化，稳定训练过程并提升模型收敛速度。以下是详细解释： --- ### **1. 核心作用** - **稳定梯度**：缓解深层网络中梯度爆炸或消失的问题。 - **加速收敛**：通过归一化输入分布，减少内部协变量偏移（Internal Covariate Shift）。 - **适应动态范围**：Transformer中的自注意力机制输出值范围可能剧烈波动，LayerNorm 将其约束到合理区间。 --- ### **2. 数学定义** 对输入张量 $x$ 沿**特征维度**（通常是最后一维）计算均值 $\mu$ 和方差 $\sigma^2$，再进行缩放和平移： $$ \text{LayerNorm}(x) = \gamma \cdot \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} + \beta $$ 其中： - $\gamma$ 和 $\beta$：可学习的缩放因子和偏置项 - $\epsilon$：防止除零的小常数（如 $10^{-5}$） --- ### **3. 在Transformer中的位置** 原始论文采用 **Post-LayerNorm**（残差连接后归一化）： $$ x_{\text{out}} = \text{LayerNorm}(x + \text{Sublayer}(x)) $$ 但现代实现（如GPT、T5）常改用 **Pre-LayerNorm**（残差连接前归一化），缓解梯度消失： $$ x_{\text{out}} = x + \text{Sublayer}(\text{LayerNorm}(x)) $$ --- ### **4. 与BatchNorm的对比** | **特性** | **LayerNorm** | **BatchNorm** | |----------------|----------------------------|----------------------------| | 归一化维度 | 沿特征维度（样本内） | 沿批量维度（跨样本同一特征）| | 适用场景 | 变长序列（如NLP） | 固定长度输入（如CV） | | 训练/测试差异 | 无依赖，推理稳定 | 依赖训练时的移动平均值 | --- ### **5. 代码示例（PyTorch）** ```python import torch.nn as nn d_model = 512 # 特征维度 layer_norm = nn.LayerNorm(d_model) # 输入形状: (batch_size, seq_len, d_model) x = torch.randn(32, 10, d_model) output = layer_norm(x) # 归一化后形状不变 ``` --- ### **6. 直观理解** 假设输入是一个句子中的单词向量： - **未归一化时**：某些特征维度值可能过大/过小，导致后续计算不稳定。 - **归一化后**：所有特征维度被调整到均值为0、方差为1的分布，再通过 $\gamma$ 和 $\beta$ 恢复模型表达能力。 --- ### **7. 为什么Transformer必须用LayerNorm？** - **序列长度可变性**：BatchNorm在序列任务中因长度变化统计量不稳定。 - **自注意力特性**：注意力分数受点积规模影响，LayerNorm约束输入范围，使softmax更稳定。 - **残差连接协同**：与残差结构配合，允许训练极深层网络（如BERT有24层以上）。 --- ### **总结** LayerNorm是Transformer稳定训练的基石，通过特征维度的归一化，使模型对参数初始化和学习率更鲁棒，同时与残差连接共同解决了深层网络训练的难题。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值