1 实验目的
- 进一步掌握IOSDATA的原理及应用;
- 用MATLAB实现IOSTDATA算法
2 实验内容
(1) 选择某些初始值。可选不同的参数指标,也可在迭代过程中人为修改,以将N个模式样本按指标分配到各个聚类中心中去。
(2) 计算各类中诸样本的距离指标函数。
(3)~(5)按给定的要求,将前一次获得的聚类集进行分裂和合并处理((4)为分裂处理,(5)为合并处理),从而获得新的聚类中心。
(6) 重新进行迭代运算,计算各项指标,判断聚类结果是否符合要求。经过多次迭代后,若结果收敛,则运算结束。
3实验原理
第一步:输入NN个模式样本{xi,i=1,2,…,N}{xi,i=1,2,…,N}
预选NcNc个初始聚类中心{z1,z2,…zNc}{z1,z2,…zNc},它可以不等于所要求的聚类中心的数目,其初始位置可以从样本中任意选取。
预选:KK = 预期的聚类中心数目;
θNθN = 每一聚类域中最少的样本数目,若少于此数即不作为一个独立的聚类;
θSθS = 一个聚类域中样本距离分布的标准差;
θcθc= 两个聚类中心间的最小距离,若小于此数,两个聚类需进行合并;
LL= 在一次迭代运算中可以合并的聚类中心的最多对数;
II = 迭代运算的次数。
第二步:将NN个模式样本分给最近的聚类SjSj,假若Dj=min{∥x−zi∥,i=1,2,⋯Nc}Dj=min{‖x−zi‖,i=1,2,⋯Nc}
,即||x−zj||||x−zj||的距离最小,则x∈Sjx∈Sj。
第三步:如果SjSj中的样本数目Sj<θN,则取消该样本子集,此时Nc减去1。
(以上各步对应基本步骤(1))
第四步:修正各聚类中心
zj=1Nj∑x∈Sjx,j=1,2,⋯,Nczj=1Nj∑x∈Sjx,j=1,2,⋯,Nc
第五步:计算各聚类域Sj中模式样本与各聚类中心间的平均距离
D¯j=1Nj∑x∈Sj∥x−zj∥,j=1,2,⋯,NcD¯j=1Nj∑x∈Sj‖x−zj‖,j=1,2,⋯,Nc
第六步:计算全部模式样本和其对应聚类中心的总平均距离
D¯=1N∑j=1NNjD¯jD¯=1N∑j=1NNjD¯j
(以上各步对应基本步骤(2))
第七步:判别分裂、合并及迭代运算
- 若迭代运算次数已达到I次,即最后一次迭代,则置θc =0,转至第十一步。
- 若Nc≤K2Nc≤K2
,即聚类中心的数目小于或等于规定值的一半,则转至第八步,对已有聚类进行分裂处理。 - 若迭代运算的次数是偶数次,或Nc≥2KNc≥2K
,不进行分裂处理,转至第十一步;否则(即既不是偶数次迭代,又不满足Nc≥2KNc≥2K),转至第八步,进行分裂处理。
(以上对应基本步骤(3))
第八步:计算每个聚类中样本距离的标准差向量
σj=(σ1j,σ2j,…,σnj)Tσj=(σ1j,σ2j,…,σnj)T
其中向量的各个分量为
σij=1Nj∑k=1Nj(xik−zij)2−−−−−−−−−−−−−−−⎷σij=1Nj∑k=1Nj(xik−zij)2
式中,i = 1, 2, …, n为样本特征向量的维数,j = 1, 2, …, Nc为聚类数,Nj为Sj中的样本个数。
第九步:求每一标准差向量{σj, j = 1, 2, …, Nc}中的最大分量,以{σjmax, j = 1, 2, …, Nc}代表。
第十步:在任一最大分量集{σjmax, j = 1, 2, …, Nc}中,若有σjmax>θS ,同时又满足如下两个条件之一:
- D¯j>D¯D¯j>D¯和Nj > 2(θN + 1),即Sj中样本总数超过规定值一倍以上,
- Nc≤K2Nc≤K2
则将zj 分裂为两个新的聚类中心和,且Nc加1。 中对应于σjmax的分量加上kσjmax,其中;中对应于σjmax的分量减去kσjmax。
如果本步骤完成了分裂运算,则转至第二步,否则继续。
(以上对应基本步骤(4)进行分裂处理)
第十一步:计算全部聚类中心的距离
Dij=||zi−zj||,i=1,2,…,Nc−1,j=i+1,…,NcDij=||zi−zj||,i=1,2,…,Nc−1,j=i+1,…,Nc
第十二步:比较Dij 与θc 的值,将Dij <θc 的值按最小距离次序递增排列,即
{Di1j1,Di2j2,…,DiLjL}{Di1j1,Di2j2,…,DiLjL}
式中Di1j1<Di2j2<…<DiLjLDi1j1<Di2j2<…<DiLjL。
第十三步:将距离为DikjkDikjk的两个聚类中心ZikZik和ZjkZjk合并,得新的中心为:
z∗k=1Nik+Njk[Nikzik+Njkzjk],k=1,2,⋯,Lzk∗=1Nik+Njk[Nikzik+Njkzjk],k=1,2,⋯,L
式中,被合并的两个聚类中心向量分别以其聚类域内的样本数加权,使Z∗kZk∗为真正的平均向量。
(以上对应基本步骤(5)进行合并处理)
第十四步:如果是最后一次迭代运算(即第I次),则算法结束;否则,若需要操作者改变输入参数,转至第一步;若输入参数不变,转至第二步。
在本步运算中,迭代运算的次数每次应加1。
4实验步骤
实现代码:
close all;
clear all;
clc;
%数据导入
in_data = load('SelfOrganizationSimulation.dat'); %导入数据
x = in_data; %待分类样本
%给数据添加类别标签
label = [ones(10,1);ones(10,1)*2;ones(10,1)*3];
in_data = [in_data,label];
%-------------ISODATA---------------%
Imax = 6;%迭代次数
Nc =5;%预选初始聚类中心个数
% %记录聚类数目
record = zeros(1,Imax);
%随机选取Nc个初始聚类中心
r = randperm(30);
for i=1:Nc
center(i,:) = x(r(i),:);
end
clear i;
clear r;
[n,d] = size(x);%n为数据行数,d为数据列数
I=1;
while I<Imax
%step1:初始化
T = input('是否要设置输入参数?是请输入‘1’,否请输入‘0’:T=');
if(T==1)
K = input('请输入预期聚类中心数目:K=');%预期的聚类中心个数
Qn = input('请输入每一聚类中最少样本数:Qn=');%每一类中最少的样本数目
Qs = input('请输入一个聚类中样本距离分布的标准差:Qs=');%一个聚类中样本距离分布的标准差
Qc = input('请输入两类聚类中心间的最小距离:Qc=');%两类聚类中心间的最小距离
%L = input('请输入一次迭代中可以合并聚类中心的最多个数:L=');%一次迭代中可以合并聚类中心的最多个数
end
% K = 3;%预期的聚类中心个数
% Qn = 5;%每一类中最少的样本数目
% Qs = 1.8;%一个聚类中样本距离分布的标准差
% Qc = 1.5;%两类聚类中间的最小距离
seperate = 1; %分裂标识,为1时可进入分裂循环,为0时跳出分裂循环
while(seperate==1)
% disp('正在运行while循环');
%step2:将待分类数据分别分配给距离最近的聚类中心
distance = zeros(n,Nc);%n为x的行数,NC为初始聚类中心个数
for i=1:n
for j=1:Nc
distance(i,j) = norm(x(i,:)-center(j,:));%遍历到聚类中心的欧氏距离
end
end
[m,index] = min(distance,[],2);%逻辑索引index为1或0;
class = index;
clear m;
clear index;
clear distance;%删除m,index,distance;
%统计各子集的样本数目
num = zeros(1,Nc);
for i=1:Nc
index = find(class==i);%找到第i行的索引和值;
num(i) = length(index);%子集i的样本数目
end
clear i;
clear index;
%step3:取消样本数目小于Qn的子集
index = find(num>=Qn);%Qn为每一类中最少样本数目;
Nc = length(index);
center_hat = zeros(Nc,d);
for i=1:Nc
center_hat(i,:) = center(index(i),:);
end
center = center_hat;
clear center_hat;
clear index;
%重新将待分类数据分别分配给距离最近的聚类中心
distance = zeros(n,Nc);
for i=1:n
for j=1:Nc
distance(i,j) = norm(x(i,:)-center(j,:));
end
end
[m,index] = min(distance,[],2);
class = index;
clear m;
clear index;
clear distance;
%step4:修正聚类中心
new_center = zeros(Nc,d);
num = zeros(1,Nc);
for i=1:Nc
index = find(class==i);
num(i) = length(index);%子集i的样本数目
new_center(i,:) = mean(x(index,:));%子集i的聚类中心
end
center = new_center;
clear new_center;
clear index;
%step5:计算各子集中的样本到中心的平均距离dis
%step6:计算全部模式样本与其对应聚类中心总平均距离ddis
dis = zeros(1,Nc);
ddis = 0;
for i=1:Nc
index = find(class==i);
for j=1:num(i)
dis(i) = dis(i)+norm(x(index(j),:)-center(i,:));
end
ddis =ddis+dis(i);
dis(i) = dis(i)/num(i);
end
ddis = ddis/n;
clear index;
%step7:判断分裂,合并及迭代
%如果迭代次数到达Imax次,置Qc=0,跳出循环至step14
if I==Imax %(1)
Qc = 0;
break;
end
if (Nc<=K/2) %(2)如果不进入分裂则跳到step11,合并
seperate = 1;
end
if(mod(I,2)==0|Nc>=2*K) %(3)
break;
else
seperate = 1;
end
%step8:分裂
%计算每个聚类中,各样本到中心的标准差向量
sigma = zeros(Nc,d);%sigma(i)代表第i个聚类的标准差向量
for i=1:Nc
index = find(class==i);
for j=1:num(i)
sigma(i,:) = sigma(i,:)+(x(index(j),:)-center(i,:)).^2;
end
sigma(i,:) = sqrt(sigma(i,:)/num(i));
end
clear index;
%step9:求各个标准差{sigma_j}的最大分量
[sigma_max,max_index] = max(sigma,[],2);
%step10:分裂
k=0.5;%分裂聚类中心时使用的系数
temp_Nc = Nc;
for i=1:temp_Nc
if sigma_max(i)>Qs&((dis(i)>ddis&num(i)>2*(Qn+1))|Nc<=K/2)
Nc = Nc+1;
%将z(i)分裂为两个新的聚类中心
center(Nc,:) = center(i,:);
center(i,max_index(i)) = center(i,max_index(i))+k*sigma_max(i);
center(Nc,max_index(i)) =center(Nc,max_index(i))+k*sigma_max(i);
end
end
record(I) = Nc;
%绘制聚类效果图
figure;
for i=1:30
if class(i)==1
plot3(x(i,1),x(i,2),x(i,3),'r*');%红色*表示第1簇
hold on;
end
if class(i)==2
plot3(x(i,1),x(i,2),x(i,3),'b+');%篮色+表示第2簇
hold on;
end
if class(i)==3
plot3(x(i,1),x(i,2),x(i,3),'go');%绿色o表示第3簇
hold on;
end
if class(i)==4
plot3(x(i,1),x(i,2),x(i,3),'kx');%黑色x表示第4簇
hold on;
end
if class(i)==5
plot3(x(i,1),x(i,2),x(i,3),'md');%品红色菱形表示第5簇
hold on;
end
end
title('聚类效果图');
I = I+1;
end
% disp('正在运行合并');
if(I<Imax);
%% step11:合并
%计算全部聚类中心间的距离
center_Dis = zeros(Nc-1,Nc);
for i=1:Nc
for j=i+1:Nc
center_Dis(i,j) = norm(center(i,:)-center(j,:));
end
end
%% step12,13:如果距离最小的两个中心之间距离小于Qc,将其合并
%找出距离最近的两个中心
min_Dis = center_Dis(1,3); %最小距离
min_index = [1,3]; %距离最近的两个中心的标号
for i=1:Nc
for j=i+1:Nc
if center_Dis(i,j)<min_Dis
min_Dis = center_Dis(i,j);
min_index = [i,j];
end
end
end
if min_Dis<Qc
%合并距离最近的两个中心
%合并产生的新中心为
new_center = (center(min_index(1),:)*num(min_index(1))+center(min_index(2),:)*num(min_index(2)))/(num(min_index(1))+num(min_index(2)));
temp_center = zeros(1,Nc);
temp_center = center;
temp_center(min_index(1),:) = new_center;
temp_center(min_index(2),:) = center(Nc,:);
Nc = Nc-1;%聚类数目减1
center = temp_center(1:Nc,:);
clear temp_center
end
end
record(I)= Nc;
I =I+1
%绘制聚类效果图
hold off;
for i=1:30
if class(i)==1
plot3(x(i,1),x(i,2),x(i,3),'r*');%红色*表示第1簇
hold on;
end
if class(i)==2
plot3(x(i,1),x(i,2),x(i,3),'b+');%篮色+表示第2簇
hold on;
end
if class(i)==3
plot3(x(i,1),x(i,2),x(i,3),'go');%绿色o表示第3簇
hold on;
end
if class(i)==4
plot3(x(i,1),x(i,2),x(i,3),'kx');%黑色x表示第4簇
hold on;
end
if class(i)==5
plot3(x(i,1),x(i,2),x(i,3),'md');%品红色菱形表示第5簇
hold on;
end
if class(i)==6
plot3(x(i,1),x(i,2),x(i,3),'c.');%青色实心点表示第6簇
hold on;
end
if class(i)==7
plot3(x(i,1),x(i,2),x(i,3),'yp');%黄色五角星表示第7簇
hold on;
end
end
title('聚类效果图');
end
Nc
center
class'
%%
% figure(2);
% plot(record);
% title('聚类数目变化曲线');
% %统计聚类效果
% %result(i,j)代表第i类数据被聚类至第j簇的数量
% result = zeros(3,Nc);
% clear m;
% for m=1:3
% for i=(50*(m-1)+1):1:50*m
% for j=1:Nc
% if class(i)==j
% result(m,j) = result(m,j)+1;
% end
% end
% end
% end
% %计算准确率,召回率,F值
% %P(i,j)代表第i类数据与第j簇相应的准确率
% %R(i,j)代表第i类数据与第j簇相应的召回率
% for i=1:3
% for j=1:Nc
% P(i,j) = result(i,j)/num(j);
% R(i,j) = result(i,j)/50;
% F(i,j) = 2*P(i,j)*R(i,j)/(P(i,j)+R(i,j));
%
% % disp('F(i,j)代表第i类数据与第j簇相应的F值');
% % F
% disp('FF(i)代表第i类数据的F值');
% FF = max(F,[],2)
% disp('整个聚类结果的F值')
% F_final = mean(FF);
实验结果:
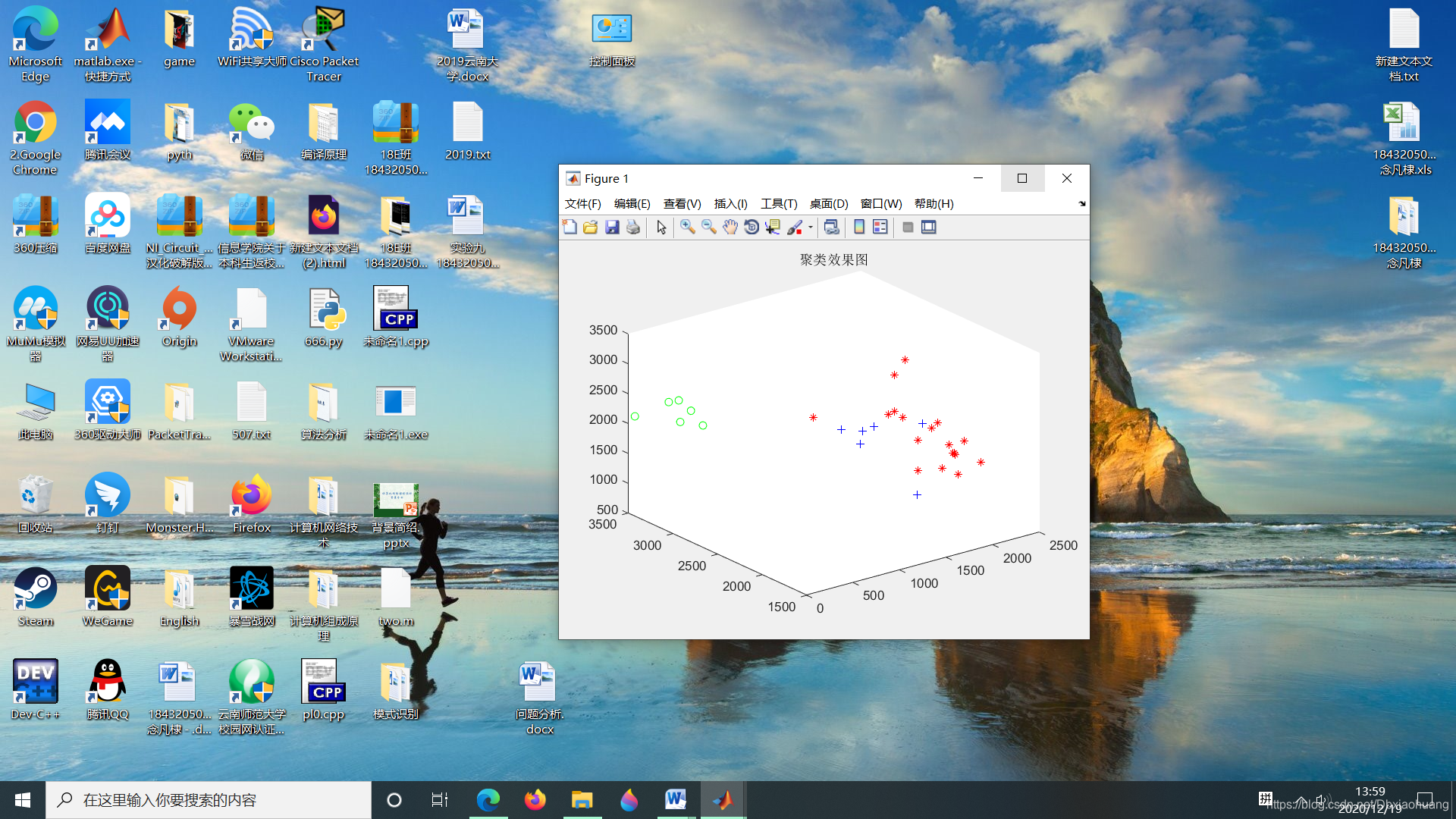




 本文详细介绍了ISODATA聚类算法的原理和MATLAB实现过程,包括选择初始值、计算距离指标、分裂和合并聚类中心等步骤。通过迭代优化,最终确定聚类结果。实验中还提供了交互式输入参数的选项,允许用户根据需求调整参数以影响聚类效果。
本文详细介绍了ISODATA聚类算法的原理和MATLAB实现过程,包括选择初始值、计算距离指标、分裂和合并聚类中心等步骤。通过迭代优化,最终确定聚类结果。实验中还提供了交互式输入参数的选项,允许用户根据需求调整参数以影响聚类效果。
















 6872
6872

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








