LeetCode 221. 最大正方形-优快云博客

本文针对LeetCode221题——最大正方形进行了解析，介绍了如何通过动态规划的方法来解决该问题，并给出了具体实现的代码示例。通过分析二维矩阵中的'1'构成的最大正方形面积，提出了一种有效的解决方案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

LeetCode 221. 最大正方形

文章目录

题目描述
一、基础框架
二、解题报告
总结

题目描述

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

原题连接
链接：https://leetcode-cn.com/problems/maximal-square/

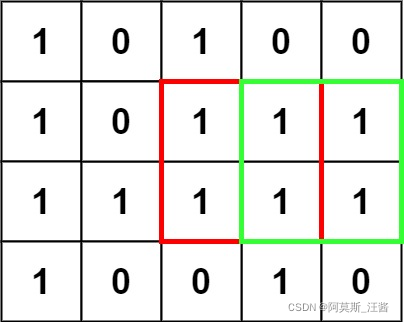
在这里插入图片描述

输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

一、基础框架

二、解题报告

1.思路分析

1、一开始是比较懵逼的，需要谨慎思考
2、注意条件数组含有 1 和0。只处理关于1的数据
3、需要求最优解联想到贪心和动态规划
4、二维数组果断动态规划
双层循环找到等于1的元素记录边长；

2.时间复杂度

3.代码示例

tips：

class Solution {
 public int maximalSquare(char[][] matrix) {
        int row = matrix.length;
        int col = matrix[0].length;
        //终止程序
        if(matrix == null || row < 1 || col < 1){
            return 0;
        }
        int maxSize = 0;

        int [][] dp = new int[row + 1][col + 1];
        for(int i = 0 ; i < row;i ++ ){
            for(int j = 0; j < col ; j ++){
                if(matrix[i][j] == '1'){
                    dp[i + 1][j + 1] = Math.min(Math.min(dp[i + 1][j],dp[i][j + 1]),dp[i][j]) + 1;
                    maxSize = Math.max(maxSize,dp[i + 1][j + 1]);
                }
            }
        }
        return maxSize * maxSize;
    }
}