[数据结构] AVLTree平衡二叉搜索树的模拟实现

定义

• 它或者是空树，或者是具有以下性质的二叉搜索树：
  左右子树高度之差(简称平衡因子)的绝对值不超过1(可以取值为：-1/0/1)；
  并且，它的左右子树都是AVL树。

效率

• 如果一颗AVL有n个结点，那么其高度可保持在logN，搜索时间复杂度O(logN)。

模拟实现

1）实现基本框架

定义结点

• 采用三叉链表的形式定义树的结点，用pair存放数据，增加平衡因子成员变量；

其构造、拷贝构造、赋值重载、析构函数同BSTree

template<class K, class V>
	struct AVLTreeNode{
		AVLTreeNode<K, V>* _left;
		AVLTreeNode<K, V>* _right;
		AVLTreeNode<K, V>* _parent;
		int _bf;  //平衡因子
		pair<K, V> _kv;  //数据

		AVLTreeNode(const pair<K, V>& kv)
			:_left(nullptr),
			_right(nullptr),
			_parent(nullptr),
			_bf(0),
			_kv(kv){
		}
	}

2）实现基本操作

insert插入操作

• 先找待插入结点的位置（按key值比较），结点插入后自底向上更新平衡因子的值；
• 平衡因子更新后会出现三种情况：

1. 不需要继续更新
2. 需要继续向上更新
3. 已经出现不平衡的现象，需要对子树进行旋转处理
4. 更新出现了错误，断言退出；

pair<node*, bool> insert_1(const pair<K, V>& kv)
		{
			if (_root == nullptr){
				_root = new node(kv);
				return make_pair(_root, true);
			}

			//1.先找到要插入的位置
			node* parent = nullptr;
			node* cur = _root;
			while (cur != nullptr){
				if (kv.first < cur->_kv.first){
					parent = cur;
					cur = cur->_left;
				}
				else if (kv.first > cur->_kv.first){
					parent = cur;
					cur = cur->_right;
				}
				else{  //碰到了相等的结点数据，无法插入
					return make_pair(cur, true);
				}
			}//cur为空，找到了待插入位置

			//2.构造kv结点，插入结点到AVL树中
			cur = new node(kv);
			if (kv.first < parent->_kv.first){
				parent->_left = cur;
				cur->_parent = parent;
			}
			else{
				parent->_right = cur;
				cur->_parent = parent;
			}

			//3.自底向上更新平衡因子
			while (cur != _root){
				//3.1先更新parent的平衡因子
				if (cur == parent->_left)
					parent->_bf--;
				else{
					parent->_bf++;
				}

				//3.2判断是否需要继续向上更新
				if (parent->_bf == 0){
					break;
				}
				else if (parent->_bf == 1 || parent->_bf == -1){
					//继续向上更新
					cur = parent;
					parent = parent->_parent;
				}
				else if (parent->_bf == 2 || parent->_bf == -2){
					//parent所在子树已经不平衡，需要旋转处理
					if (parent->_bf == -2){
						if (cur->_bf == -1)
							//右单旋
							RotateR(parent);
						else
							RotateLR(parent);
					}
					else{
						if (cur->_bf == 1)
							//左单旋
							RotateL(parent);
						else
							RotateRL(parent);
					}
					break;  //旋转完成之后跳出循环
				}
				else{
					//平衡因子已经出现了错误
					assert(false);
				}
			}
			return make_pair(cur, true);  //插入成功
		}

四种旋转处理操作

• 以右单旋和左右双旋两种情况为例：

右单旋

• 单旋后，更新parent、subL/subR的平衡因子的值为0
  

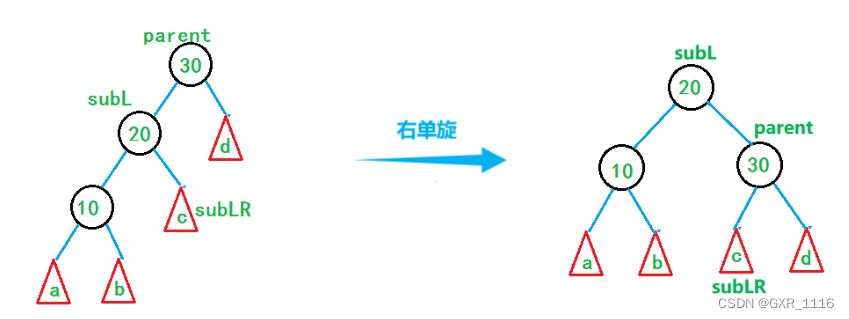
void RotateR(node* parent){
			node* subL = parent->_left;
			node* subLR = subL->_right;

			parent->_left = subLR;
			if (subLR != nullptr){
				subLR->_parent = parent;
			}

			subL->_right = parent;
			node* parentparent = parent->_parent;
			parent->_parent = subL;

			parent->_bf = 0;
			subL->_bf = 0;

			if (parent == _root){
				_root = subL;
				_root->_parent = nullptr;
			}
			else{
				if (parent == parentparent->_left){
					parentparent->_left = subL;
				}
				else{
					parentparent->_right = subL;
				}
				subL->_parent = parentparent;
			}

		}

左单旋逻辑同上

左右双旋

• 双旋后，根据旋转前subLR/subRL平衡因子的值更新parent、subL、subLR的值
  

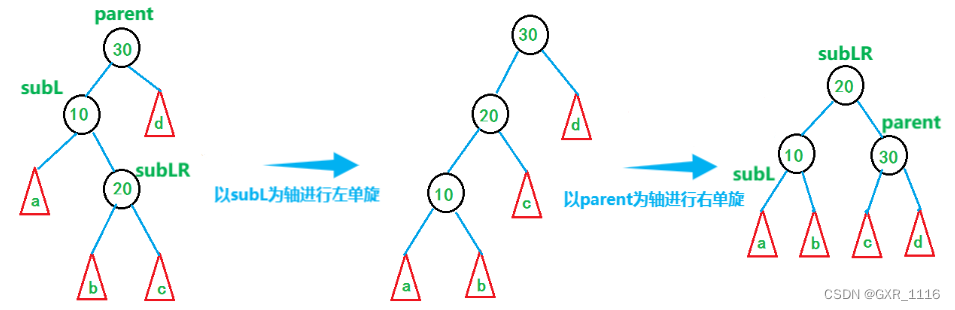
	void RotateLR(node* parent){
			node* subL = parent->_left;
			node* subLR = subL->_right;

			int bf = subLR->_bf;  //旋转之前保留subLR的平衡因子的值

			RotateL(parent->_left);
			RotateR(parent);

			if (bf == 1){  
				parent->_bf = 0;
				subL->_bf = -1;
				subLR->_bf = 0;
			}
			else if (bf == -1){
				parent->_bf = 1;
				subL->_bf = 0;
				subLR->_bf = 0;
			}
			else if (bf == 0){
				parent->_bf = 0;
				subL->_bf = 0;
				subLR->_bf = 0;
			}
			else{
				assert(false);
			}
		}

右左双旋逻辑同上

find查找操作，同BSTree

重载operator[ ]

V& operator[](const K& key){
			pair<node*, bool> ret = insert_1(make_pair(key, V()));
			return ret.first->_kv.second;
		}

判定是否是AVLTree

验证其是否为二叉搜索树

验证其是否为平衡树

		bool _isBalance(node* root){
			if (root == nullptr)
				return true;
			int left_hight = _hight(root->_left);
			int right_hight = _hight(root->_right);
			if (right_hight - left_hight != root->_bf)
				cout << "error..." << endl;
			return abs(right_hight - left_hight) < 2 && _isBalance(root->_left) && _isBalance(root->_right);
		}
		
		int _hight(node* root){
			if (root == nullptr)
				return 0;
			int left_hignt = _hight(root->_left);
			int right_hight = _hight(root->_right);
			return left_hignt > right_hight ? left_hignt + 1 : right_hight + 1;
		}