树的直径 树的重心

一棵树的直径就是这棵树上存在的最长路径。现在有一棵n个节点的树，现在想知道这棵树的直径包含的边的个数是多少？

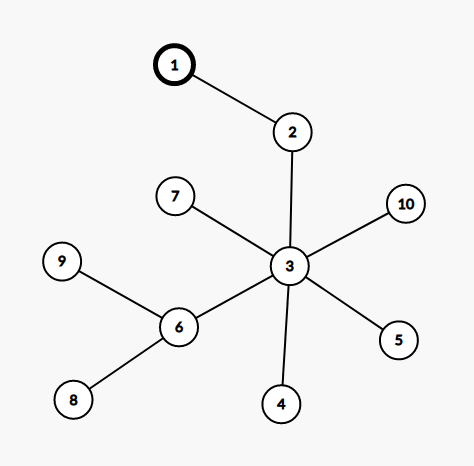
如图所示的数据，这棵树的直径为(1-2-3-6-9)这条路径，包含的边的个数为4，所以答案是4。

Input

第1行：一个整数n，表示树上的节点个数。(1<=n<=100000) 第2-n行：每行有两个整数u,v,表示u与v之间有一条路径。(1<=u,v<=n)

Output

输出一个整数，表示这棵树直径所包含的边的个数。

Sample

Inputcopy	Outputcopy
10 1 2 2 3 3 4 3 5 3 6 3 7 3 10 6 8 6 9	4

#include <iostream>
#include <cmath>
using namespace std;
const int MAXN = 1e5+10;
struct info{
	int to,nt;
}node[MAXN*2];
int pre[MAXN],cnt,ans;
void add(int x,int y)
{
	cnt++;
	node[cnt].to = y;
	node[cnt].nt = pre[x];
	pre[x] = cnt;
}
int dfs(int x,int fa)
{
	int res = 0,m1 = 0,m2 = 0;
	for(int i = pre[x];i;i = node[i].nt){
		int to = node[i].to;
		if(to == fa) continue;
		int d = dfs(to,x) + 1;
		res = max(res,d);
		if(d >= m1){
			m2 = m1;
			m1 = d;
		}
		else if(d > m2)
			m2 = d;
	}
	ans = max(ans,m1+m2);
	return res;
}
int main()
{
	int n,t1,t2;
	scanf("%d",&n);
	for(int i = 1;i < n;i++){
		scanf("%d %d",&t1,&t2);
		add(t1,t2);
		add(t2,t1);
	}
	dfs(1,0);
	printf("%d",ans);
	return 0;
 }