LOJ6066-哈希，dfs序（括号序列）

LOJ6066

题目描述

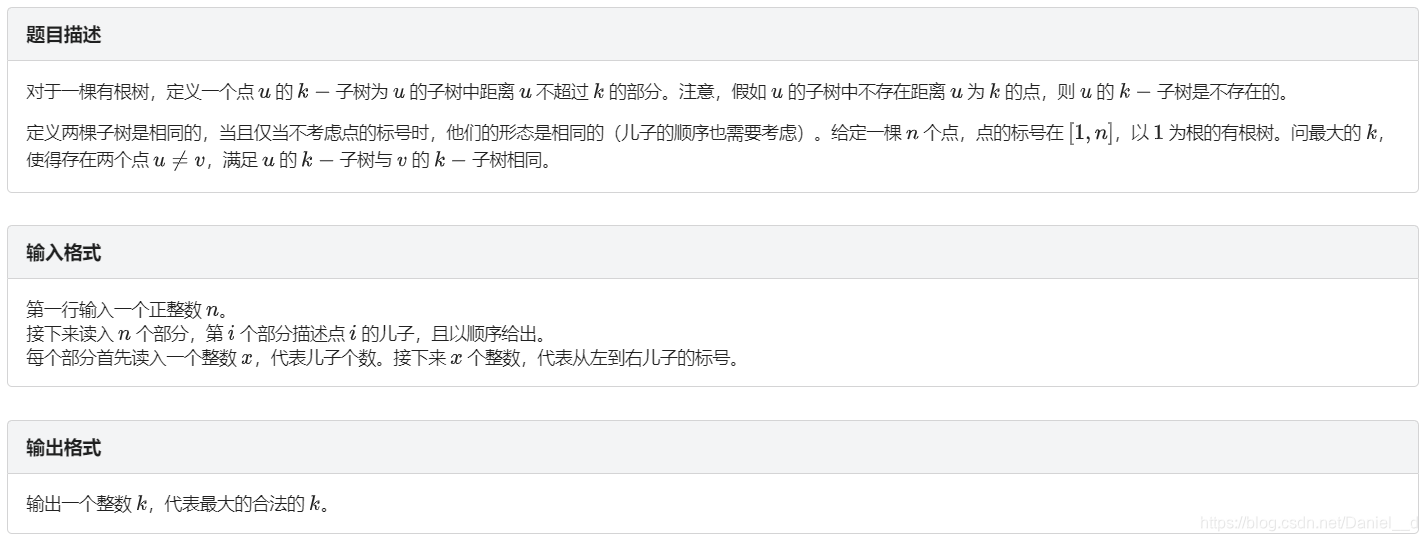
题解

首先想到的是树哈希，但其实不然，因为本题说儿子的顺序也要一致，因此我们考虑dfs序（即树的括号序列），我们将整棵树的$dfs$序转换为一个序列，对其进行哈希，然后注意到$k$值是具有二分单调性的（证明很显然），于是我们对$k$值进行二分，然后$check$。
至于$check$的方法就是：假设当前二分值为mid，那么我们将所有点挂在它的$mid+1$级祖先上（开栈），这样每次计算每个节点的$u-mid$子树时可以方便加入合法的一段序列

代码

#include<bits/stdc++.h>
#include <tr1/unordered_map>
#define M 200009//要开双倍,因为dfs序 
#define LL unsigned long long
using namespace std;
using namespace tr1;
int read(){
	int f=1,re=0;
	char ch;
	for(ch=getchar();!isdigit(ch)&&ch!='-';ch=getchar());
	if(ch=='-'){f=-1,ch=getchar();}
	for(;isdigit(ch);ch=getchar()) re=(re<<3)+(re<<1)+ch-'0';
	return re*f; 
}
const LL h=37;
LL nxt[M],first[M],to[M],tot,cnt,n,num[M],len[M],ed[M],sta[M],top;
LL val[M],mi[M],has[M];
vector<LL>son[M];
unordered_map<LL,LL>mp;
void add(int x,int y){
	nxt[++tot]=first[x];
	first[x]=tot;
	to[tot]=y;
}
void dfs1(int x){//求括号序列 
	num[x]=++cnt,val[cnt]=133;
	for(int i=first[x];i;i=nxt[i]){
		int v=to[i];
		dfs1(v);
		len[x]=max(len[x],len[v]);
	}ed[x]=++cnt,len[x]++,val[cnt]=233; 
}
void dfs2(int u,int k){//将点挂在k+1级祖先上 
	sta[++top]=u;
	if(top-1>k) son[sta[top-k-1]].push_back(u);
	for(int i=first[u];i;i=nxt[i]){
		int v=to[i];
		dfs2(v,k);
	}top--;
}
LL gethas(int l,int r){
	return has[r]-has[l-1]*mi[r-l+1];
}
bool check(int mid){
	mp.clear();
	for(int i=1;i<=n;i++) son[i].clear();
	dfs2(1,mid);
	for(int i=1;i<=n;i++)
		if(len[i]>mid){
			int l=num[i],r;LL ans=0;
			for(int j=0;j<son[i].size();j++){
				r=num[son[i][j]]-1;
				ans=ans*mi[r-l+1]+gethas(l,r);
				l=ed[son[i][j]]+1;
			}r=ed[i];
			ans=ans*mi[r-l+1]+gethas(l,r);
			if(mp.count(ans)) return true;
			mp[ans]=1;
		}return false;
	
}
int main(){
	n=read();
	for(int i=1;i<=n;i++){
		int x=read(),y;
		for(int j=1;j<=x;j++) y=read(),add(i,y);
	}dfs1(1),mi[0]=1;
	for(int i=1;i<=cnt;i++) mi[i]=mi[i-1]*h;
	for(int i=1;i<=cnt;i++) has[i]=has[i-1]*h+val[i];
	int l=2,r=n;
	while(l<r){//满足二分单调性 
		int mid=(l+r+1)>>1;
		if(check(mid)) l=mid;
		else r=mid-1;
	}printf("%d\n",l);
	return 0;
}