java手撕红黑树，左旋、右旋、变色、及红黑树的设计概念

最新推荐文章于 2022-07-11 11:10:26 发布

原创最新推荐文章于 2022-07-11 11:10:26 发布 · 663 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#java #红黑树

java 专栏收录该内容

1 篇文章

订阅专栏

本文介绍了红黑树的基本概念，包括节点结构、插入操作、左旋、右旋规则以及红黑树的平衡策略。通过Java代码展示了插入节点时如何进行旋转和变色，解释了为何进行这些操作以保持树的平衡，并探讨了红黑树的设计理解。

理念：只要你把事情分的足够简单，系统就不会出错。

一、总览：首先我们来看一下一颗简单的树是什么结构。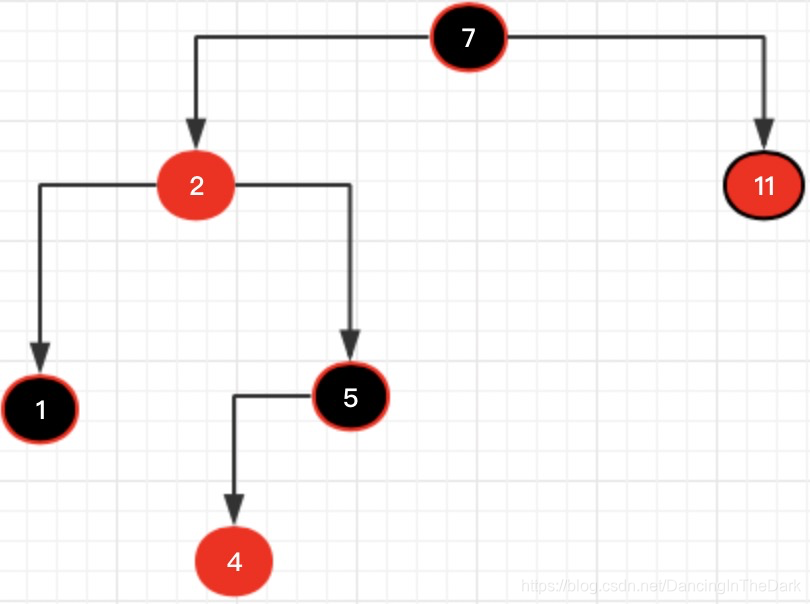

二、节点：很明显，一颗树是由一个个简单的节点组成的，所以要想搞清红黑树，首先熟悉最简单的节点。
为了简化便于理解，每个节点的值用int格式。
红黑树节点的组成：值、左孩子、右孩子、父节点、颜色。用java代码表示如下：

class RBNode{
        int value;
        boolean color;//true = 黑，false = 红
        RBNode farther;
        RBNode left;
        RBNode right;
        }

三、明白了单个节点的结构，我们学习一下树的插入。
   1、找到合适的节点
   2、当前值比节点小且节点左节点为空，插入左孩子位置，反之插入右孩子位置，前提是孩子为空。
   找孩子我们代码用递归的思想去做，首先找的是根节点，在类中是个全局变量root。java代码实现如下。

public void put(int value){
        if(root == null) {
            root = new RBNode(value, true, null, null, null);
        }else {
            putNode(root,value);
        }

    }
    
    private void putNode(RBNode node,int value){
        if(value < node.value){//1、比node小
            if(node.left == null){//1.1、 左孩子空，放入左孩子
                RBNode newNode = new RBNode(value, RED, node, null, null);
                node.left = newNode;
                return;
            }else {//1.2、 左孩子不为空，递归左孩子
                putNode(node.left,value);
            }
        }else {//2、比node大
            if(node.right == null){// 2.1、右孩子为空，放入右孩子
                RBNode newNode = new RBNode(value, RED, node, null, null);
                node.right = newNode;
                return;
            }else {//2.2 右孩子不为空，递归右孩子
                putNode(node.right,value);
            }
        }
    }

四、上面学会了，只能建立一个简单二叉树，不是平衡的，要想要树平衡，首先要学两个规则，左旋和右旋。

左旋：把一个节点看成一个三角形，左旋就是向左旋转(逆时针)，就是下图中 5 替代 2 的位置。

左旋官话：右节点替代根节点，根节点变为右节点的左节点，右节点的左节点变为根节点的右节点（绕的一比）。

左旋分两步：1、5替代2的位置(根节点2往左旋，右孩子5上位替代自己的位置)。

2、5的左孩子变为2的右孩子(2上位当老大，左孩子4不要，扔给退位的老大2来收养)。

注意：旋转是指根节点旋转，即主角是2，针对2来说的。

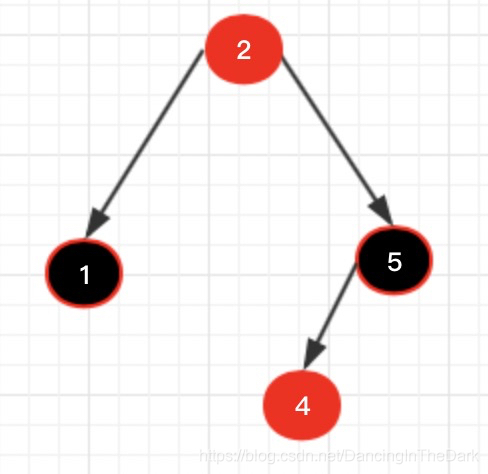左旋后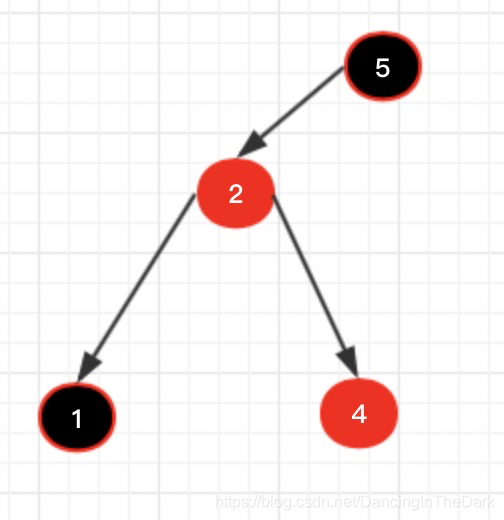

java代码实现：

public void leftRotate(RBNode p){
        if(p != null){
            RBNode r = p.right;
            p.right = r.left;
            if(r.left != null){
                r.left.farther = p;
            }
            r.farther = p.farther;
            if(p.farther == null){
                root = r;
            }else {
                if(p == leftOf(parentOf(p))){
                    leftOf(parentOf(p)).left = r ;
                }else {
                    rightOf(parentOf(p)).right = r;
                }
            }
            r.left = p;
            p.farther = r;
        }
    }

问题：1、如果右孩子为空怎么旋转呢？

答案：右孩子为空，不会触发右旋这个动作的，如果触发了，你代码有问题。

2、如果5没有左孩子怎么办呢？

答案：什么都不操作，不赋值了。

右旋：把一个节点看成三角形，右旋就是往右旋转(顺时针)，如下图节点 5 的右旋。

右旋官话：左节点替代根节点，根节点变为左节点的右节点，左节点的右节点变为根节点的左节点。（也是绕的一比）

右旋也是两步：1、根节点5往右旋，左孩子2上位替代自己的位置。
2、2的原右孩子4不要了，扔给5来收养，变为5的左孩子。

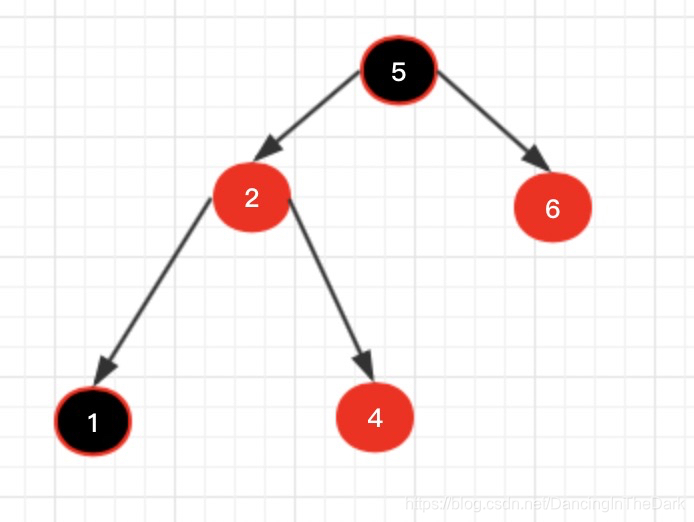右旋后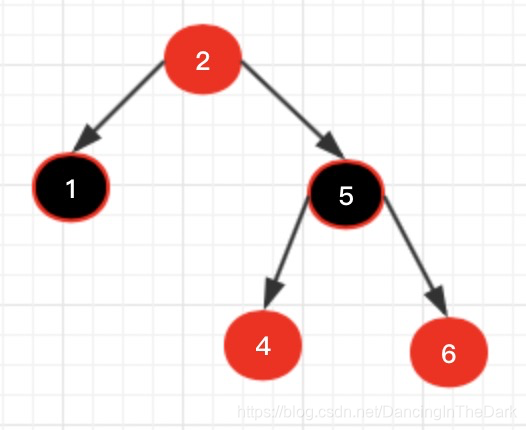

Java 代码实现：

public void rightRotate(RBNode y){
        if (y != null) {
         RBNode x = y.left;
         y.left = x.right;
         if(x.right != null){
             x.right.farther = y;
         }
         x.farther = y.farther;
         if(y.farther == null){
             root = x;
         }else {
             if(y == leftOf(parentOf(y))){
                 parentOf(y).left = x;
             }else {
                 parentOf(y).right = x;
             }
         }
         x.right = y;
         y.farther = x;
        }
    }

思考：左旋和右旋的结果是什么？为什么这样做？

右旋一般是树的左节点值太多，左边太重，需要把值往右边移动一点，像扁担一样，左边篮子太重，把货物往右移动一点，这样才能平衡，左旋也是同样的道理，这是红黑树平衡的主要操作。

五、明白的树的结构，我们来看下红黑树的规则，和博主的个人理解。

红黑树的规则：
     1、节点非黑即红。
   2、根节点是黑色。
   3、红节点的子节点必须是黑色。（不能出现连续的红色，可以连续的黑色）。
4、从根节点到叶子节点或者空叶子节点的每条路径，黑色节点数量相同。

潜规则：空节点都是黑色，新节点都是默认红色。

规则很抽象，我说下我对红黑树设计的理解，读者仅供参考。
1、节点非黑即红，为什么非黑即红？不能来个白色？
个人理解：树只要两个状态，平衡和非平衡，黑色表示“平衡”，表示当前节点很安全，红色表示“不平衡”，表示当前树很可能过重，需要调整，发出警告，所以出现连续的红红节点，往往树就开始进入了调整逻辑，红想象为重，黑想象为轻。

2、根节点是黑色，为什么根节点是黑色？红色不行么？
个人理解：主树必须是平衡的，根节点黑色，表示当前节点的树是平衡的，当依次插入2、1、3的时候，2是根节点黑色，1、3是子节点红色，很平衡。

3、红节点的子节点必须是黑色，为毛？
个人理解：红色已经表示可能偏重了，红红岂不是更重，红红需要调整，一般会把其中一个红节点调为平衡状态，变为安全的黑色。

4、黑色节点数量相同。

个人理解：节点相同说明树是平衡的，根节点查找的时间复杂度也平衡。

六、说下树的调整思路：由小到大调整，平衡的小树视为一个整体。

为了理解，我引入几个通俗概念：小树：爷爷节点的所有子节点。大树：整颗树。父节点：当前节点的上级节点。叔叔节点：爷爷节点非父节点。

最关键的问题来了，什么时候应该矫正？应该怎么矫正？

什么时候矫正？

1、新插入的节点必须为红色。（因为这个小秤砣加入可能会破坏树的平衡）

2、如果发现父亲也是红色，立刻进入平衡修正处理。（父亲已经红了，自己再加入，明显偏重）

怎么矫正？

还是那个思想，一棵树一棵树的调整，小树平衡了，把小树看成一个节点，调整小树所在的小树，直到根节点平衡。

新节点是红色，连续的红色表示小树的父亲分支可能过重，这时候要看叔叔是不是很轻松（叔叔是不是黑色），叔叔有两种颜色。

1、如果叔叔是红色，说明叔叔也是压力山大，不能帮父亲分担了，说明父亲和叔叔已经无法平衡了，所以父亲叔叔全部涂成黑色，把爷爷涂红，爷爷开始报警（爷爷的父节点可能偏重），处理爷爷，这时候思想要转变，把爷爷这颗小树看成一新节点，重新进入平衡程序。

2、如果叔叔是黑色（空节点也是黑色哦），说明叔叔很轻松嘛，想办法分给叔叔一点。这要分细点，情况要考虑周全，不然分不均。

情况有四种：父亲是左节点或者是右节点，自己是左节点或者右节点，相乘得4种情况。

1、父亲是左节点，自己是右。
2、父亲是左节点，自己是左。

3、父亲是右节点，自己是左。

4、父亲是右节点，自己是右。

情况1：父亲是左节点，自己是右。如图所示。新插入14，父亲13 是爷爷15 的左节点，是左爸爸，自己是爸爸的右节点，是右儿子（不像亲生的）

处理：1、左旋父亲13，自己14替代父亲13的位置（因为14离15很近，更适合当15的节点），

2、再把14涂黑。（表示我14平衡了）
3、把爷爷15涂红。（爷爷可能不平衡）
4、右旋爷爷15。

结果如下：

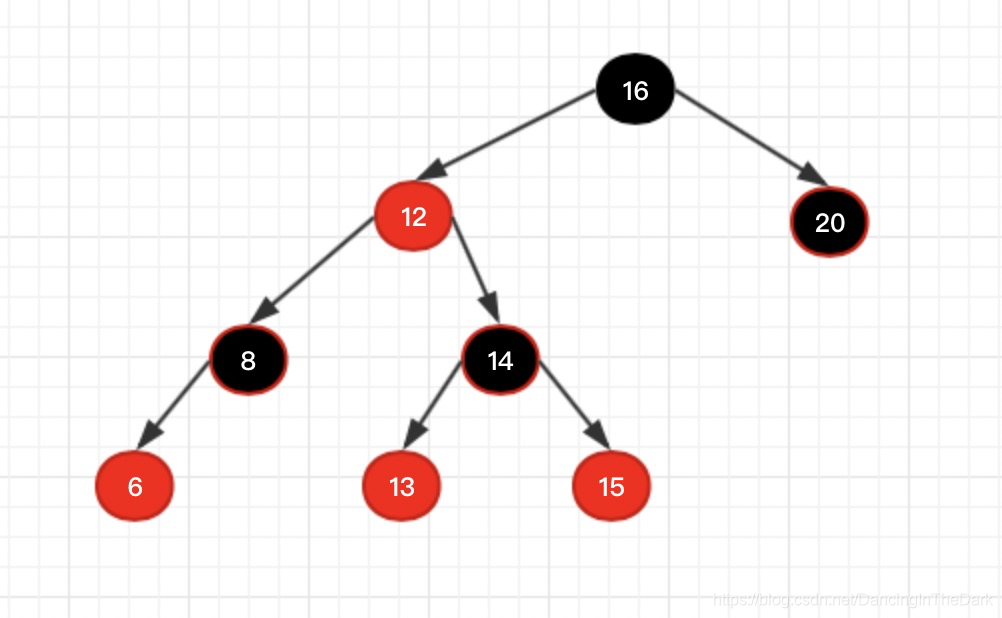
这个新加的右儿子很厉害，干掉了爸爸，又干掉了爷爷，左脚踩着爸爸，右脚踩着爷爷。

情况2：父亲是左节点，自己是左。如下图所示：父亲14是爷爷15的左节点，自己13是爸爸14的左节点。

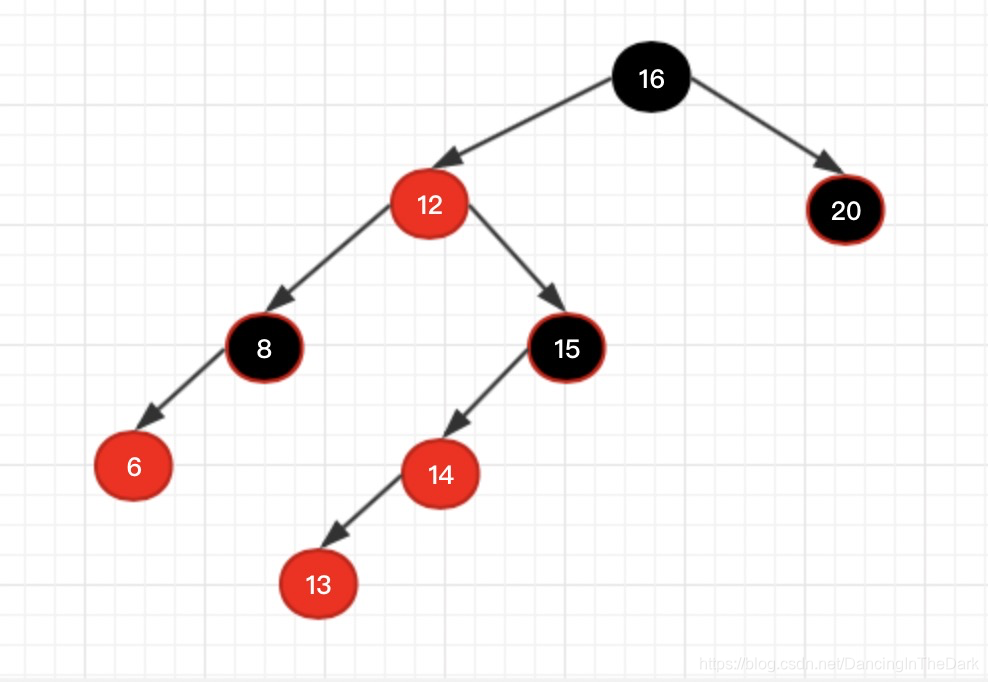
处理：1、父亲14涂黑，爷爷15涂红，右旋爷爷（爸爸上位）。

结果如下：

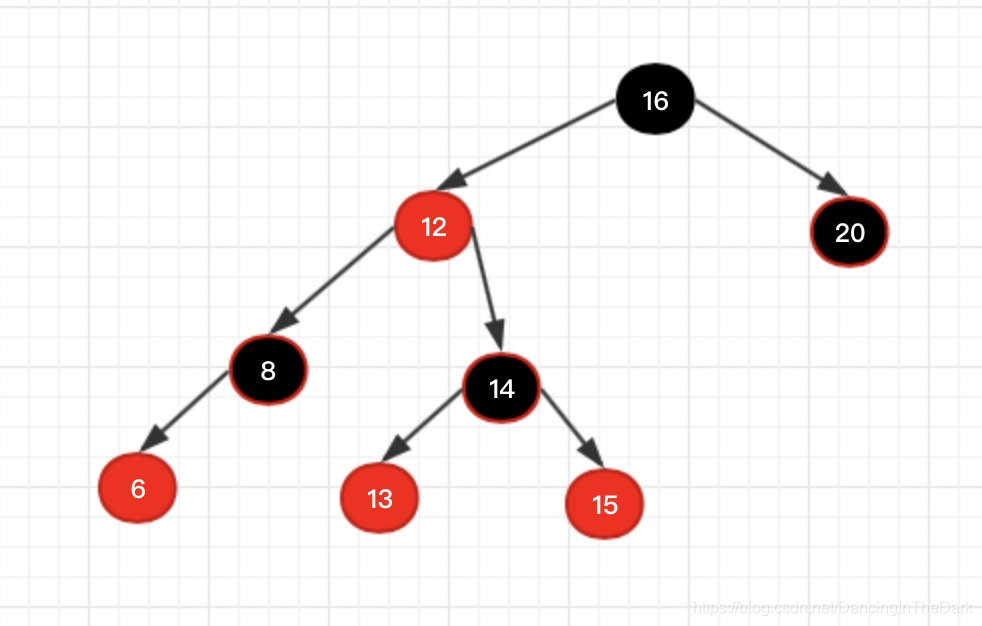
心细的同学可能会发现，结果跟情况1一样，目的都是让14上位，树才平衡。

情况3：父亲是右节点，自己是左。如图，新节点29是左节点，父节点30是右节点。

解决：父节点30右旋(29替代30的位置)，再把29涂黑，28涂红，左旋28。(目的很明显，29替代原28的位置)

结果如下：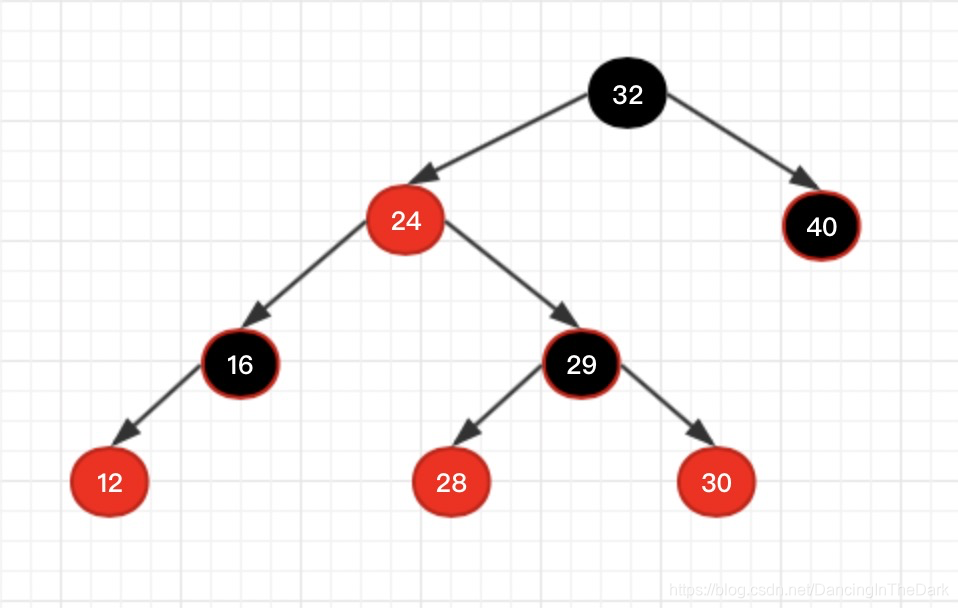

情况4：父亲是右节点，自己是右。如下图，新节点30是右节点，父节点29是右节点。

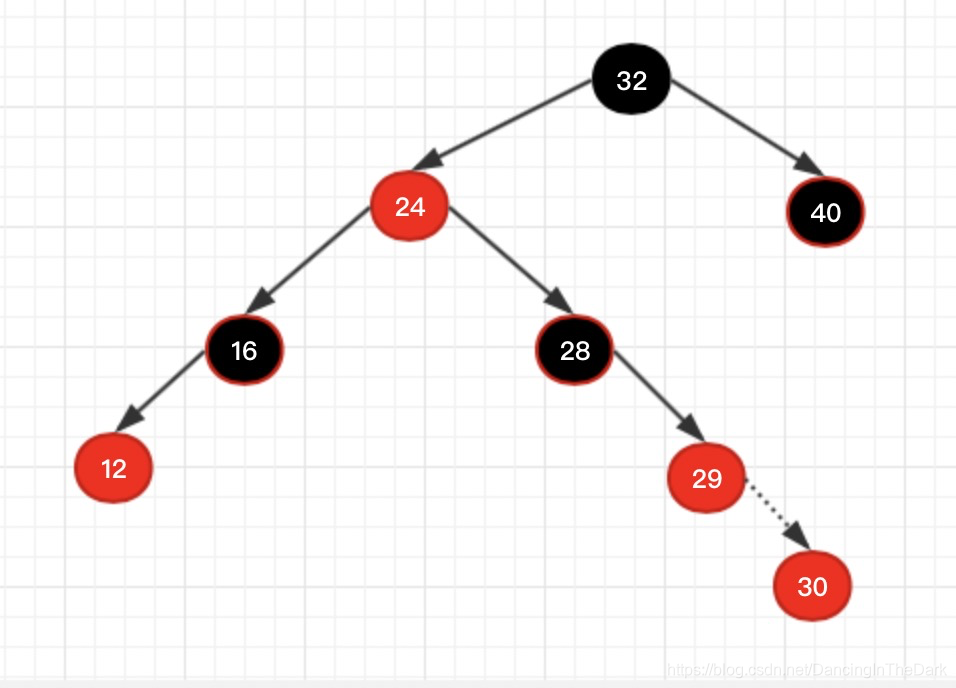
解决：父节点29涂黑，爷爷28涂红，左旋爷爷28，（父亲上位替代爷爷）结果如下：

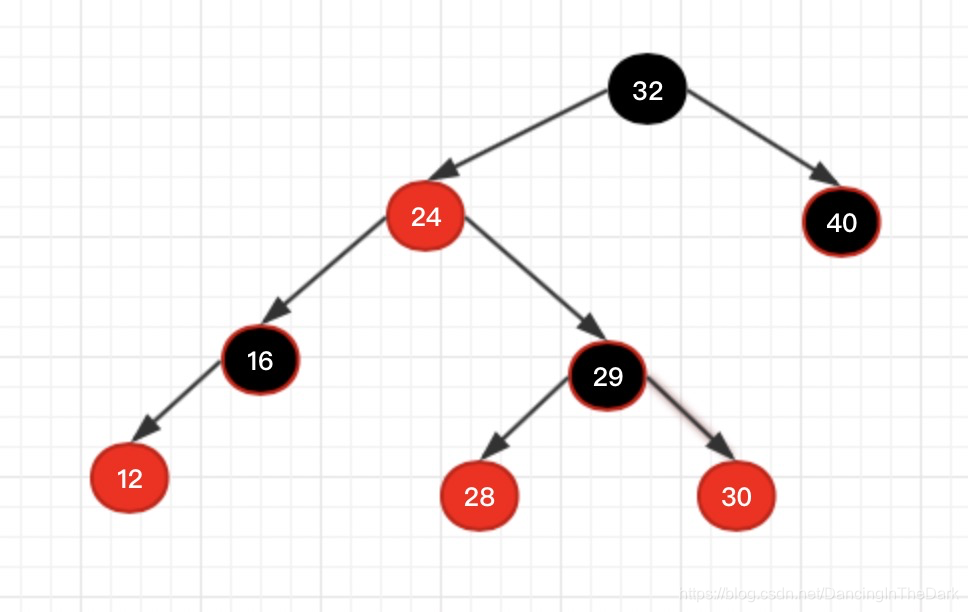
以上4种情况，便是红黑树自平衡的主要逻辑，其中涉及到变色和旋转，以这样做的目的和原因。

总结在一起如下：

前提：x节点的父节点是红色
        一、x的父节点是左节点
           1、x的叔叔是红色
              解决：x的父亲涂黑，叔叔涂黑，爷爷设置为红色，处理爷爷
           2、x的叔叔是黑色
              解决：1、x是右节点
                      x设置为父节点，左旋x，x的父亲设置为黑、x的爷爷设置为红，右旋x的爷爷
                   2、x是左节点
                      x的父亲设置为黑，x的爷爷设置为红，右旋x的爷爷
        二、x的父节点是右节点
           1、x的叔叔是红色
              解决：父亲涂黑、叔叔涂黑、爷爷设置为红色，处理爷爷（叔叔红了，没办法分，压力交给爷爷）
           2、x的叔叔是黑色
              解决：1、x是左节点
                      x设置为父节点，右旋x(x变换到右下角)，x的父亲设置为黑，x的爷爷设置为红，左旋x的爷爷（新增的值小于父亲，大于爷爷，应该作为支撑点）
                   2、x是右节点
                      x的父亲设置为黑，x的爷爷设置为红，左旋x的爷爷 （父亲+我太重，父亲上位，分给那边一个）

        总结：小树（爷爷以下）不平调小树，小树平了调大树
             1、只要父亲叔叔是红色，全部涂黑，爷爷涂红，问题抛给爷爷，处理爷爷（目前小树平衡，大树可能不平衡，需要调整大树）
             2、叔叔是黑色，爷爷小树不平衡（父亲偏重），如果当前节点跟父亲左右不一致，则旋转父节点变为一致，之后再旋转爷爷（分给叔叔），结束

java代码实现如下：

private void fixNode(RBNode x){
        x.color = RED;

        while (x != null && x != root && isRED(parentOf(root))){
            if(parentOf(x) == leftOf(parentOf(parentOf(x)))){
                RBNode uy = rightOf(grandpa(x));
                if(isRED(uy)){
                    setBalck(parentOf(x));
                    setBalck(uy);
                    setRed(grandpa(x));
                    x = grandpa(x);
                }else {
                    if(x == rightOf(parentOf(x))){
                        x = parentOf(x);
                        leftRotate(x);
                    }
                    setBalck(parentOf(x));
                    setRed(grandpa(x));
                    rightRotate(grandpa(x));
                }
            }else {
                RBNode uy = leftOf(grandpa(x));
                if(isRED(uy)){
                    setBalck(parentOf(x));
                    setBalck(uy);
                    setRed(grandpa(x));
                    x = grandpa(x);
                }else {
                    if(x == leftOf(parentOf(x))){
                        x = parentOf(x);
                        rightRotate(x);
                    }
                    setBalck(parentOf(x));
                    setRed(grandpa(x));
                    leftRotate(grandpa(x));
                }
            }
        }
        this.root.color = BLACK;
    }

    private void setRed(RBNode node){
        if(node != null){
            node.color = RED;
        }
    }
    private void setBalck(RBNode node){
        if(node != null){
            node.color = BLACK;
        }
    }
    private RBNode parentOf(RBNode node){
        return node == null ? null : node.farther;
    }
    private RBNode leftOf(RBNode node){
        return node == null ? null : node.left;
    }
    private RBNode rightOf(RBNode node){
        return node == null ? null : node.right;
    }
    private RBNode grandpa(RBNode node){
        return parentOf(parentOf(node));
    }
    private boolean isRED(RBNode rbNode){
        return rbNode == null? false : (rbNode.color == RED);
    }

博主的思路终结一下：

总结：小树（爷爷以下）不平调小树，小树平了调大树
     1、只要父亲叔叔是红色，全部涂黑，爷爷涂红，问题抛给爷爷，处理爷爷（目前小树平衡，大树可能不平衡，需要调整大树）
     2、叔叔是黑色，爷爷小树不平衡（父亲偏重），如果当前节点跟父亲左右不一致，则旋转父节点变为一致，之后再旋转爷爷（分给叔叔），结束

以上便是红黑树的插入逻辑部分，设计的变色和旋转，树的查找很low，此处不做解析，树的删除有点麻烦，以后有空再解析。