谁说前端不能搞红黑树，用这55张图拿JS一起手撕红黑树

Hi~，我是一碗周，如果写的文章有幸可以得到你的青睐，万分有幸~

🍎 写在前面

红黑树是数据结构与算法中比较难理解的一个树状结构了，在前端开发中，如果仅仅是业务开发的话，几乎是用不到红黑树的；那为什么还有学习红黑树呢？红黑树可以说是现在应用的最复杂的二叉树之一，如果红黑树都能掌握还会怕其他的树状结构嘛？

通过本篇文章你将会掌握下面这些内容，我大概说明了内容以及难度：

上面的难度划分仅仅是我按照文中的内容进行划分，如果大佬非说红黑树的操作简单，大佬，请收下我的膝盖。

🥭 平衡树和不平衡树

二叉搜索树又分为平衡树和不平衡树，如下图所示：

上图的两棵树都是二叉搜索树，左边这颗平衡的二叉搜索树查找一个节点的时间复杂度是，假如有10个亿的数据只需要查找30次即可；右边这颗不平衡的二叉搜索树就相当于是一个排序后的链表，时间复杂度最坏为，假如还是10亿数据，查找可能需要10亿次。

假如我们依次往二叉搜索树插入1, 2, 3, 4, 5, ... n，插入的数量为n，树的高度也是n，因为我们最新插入的节点永远都是叶子节点。

常见的平衡树主要有AVL树和红黑树：

• AVL树的出现早于红黑树的，它是一颗高度平衡树，它的任意节点的左右子树的高度差不会超过1，每为其增加一个节点，如果其左右子树的高度差超过了1，都会进行旋转，直到平衡为止；由于其需要频繁进行旋转，所以其性能要低于红黑树。
• 红黑树通过变色、左旋、右旋来保持二叉搜索树的平衡性（这里的平衡性指的是黑色平衡，所谓的黑色平衡就是每个节点到叶子节点所经过的黑色节点是一致的），性能要优于AVL树，所以现在平衡树的应用都是红黑树。

🍏 AVL树

AVL树并不是这篇文章的重点，这里仅仅介绍一个AVL树的构建过程，从而说明为什么红黑树的性能要优于AVL树。

假如我们往二叉搜索树中依次插入10, 9 ,8, 7, 6, 5, 4, 3, 2, 1，二叉搜索树是下面这个样子的：

根据这个图我们可以看出这棵二叉树已经退化成了一个有序链表，现在我们用AVL树来优化一下。

第一步：插入10和9，这个没有什么可说的直接插入就好；

第二步，插入8，发现10的左子树的高度为2，右子树的高度为0，需要进行旋转，如下图：

第三步：插入数据7，插入后任意一个节点都满足左右子树的高度差不大于1，所以不用进行旋转。

第四步：插入数据6，插入后发现节点8和节点9的左右子树高度差都是大于1的，需要进行旋转，当出现多个节点不满足左右子树高度差都是大于1时，旋转距离插入节点最近的祖先节点 ，如下图所示：

第五步：插入数据5后，对于根节点9来说，左子树的高度为3，右子树的高度为1，需要进行旋转，过程如下：

第六步，插入数据4，对于节点6来说，左子树的高度为2，右子树的高度为0，需要进行旋转，过程如下：

第七步：插入数据3，插入后插入后任意一个节点都满足左右子树的高度差不大于1，所以不用进行旋转。

第八步：插入数据2，对于节点4来说，左子树的高度为2，右子树的高度为0，需要进行旋转，过程如下：

最后一步，插入数据1，插入数据1后需要

AVL树为每个节点都维护一个平衡因子，平衡因子的值是左子树的高度减去右子树的高度或者右子树的高度减去左子树的高度；当节点的平衡因子的值为1、0、-1，则说明它是平衡的，当节点的平衡因子的绝对值大于2时，则说明这棵树是不平衡的，需要进行旋转。

上图出自为维基百科

🍑 AVL树和红黑树优缺点对比

首先我们先来看一下如果上面那些数据依次插入红黑树是什么样子的，先不用管红黑树是怎么构建的，这里主要分析一下AVL树和红黑树的优缺点。

从上图中我们可以看到：

• 红黑树并没有追求完全平衡，它只是黑色节点平衡（即根节点到叶子节点的黑色节点数量一致，例如节点5到任何叶子节点的黑色节点数量都是2），而AVL树是高度平衡树，也就是追求完全平衡；这就意味这AVL树随着节点数量的越来越多，出现不平衡时，旋转次数也就会也来越多，而红黑树出现任何不平衡，旋转三次之内一定会解决（后面会验证这个结论）
• 删除一个树种的节点导致失衡，AVL树需要从维护从根节点到删除节点路径上所有节点的平衡，时间时间复杂度时为O(logn)，而红黑树最多只需旋转三次即可恢复平衡，时间复杂度为O(1)；
• 由于AVL树是高度平衡树，查找效率要高于红黑树，但是红黑树比AVL树不平衡最多一层，也就是说差多最多就差一次。

基于以上几点得出红黑树的综合能力要优于AVL树，表现会更加稳定。

🍒2-3-4树

2-3-4树是四阶的B树，它属于一种多路查找，其具有以下限制：

B树是一种自平衡的树，其插入、查找和删除的时间复杂度都是O(logn)

• 所有叶子节点都必须具有相同的深度，也就说2-3-4树是一颗满树；

• 2-3-4树把数据存储在元素中，元素组成节点，节点只能是下列之一

  • 2-节点：包含一个元素和2个子节点；
  • 3-节点：包含两个元素和3个子节点；
  • 4-节点：包含三个元素和4个子节点。

• 元素使用保持排序顺序，整体上保持二叉搜索树的特质，即左子树小于根节点，右子树大于跟节点；

2-3-4树的节点如下所示：

🍓2-3-4树的构建过程

现在我们从头来构建一颗2-3-4树，往树中依次插入71, 88, 80, 90, 89, 91, 66, 101, 150, 130, 166：

第一步：由于2-3-4树必须是满树，且可以是2~4节点，所以前三个元素直接构成一个4节点：

第二步：插入元素90，过程如下图：

第三步：插入元素89，合并节点后插入元素91，过程如下：

第四步：插入元素66，过程如下：

第五步：插入元素101，过程如下：

第六步：插入元素150，过程如下：

第七步：插入元素166合并节点后，插入元素130，过程如下：

此时如果我们在插入一个元素，他会寻找自己的位置，并于原节点组成新的节点，例如插入元素35，最终的2-3-4树如下所示：

由构建过程可以得知，2-3-4的构建是从叶子节点依次到根节点进行构建。

🫐 2-3-4树与红黑树的关系

2-3-4树的任意一个节点，都至少对应红黑树的一种结构，也就是说2-3-4树至少对应一棵红黑树，一棵红黑树对应一颗2-3-4树，如下图展示了2-3-4树中的节点与红黑树结构的对应关系

2-3-4树还有一个状态，就是一个4节点插入元素后，这里将这个状态称为裂变状态，如下图所示：

根据新插入元素的大小不同分为不同的4个位置。

🍈 2-3-4树与红黑树的转换

我们了解了2-3-4树与红黑树的关系后，现在我们将之前画的2-3-4树转换为红黑树，如下图所示：

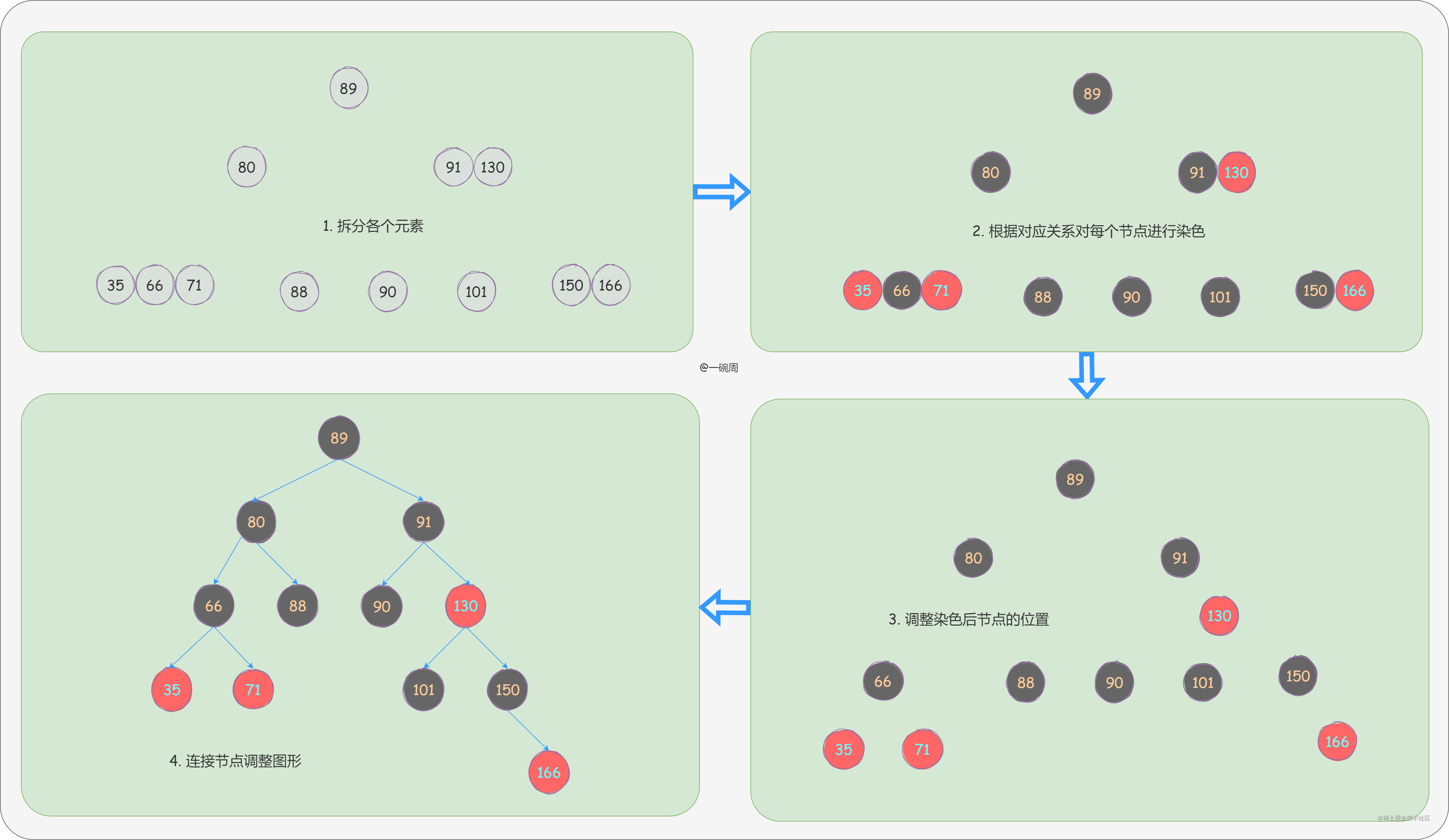
现在来将一颗红黑树转换为2-3-4树，如下图所示：

🍊 红黑树

前面我们用了很大的篇幅来介绍平衡的二叉搜索树、AVL树和2-3-4树，其目的就是为了更好更快的学习和了解红黑树，现在我们正式开始进入红黑树的学习。

🍉 红黑树的五大特性

红黑树除了满足二叉搜索树的基本规则外，还满足以下五个特性：

• 节点是红色或者黑色（废话，要不然咋叫红黑树）；

• 根节点是黑色（这是因为红黑树是由2-3-4树转换而来，根据2-3-4树的2节点、3节点或者4节点转换为红黑树的结对应关系，黑色节点总是作为父节点）

• 每个叶子节点都是黑色的空节点（这里的叶子节点指的NIL节点，如下图）

  

• 每个红色节点的两个子节点都是黑色，也就是说叶子节点到根节点所在的路径上不会出现两个连续的红色节点。

  出现红色节点的情况主要有两种情况：

  • 2-3-4树的3节点会出现一个红色节点；
  • 2-3-4树的4节点会出现两个红色节点；

  2-3-4树的3节点肯定会出现3个节点，这三个节点不管是什么节点都存在黑色节点，最小的那个黑色节点作为红色节点父级的左子树，剩余的两个节点作为红色节点的左右子树，如下图所示：

  

  2-3-4树的4节点的情况与3节点类似，如下图所示：

  

• 从任意节点到其他叶子节点的所有路径所包含相同数量的黑色节点；这是因为2-3-4是一颗满树，每个节点转换为红黑树只有一个黑节点。

🍒 完整代码

红黑树的源代码在GitHub中，各位看官可以结合源代码与文本一起食用，效果更佳。

🍋 红黑树的变色操作

本篇文章中关于红黑树的操作全部使用JavaScript完成，首先我们定义一个类，用于创建红黑树的节点，然后在定义一个类，用于实例化红黑树，代码如下：

const RED = 'RED'
const BLACK = 'BLACK'
class RBNode {
   
  /**
   * 创建一个新的节点
   * @author ywanzhou
   * @param {number} val 要插入的数值
   * @param {RBNode} parent 父节点
   * @param {RBNode} left 左子树
   * @param {RBNode} right 右子树
   * @param {string} color 颜色
   * @returns 一个新的节点
   */
  constructor(val, parent, left = null, right = null, color = RED) {
   
    if (color !== RED && color !== BLACK)
      throw new Error('color can only be RED or BLACK')
    this.val = val
    this.parent = parent
    this.left = left
    this.right = right
    this.color = color
  }
}
class RBTree {
   
  constructor() {
   
    this.root = null
  }
}

节点的变色操作比较简单，无非就是黑色变红色，红色变黑色，示例代码如下：

/**
 * 给定一个节点，修改节点的颜色 这是一个私有方法
 * @author ywanzhou
 * @param {RBNode} node 需要改变的颜色
 * @param {string} color 需要节点改变后的颜色
 */
#setColor(node, color) {
   
  if (color !== RED && color !== BLACK)
    throw new Error('color can only be RED or BLACK')
  if (!node) throw new Error('node is a empty RBNode')
  node.color = color
}

🍌 红黑树的旋转操作

旋转操作分为左旋和右旋，我们依次来看：

• 左旋转：又称逆时针旋转，旋转时以某个节点作为旋转点，其右子节点变成自己的父节点，右子节点的左节点变成旋转节点的右节点，过程如下图所示：
  

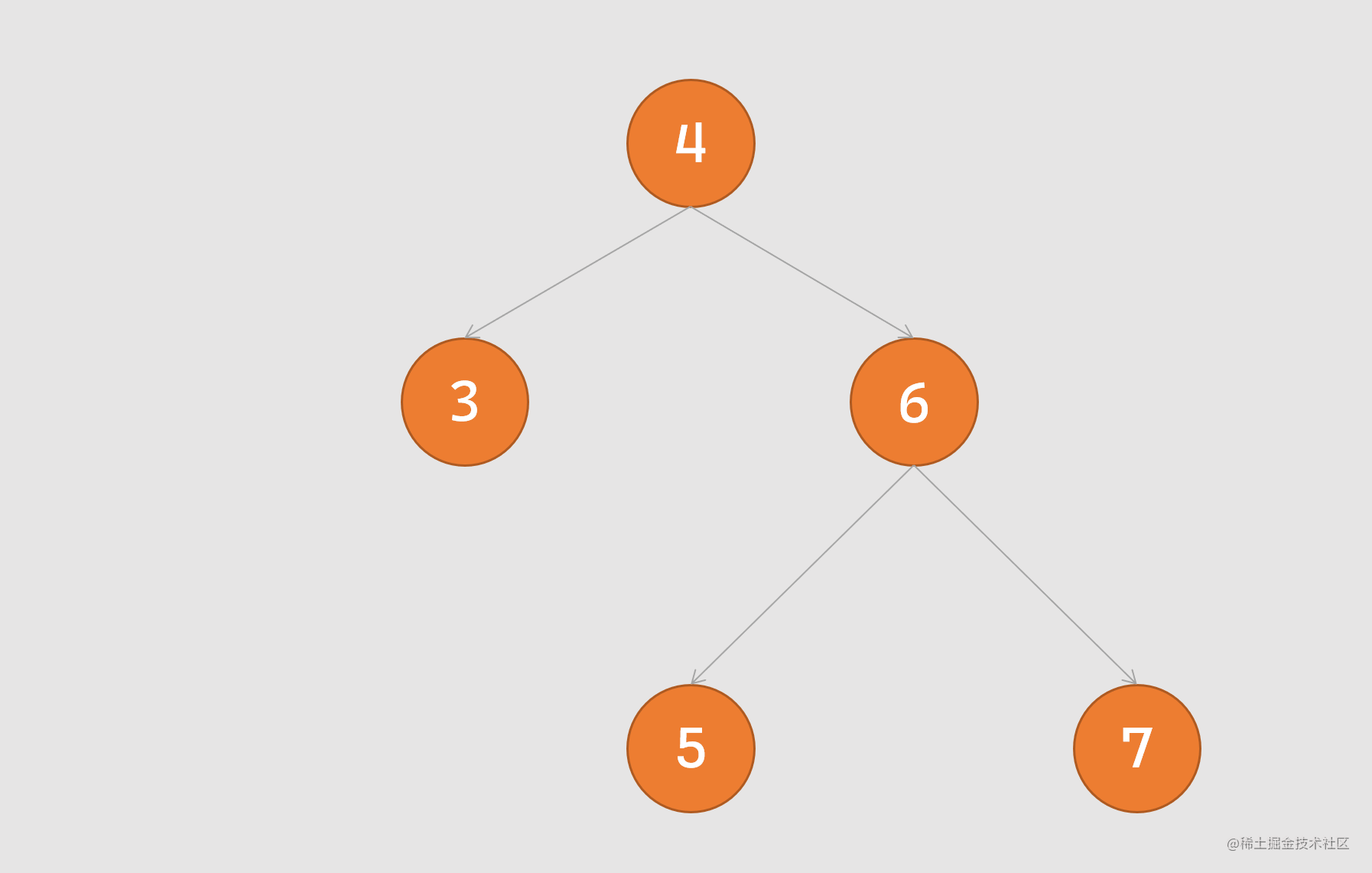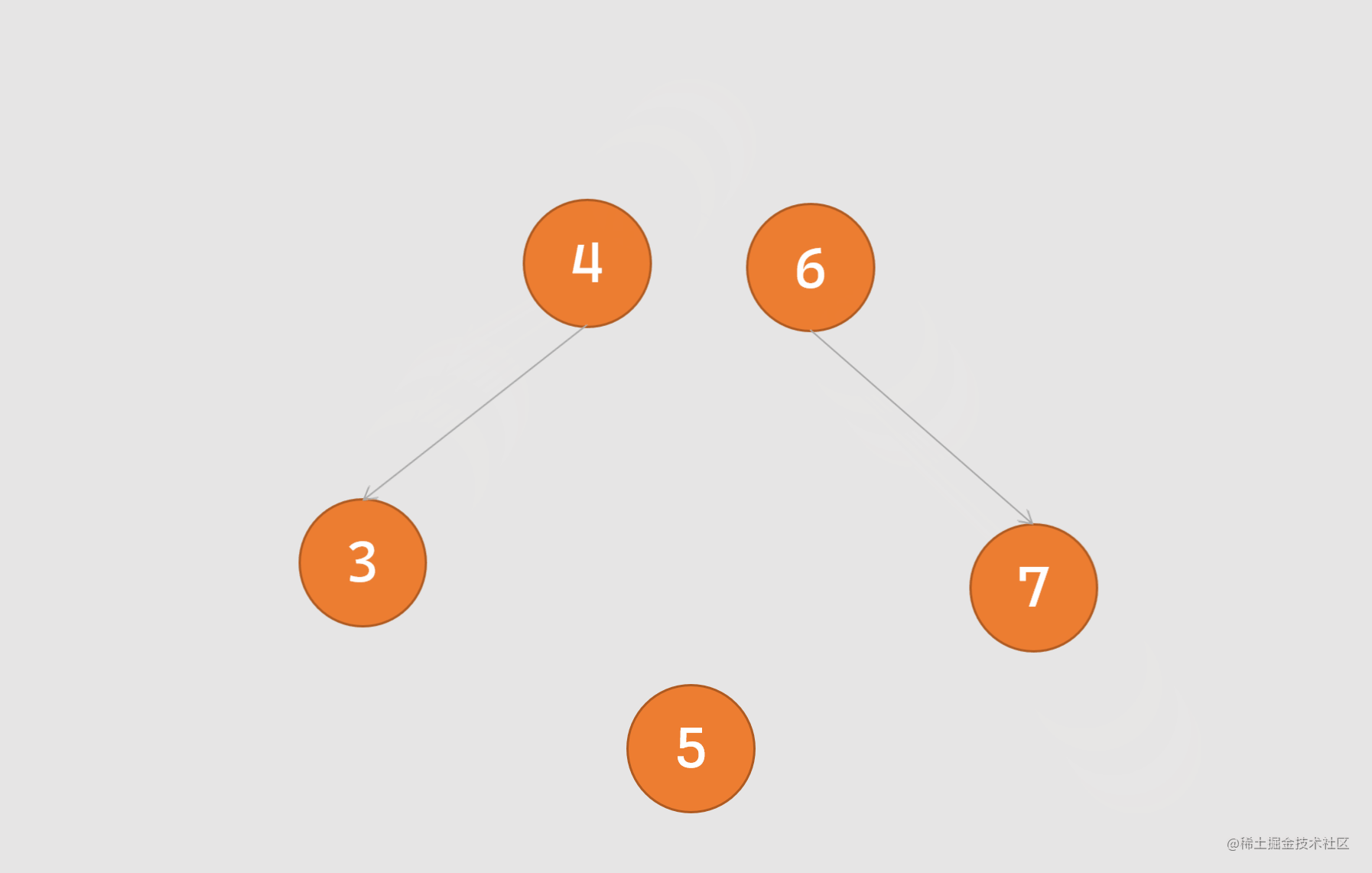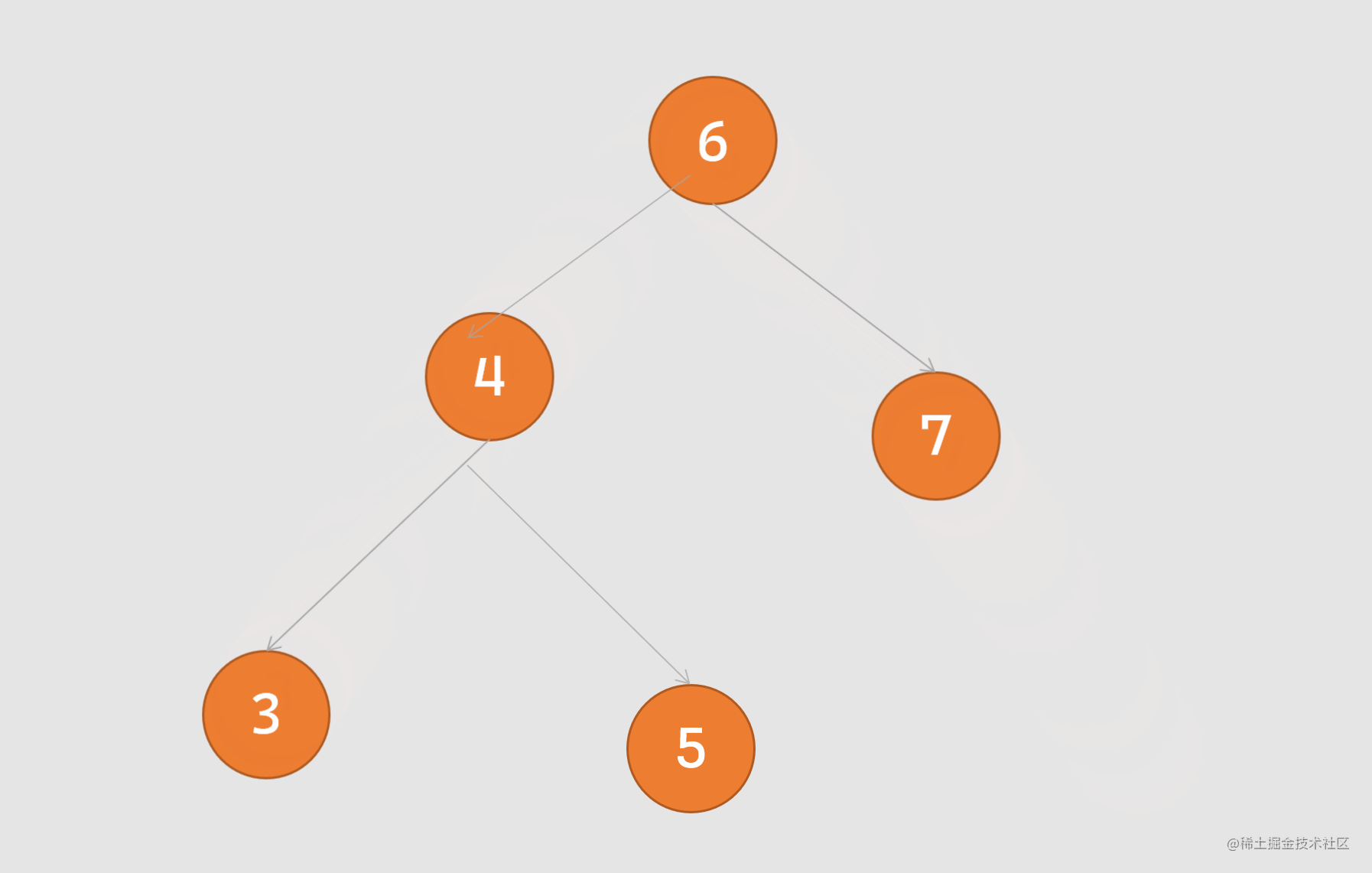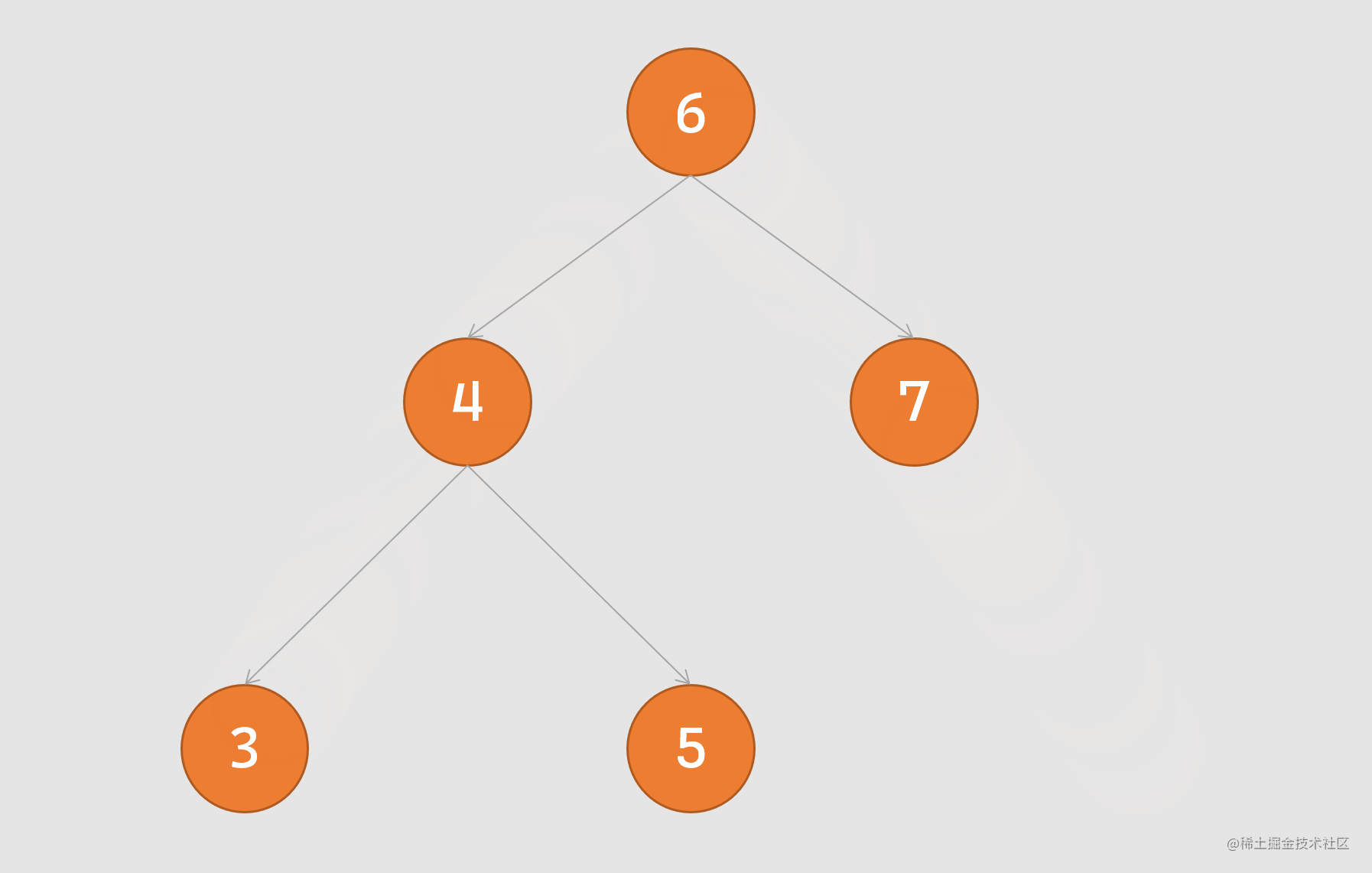
• 右旋转：又称顺时针旋转，旋转时以某个节点作为旋转点，其左子节点变成自己的父节点，左子节点的右节点变成旋转节点的左节点，过程如下图所示：
  

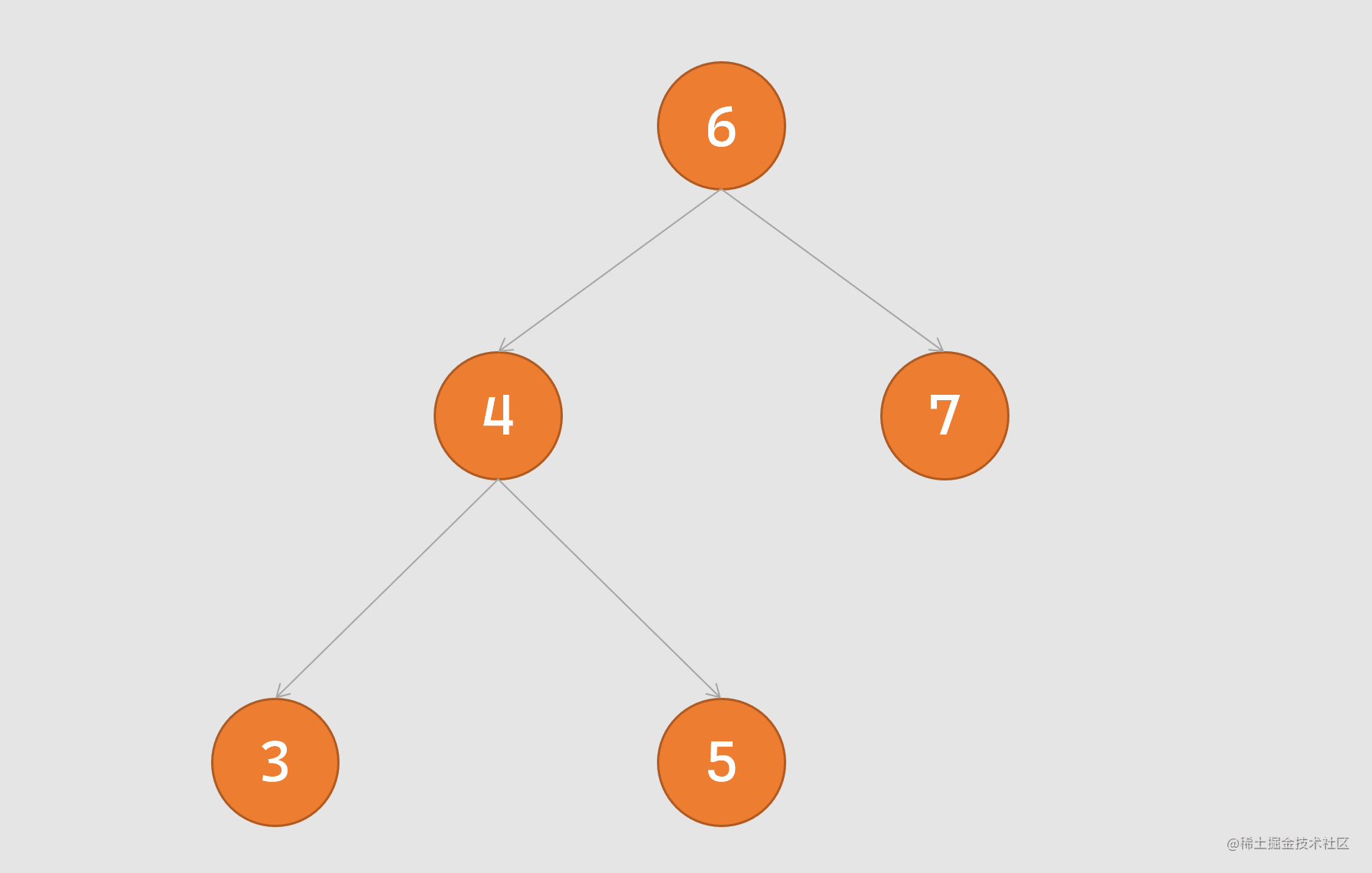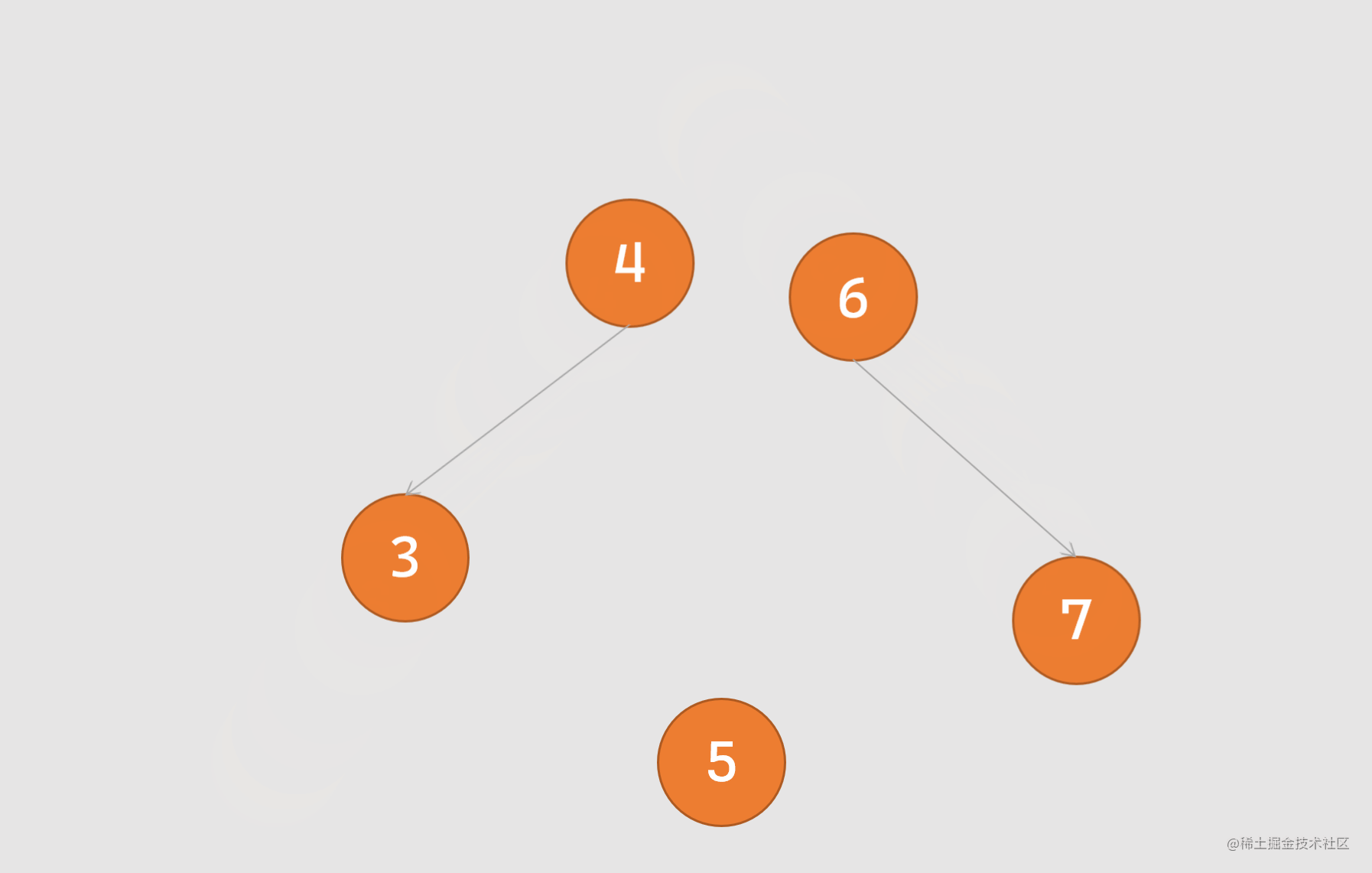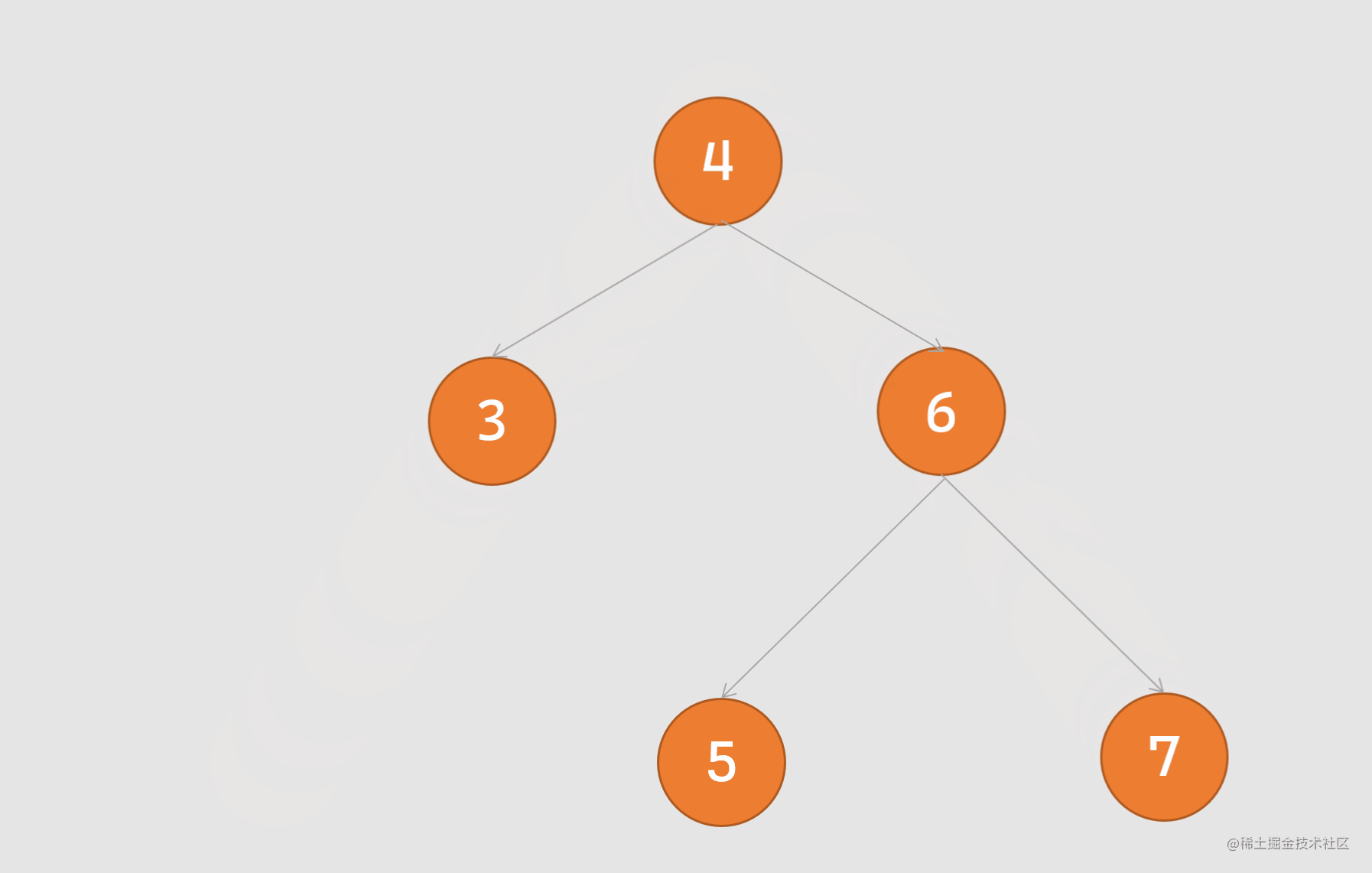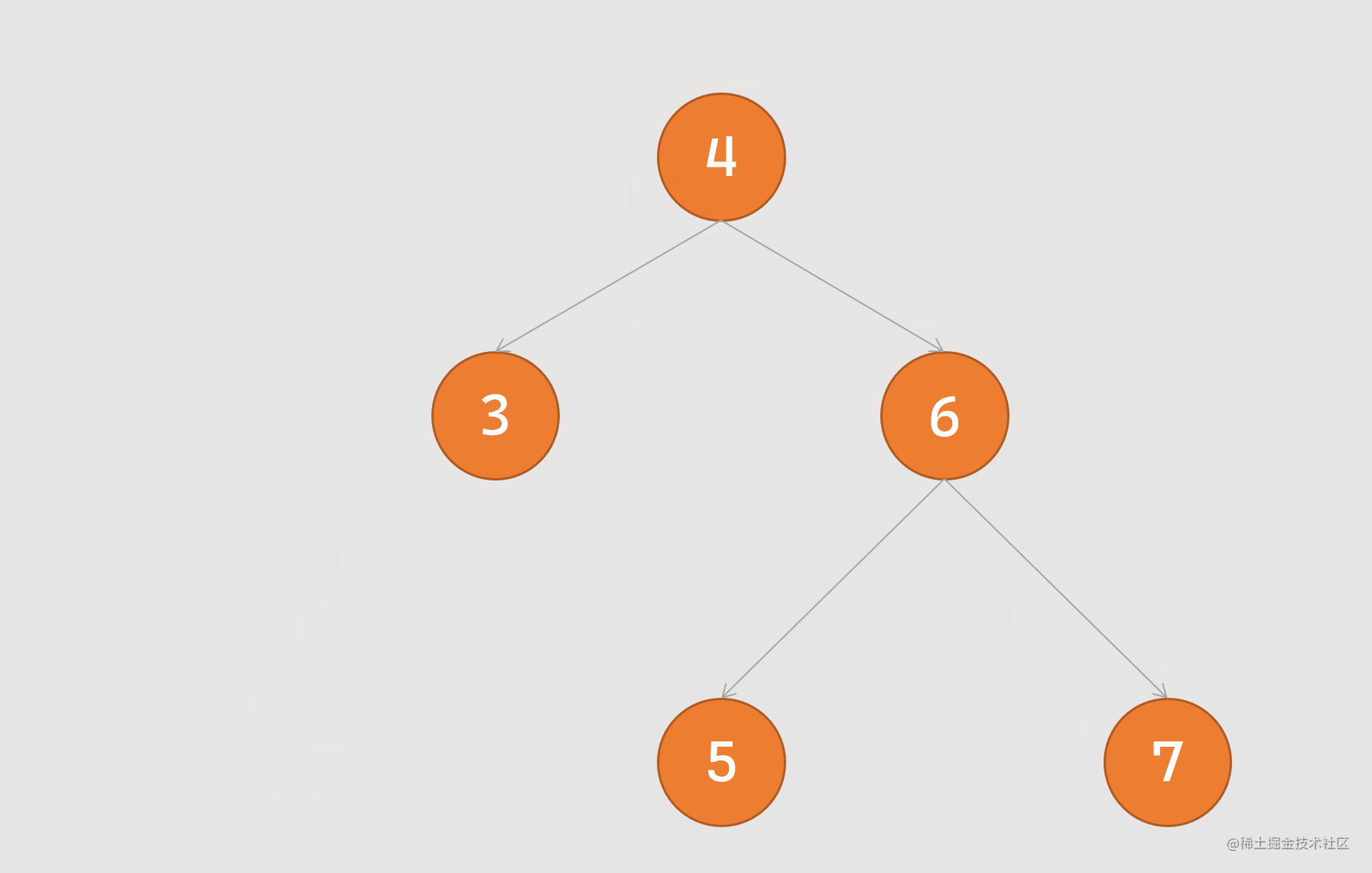
实现左旋右旋的代码如下 （下列的代码中每一行均有注释，两种旋转方式一种是对代码的理解，一种是实现步骤）：

/**
 * 围绕 node 进行左旋
 * 效果如下
 *         node           ->          pr(r)
 *        /   \           ->         /   \
 *       pl   pr(r)       ->       node   cr
 *           / \          ->       /  \
 *          cl  cr        ->      pl   cl
 * @author ywanzhou
 * @param {Node} node 需要旋转的节点
 */
#leftRotate(node) {
   
  if (!node) return
  // 缓存一下 node 的右节点
  const r = node.right
  // 将 pr 的右节点 pr 重新赋值为 cl
  node.right = r.left
  if (r.left !== null) {
   
    // 将 cl 的父节点指向 node
    r.left.parent = node
  }
  // 将节点r连接node节点的父节点
  r.parent = node.parent
  if (node.parent === null) {
   
    // 如果需要旋转的节点是根节点，则将根节点从node修改为r
    this.root = r
  } else if (node.parent.left === node) {
   
    // 说明要旋转的node是父节点的左节点
    node