python数据结构与算法学习之算法分析

算法分析

大O表示法

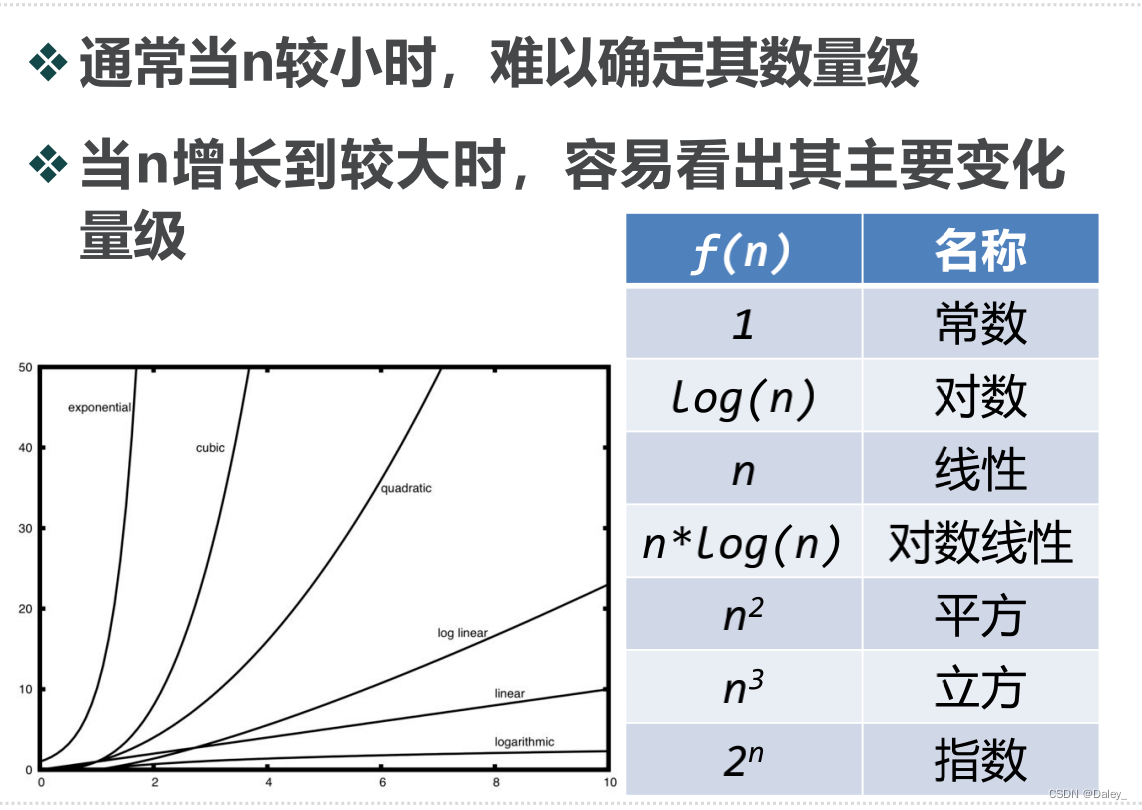
数量级函数 Order of Magnitude

1. 基本操作数量函数T(n)的精确值并不是特别重要，重要的是T(n)中起决定性因素的主导部分
2. 用动态的眼光看，就是当问题规模增大的时候，T(n)中的一些部分会盖过其它部分的贡献

“大O”表示法

数量级函数描述了T(n)中随着n增加而增加速度最快的主导部分，称作“大O”表示法，记作O(f(n))，其中f(n)表示T(n)中的主导部分

例子：T(n)=5n^2+27n+1005
当n很小时，常数1005其决定性作用
但当n越来越大，n^2项就越来越重要，其它两项
对结果的影响则越来越小
同样，n^2项中的系数5，对于n ^2的增长速度来说
也影响不大
所以可以在数量级中去掉27n+1005，以及系数5
的部分，确定为O(n^2)

常见的大O数量级函数

“变位词”判断问题

所谓“变位词”是指两个词之间存在组成字母的重新排列关系,如：heart和earth，python和typhon
为了简单起见，假设参与判断的两个词仅由小写字母构成，而且长度相等
可以很好展示同一问题的不同数量级算法

解法1:逐字检查

解法思路
将词1中的字符逐个到词2中检查是否存在，存在就“打勾”标记（防止重复检查；如果每个字符都能找到，则两个词是变位词，只要有1个字符找不到，就不是变位词。
将词2的对应字符设为None，以此来实现打勾标记。

#逐字检查法

def anagram_solution1(s1, s2):
    alist = list(s2)  # 将s2转换为字符串形式，方便其实现打勾操作
    pos1 = 0
    still_ok = True
    while pos1 < len(s1) and still_ok:  # 循环s1的每个字符
        pos2 = 0
        found = False
        while pos2 < len(alist) and not found:  # 在s2中逐个对比
            if s1[pos1] == alist[pos2]:
                found = True
            else:
                pos2 += 1
        if found:
            alist[pos2] = None  # 找到就打勾
        else:
            still_ok = False  # 1个字符找不到就为失败
        pos1 += 1
    return still_ok


print(anagram_solution1('python', 'typhon'))

主要部分为两重循环部分：
外层循环遍历s1的每个字符，内层循环执行n次，而内层循环在s2中查找字符，每个字符的对比次数，分别是1至n中的一个，而且各不相同
执行总次数： 1 + 2 + 3 + . . . + n
根据等差数列求和公式可知其数量级为
O($n^2$)

解法2: 排序比较

解题思路
将两个字符串都按照字母顺序排好序，再逐个字符对比是否相同，如果相同则是变位词，有任何不同就不是变位词。

# 排序比较法

def anagram_solution2(s1, s2):
    list1 = list(s1)
    list2 = list(s2)
    list1.sort() # 转为列表后再能排序
    list2.sort()
    pos = 0
    matches = True
    while pos < len(s1) and matches:
        if list1[pos] == list2[pos]:  # 若相同位置上元素相同，则检查下一个位置
            pos += 1
        else:
            matches = False  # 若不同，则返回错误
    return matches

print(anagram_solution2('python', 'typhon'))

粗看上去，本算法只有一个循环，最多执行n次，数量级是O(n)，但循环前面的两个sort并不是无代价的
如果查询下后面的章节，会发现排序算法采用不同的解决方案，其运行时间数量级差不多是O(n2)或者O(n log n)，大过循环的O(n)
所以本算法时间主导的步骤是排序步骤
本算法的运行时间数量级就等于排序过程的数量级O(n*log n)

解法3:暴力法

暴力法解题思路为：穷尽所有可能组合
将s1中出现的字符进行全排列，再查看s2是否出现在全排列列表中。
这里最大困难是产生s1所有字符的全排列，根据组合数学的结论，如果n个字符进行全排列，其所有可能的字符串个数为n!。
我们已知 n! 的增长速度甚至超过2n，暴力法太暴力！不好用！

解法4:计数比较

解题思路：对比两个词中每个字母出现的次数，如果26个字母出现的次数都相同的 话，这两个字符串就一定是变位词
具体做法：为每个词设置一个26位的计数器，先检查每个词，在计数器中设定好每个字母出现的次数；计数完成后，进入比较阶段，看两个字符串的计数器是否相同，如果相同则输出是变位词的结论。

# 计数比较法

def anagram_solution4(s1, s2):
    c1 = [0] * 26  # 生成一个有26个0元素的列表
    c2 = [0] * 26
    for i in range(len(s1)):
        pos = ord(s1[i]) - ord('a')  # 此字符在列表的第几位，从0开始计位
        c1[pos] += 1  # 在此计数位上+1
    for i in range(len(s2)):
        pos = ord(s2[i]) - ord('a')
        c2[pos] += 1
    return c1 == c2

print(anagram_solution4('python', 'typhon'))

计数比较算法中有3个循环迭代，但不象解法1那样存在嵌套循坏，都是单独的。前两个循环用于对字符串进行计数，操作次数等于字符串长度n，第3个循环用于计数器比较，操作次数总是26次，所以总操作次数T(n)=2n+26，其数量级为O(n)。
（计数比较性能最优，但需要更多的存储空间）

Python数据类型的性能

讨论Python中两种内置数据类型上各种操作的大O OO数量级
列表list 和字典dict

对比list 和 dict 的操作

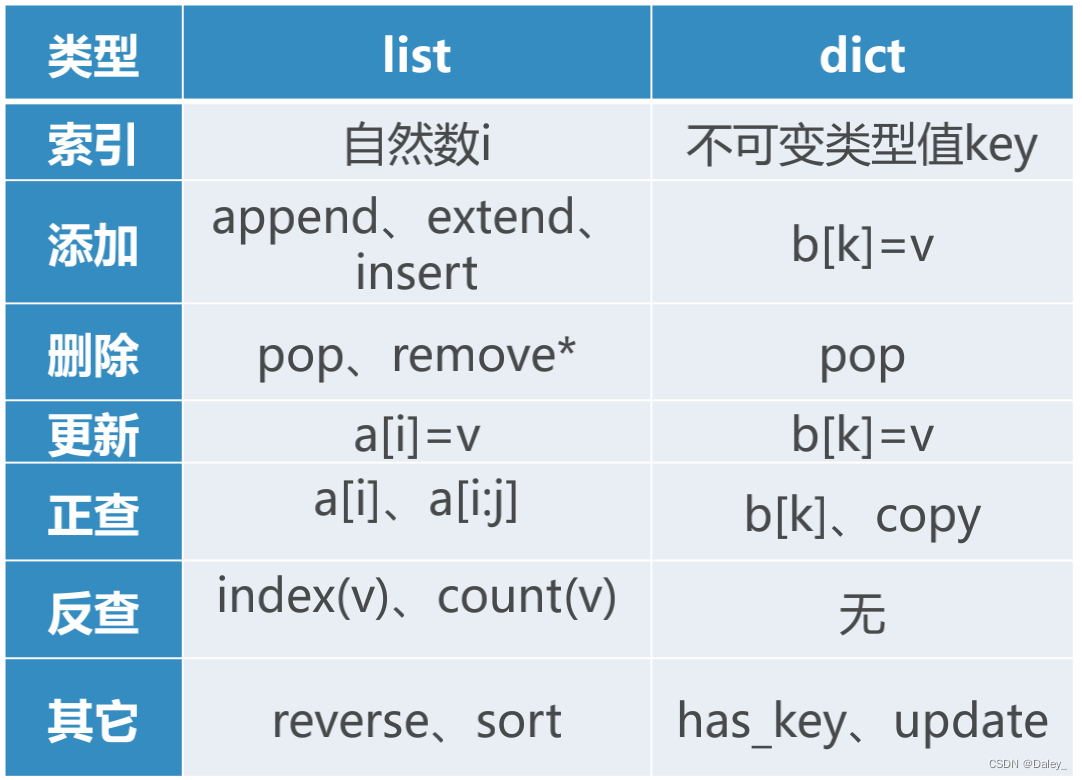
正查：根据索引查数值
反查：根据数值查索引

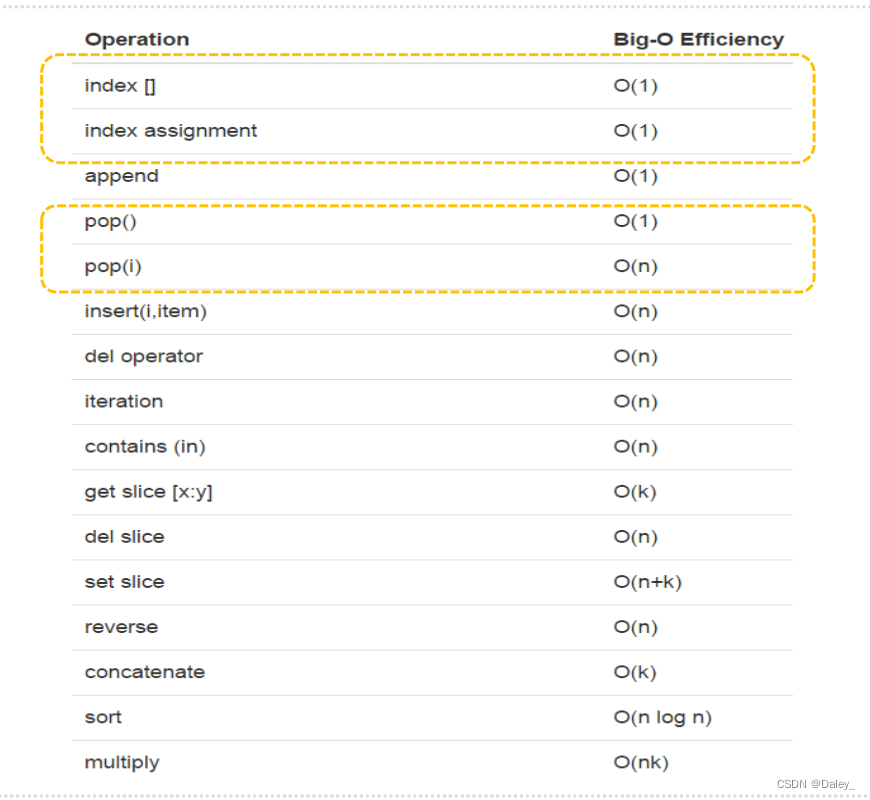
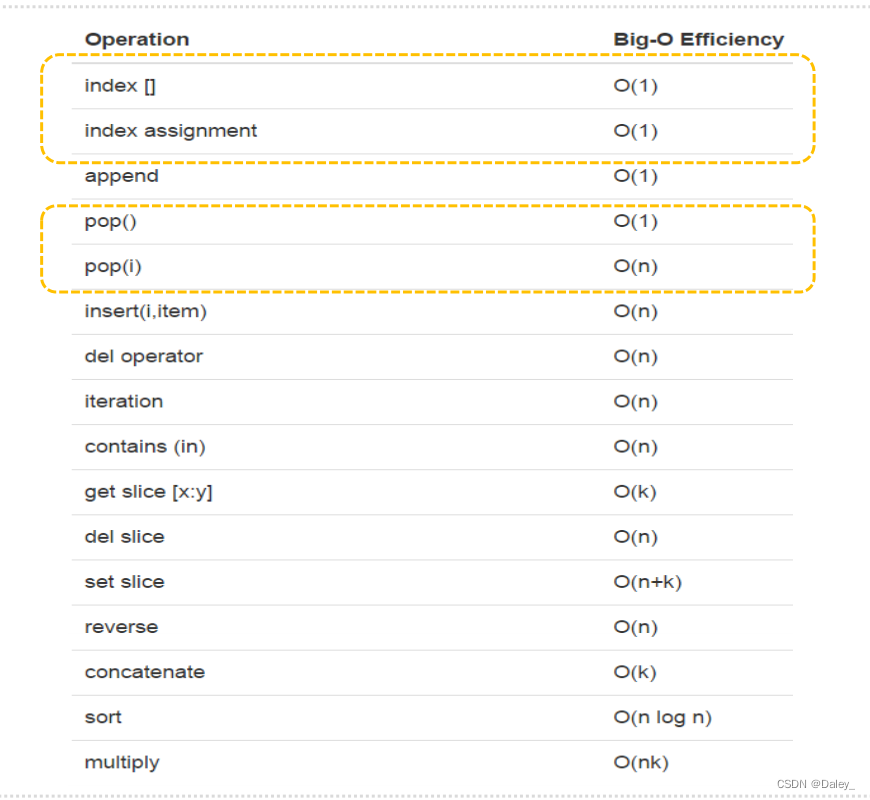
List列表数据类型常用操作性能

最常用的是：按索引取值和赋值(v=a[i], a[i]=v)
由于列表的随机访问特性，这两个操作执行时间与列表大小无关, 均为O( 1 )

另一个是列表增长，可以选择 append() 和 add()“+”
lst.append(v) , 执行时间为O ( 1 )
lst=lst + [v] , 执行时间为O ( n + k ) ，其中k是被加的列表长度

四种生成前n个整数列表的方法

1. 循环连接列表(+)方式生成

def test1():
    l = []
    for i in range(1000):
        l = l + []

2. 用append方法添加元素生成

def test2():
    l = []
    for i in range(1000):
        l.append(i)

3. 列表推导式

def test3():
    l = [i for i in range(1000)]

4. range函数调用转成列表

def test4():
    l = list(range(1000))

使用timeit模块对函数进行计时

1. 创建一个Timeit对象，指定需要反复运行的语句和只需要运行一次的“安装语句”
2. 然后调用这个对象的timeit方法，其中可以指定反复运行多少次

from timeit import Timer
t1 = Timer("test1()", "from __main__ import test1")
print("concat %f seconds\n" % t1.timeit(number=1000))  # 运行1000次

t2 = Timer("test2()", "from __main__ import test2")
print("append %f seconds\n" % t2.timeit(number=1000))

t3 = Timer("test3()", "from __main__ import test3")
print("comprehension %f seconds\n" % t3.timeit(number=1000))

t4 = Timer("test4()", "from __main__ import test4")
print("list %f seconds\n" % t4.timeit(number=1000))

运行结果

concat 1.889487 seconds

append 0.091561 seconds

comprehension 0.038418 seconds

list 0.009710 seconds

4种方法运行时间差别很大
列表连接（concat）最慢，List range最快，速度相差近200倍。append也要比concat快得多，列表推导式速度是append两倍的样子。

List基本操作的大O数量级

list.pop的计时试验

注意到：
pop()从列表末尾移除元素，O ( 1 ) 常数
pop(i)从列表中部移除元素，O ( n ) 线性

原因在于python所选择的实现方法：
从中部移除元素的话，要把移除元素后面的元素全部向前挪位复制一遍，这个看起来很笨拙，但这种实现方法能够保证列表按索引取值和赋值的操作很快，达到O ( 1 ) 。

为了验证表中的大O数量级，将两种情况下的pop操作来实际计时对比，相对同一个大小的list，分别调用pop()和pop(0)

对不同大小的list做计时，期望的结果是：
pop()的时间不随list大小变化，pop(0)的时间随着list变大而变大

import timeit
popzero = timeit.Timer("x.pop(0)", "from __main__ import x")
popend = timeit.Timer("x.pop()", "from __main__ import x")

x = list(range(2000000))
print(popzero.timeit(number=1000))
print(popend.timeit(number=1000))

# 运行结果 相差很大
1.9536310150288045
5.712697748094797e-05 # e-05 相当于除以100000 说明这个数字很小

通过改变列表的大小来测试两个操作的增长趋势

import timeit
popzero = timeit.Timer("x.pop(0)", "from __main__ import x")
popend = timeit.Timer("x.pop()", "from __main__ import x")
print("pop() pop(0)")
for i in range(1000000, 100000001, 1000000):
    x = list(range(i))
    pt = popend.timeit(number=1000)
    x = list(range(i))
    pz = popzero.timeit(number=1000)
    print("%15.5f, %15.5f" % (pt, pz)) # 15是UI定输出的字符至少是15个

运行结果

pop() pop(0)
        0.00005,         2.16132
        0.00011,         3.91013
        0.00009,         6.01475
        0.00020,         7.65026
        0.00009,        10.10475
        0.00005,        12.31715

pop()是平坦的常数
pop(0)是线性增长的趋势

dict字典类型

字典与列表不同，根据关键码（key）找到数据项，而列表是根据位置（index）
最常用的取值get和赋值set，性能为O ( 1 )
另一个重要操作contain(in) 是判断字典中是否存在某个关键码(key),性能为O ( 1 )

list和dict的in操作对比

设计一个性能试验来验证list中检索一个值，以及dict中检索一个值的计时对比
生成包含连续值的list和包含连续关键码key的dist，用随机数来检验操作符in的耗时

import timeit
import random
for i in range(10000, 1000001, 20000):
    t = timeit.Timer("random.randrange(%d) in x" % i, "from __main__ import random,x")
    x = list(range(i))
    lst_time = t.timeit(number=1000)
    x = {j: None for j in range(i)}
    d_time = t.timeit(number=1000)
    print("%d, %10.3f, %10.3f" % (i, lst_time, d_time))

运行结果

10000,      0.090,      0.001
30000,      0.164,      0.001
50000,      0.309,      0.001
70000,      0.425,      0.001
90000,      0.576,      0.001
110000,      0.652,      0.001
130000,      0.740,      0.001

可见字典的执行时间与规模无关，是常数
而列表的执行时间则随着列表的规模加大而线性上升

练习

A/B问题

题目内容：给出两个整数，输出他们的商

可以使用以下语句实现整数n的输入：n=int(input())

输入格式: 两行，每行一个整数

输出格式：输出一个数，即他们的商，保持小数点后3位（%.3f）
如果除数为0，则输出：NA（两个字母）

输入样例：
1
2

输出样例：
0.500

n=int(input())
m=int(input())
if m==0:
  print("NA")
else:
  print("%.3f" % (n/m))

打印实心矩形

题目内容：给出行数和列数，打印一个由*号构成的实心矩形。

输入格式: 一行，用空格隔开的两个整数m、n

输出格式：由*号构成的m行n列实心矩形

输入样例：
3 2

输出样例：
**
**
**

m,n = list(map(int,input().split()))
for i in range(m):
    print('*'*n)

找到最小的数

题目内容：给定若干个整数，找出这些整数中最小的，输出。

输入格式: 一行，由空格隔开的一系列整数，数量2个以上。

输出格式：最小的整数

输入样例：1 2 3 4 5 6 7 8 9 0

输出样例：0

alist = list(map(int, input().split( )))
alist.sort()
b = alist.pop(0)
# b = min(alist)
print(b)