python数据结构与算法学习之递归

递归Recursion

什么是递归

• 递归（recursion）是一种解决问题的方法，其精髓在于将问题分解为规模更小的相同问题，持续分解直到问题规模小到可以用非常简单直接的方式来解决。
• 递归的问题分解方式非常独特，其算法方面的明显特征就是在算法流程中调用自身。

递归三定律：

• 递归算法必须有一个基本结束条件（最小规模问题的直接解决）
• 递归算法必须能改变状态向基本结束条件演进（减小问题规模）
• 递归算法必须调用自身（解决减小了规模的相同问题）

递归“三定律”：数列求和问题

• 数列求和问题首先具备了基本结束条件：当列表长度为1的时候，直接输出所包含的唯一数
• 数列求和处理的数据对象是一个列表，而基本结束条件是长度为1的列表，那递归算法就要改变列表并向长度为1的状态演进我们看到其具体做法是将列表长度减少1。
• 调用自身是递归算法中最难理解的部分，实际上我们理解为“问题分解成了规模更小的相同问题”就可以了在数列求和算法中就是“更短数列的求和问题”。

# 递归版数列求和：
def listsum(numList):
    if len(numList) == 1:
        return numList[0]
    else:
        return numList[0] + listsum(numList[1:])

print(listsum([1,3,5,7,9]))

递归的应用：任意进制转换

• 假设是要转换为十进制，比十小的整数转换为十进制，直接查表就可以得到，比十大的整数就想办法拆成一系列比十小的整数，逐个查表。
• 所以递归基本结束条件就是小于十的整数，拆解整数的过程就是向基本结束条件演进的过程。
• 拆解过程分为两步：1. 除以“进制基base” （// base）；2. 对“进制基”求余数（% base）。
• 此时问题就分解为：1. 余数总小于“进制基base”，是基本结束条件，可直接查表转换；2. 整数商成为更小规模问题，通过递归调用自身解决。
  

# 递归版整数转换为任意进制：
def toStr(n,base): #  n为整数base为任意进制
    convertString = "0123456789ABCDEF"
    # print(convertString[5])
    if n < base:  
        return convertString[n]  # 最小规模
    else:
        return toStr(n//base,base) + convertString[n%base]  # 整除减小规模，调用自身

print(toStr(1453,16))

递归调用的实现：递归深度的限制

• 当一个函数被调用的时候，系统会把调用时的现场数据压入到系统调用栈。
• 每次调用，压入栈的现场数据成为栈帧，当函数返回时，要从调用栈的栈顶取得返回地址，恢复现场，弹出栈帧，按地址返回。
  
• 在Python内置的sys模块可以获取和调整最大递归深度（不然可能会出现错误：RecursionError ，因为容量有限或者未设置基本结束条件导致无限递归）

import sys
sys.getrecursionlimit()   # 返回1000
sys.setrecursionlimit(3000)
sys.getrecursionlimit()   # 返回3000

递归的可视化：分形树

• Python的海龟做图系统turtle module是Python内置的，随时可用，以LOGO语言的创意为基础，其意象为模拟海龟在沙滩上爬行而留下的足迹。

1. 爬行：forward(n); backward(n)

2. 转向：left(a); right(a)

3. 抬笔放笔：penup(); pendown()

4. 笔属性：pensize(s); pencolor©

import turtle

# 正方形：
t = turtle.Turtle()
for i in range(4):
    t.towards(100)
    t.right(90)
turtle.done()

# 五角星：
t = turtle.Turtle()
t.pencolor("red")
t.pensize(3)
for i in range(5):
    t.towards(100)
    t.right(144)
t.hideturtle()
turtle.done()

# 螺旋线：
t = turtle.Turtle()
def drawSpiral(t,lineLen):
    if lineLen > 0:
        t.forward(lineLen)
        t.right(90)
        drawSpiral(t,lineLen-5)
drawSpiral(t,200)
turtle.done()

螺旋线

• 分形树：自相似递归图形

1. 分形Fractal，是1975年由Mandelbrot开创的新学科。“一个粗糙或零碎的几何形状，可以分成数个部分，且每一部分都（至少近似地）是整体缩小后的形状”，即具有自相似的性质。
2. 分形是在不同尺度上都具有相似性的事物。

import turtle
​
def tree(branch_len):
    if branch_len > 5:   # 树干太短不画，即递归结束条件
        t.forward(branch_len)  # 画树干
        t.right(20)  # 向右倾斜
        tree(branch_len - 5)  # 递归调用，画右边的小树
        t.left(40)  # 向左回40°，向左倾斜
        tree(branch_len - 5)  # 递归调用，画左边的小树
        t.right(20)  # 向右回20°，即回正
        t.backward(branch_len)  # 海归退回原位置
        
t = turtle.Turtle()
t.left(90)
t.penup()
t.backward(100)
t.pendown()
t.pencolor('green')
t.pensize(2)
tree(75)  # 画树干长度为75的二叉树
t.hideturtle()
turtle.done()

分形树

递归的可视化：谢尔宾斯基三角形

• 分形构造，平面称谢尔宾斯基三角形，立体称谢尔宾斯基金字塔。实际上，真正的谢尔宾斯基三角形是完全不可见的，其面积为0，但周长无穷，是介于一维和二维之间的分数维（约1.585维）构造。
• 根据自相似特性，谢尔宾斯基三角形是由3个尺寸减半的谢尔宾斯基三角形按照品字形拼叠而成。由于我们无法真正做出谢尔宾斯基三角形（degree —> ∞），只能做degree有限的近似图形。
  
• 在degree有限的情况下，degree=n的三角形，是由3个degree=n-1的三角形按照品字形拼叠而成。同时，这3个degree=n-1的三角形边长均为degree=n的三角形的一半（规模减小）。当degree=0，则就是一个等边三角形，这是递归基本结束条件。

import turtle
def sierpinski(degree,points):
    colormap = ['blue','red','green','yellow','orange','pink']
    # 绘制等边三角形
    drawTriangle(points,colormap[degree])
    # 最小规模，0直接退出
    if degree > 0:
        # 减小规模，getMid边长减半，调用自身，左上右的次序
        sierpinski(degree-1,{'left':points['left'],
                            'top':getMid(points['left'],points['top']),
                            'right':getMid(points['left'],points['right'])})
        sierpinski(degree-1,{'left':getMid(points['left'],points['top']),
                            'top':points['top'],
                            'right':getMid(points['top'],points['right'])})
        sierpinski(degree-1,{'left':getMid(points['left'],points['right'])
                            'top':getMid(points['right'],points['top'])
                            'right':points['right']})
        
def drawTriangle(points,color):
    t.fillcolor(color)
    t.penup()
    t.goto(points['top'])
    t.pendown()
    t.begin_fill()
    t.goto(points['left'])
    t.goto(points['right'])
    t.goto(points['top'])
    t.end_fill()
    
def getMid(p1,p2):
    return((p1[0]+p2[0])/2,(p1[1]+p2[1])/2)
​
t = turtle.Turtle()
​
points={'left':(-200,-100),
       'top':(0,200),
       'right':(200,-100)}
​
sierpinski(5,points)
​
turtle.done()

绘制路径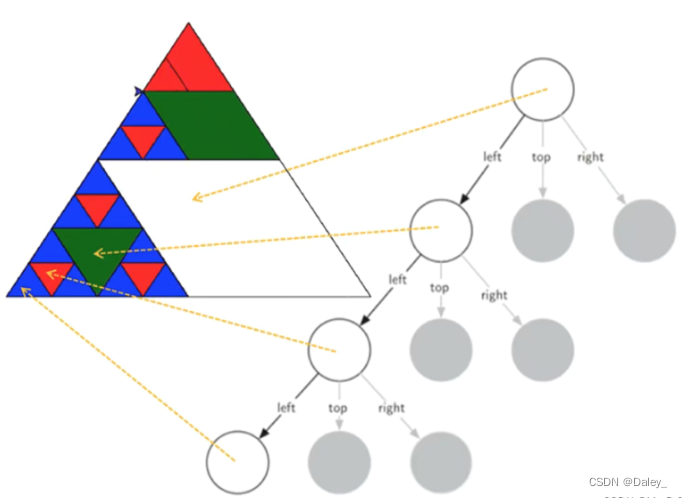

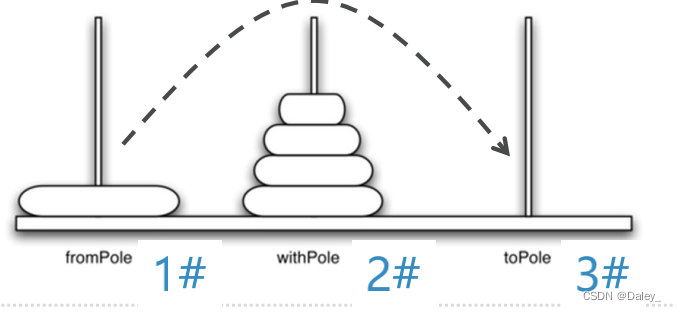
递归的应用：汉诺塔问题

递归思路：

• 将盘片塔从开始柱，经由中间柱，移动到目标柱：
  首先将上层N-1个盘片的盘片塔，从开始柱，经由目标柱，移动到中间柱；
  然后将第N个（最大的）盘片，从开始柱，移动到目标柱；
  最后将放置在中间柱的N-1个盘片的盘片塔，经由开始柱，移动到目标柱。 - 基本结束条件，也就是最小规模问题是：1个盘片的移动问题
  

# height=3
def moveTower(height,fromPole,withPole,toPole):
    if height >= 1:
        moveTower(height - 1, fromPole,toPole,withPole)
        moveDisk(height,fromPole,toPole)
        moveTower(height - 1,withPole,fromPole,toPole)

def moveDisk(disk,fromPole,toPole):
    print(f"Moving disk{disk} from{fromPole} to {toPole}")

moveTower(3,"#1","#2","#3")

递归的应用：探索迷宫

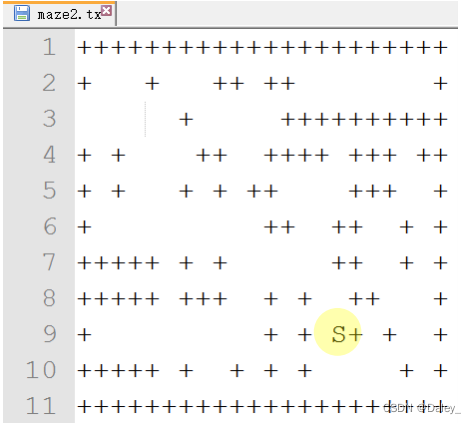
1. 迷宫的数据结构 Maze Class

• 考虑用矩阵方式来实现迷宫数据结构
  采用“数据项为字符列表的列表”这种两级列表的方式来保存方格内容
• 采用不同字符来分别代表“墙壁+”、“通道 ”、“海龟投放点S”，从一个文本文件逐行读入迷宫数据

class Maze:
    def __init__(self, mazeFileName):
        rowsInMaze = 0
        columnsInMaze = 0
        self.mazelist = []
        mazeFile = open(mazeFileName, 'r')
        rowsInMaze = 0
        for line in mazeFile:
            rowList = []
            col = 0
            for ch in line[:-1]:
                rowList.append(ch)
                if ch == 'S':
                    self.startRow = rowsInMaze
                    self.startCol = col
                col = col + 1
            rowsInMaze = rowsInMaze + 1
            self.mazelist.append(rowList)
            columnsInMaze = len(rowList)

2. 探索迷宫：算法思路

• 将海龟从原位置向北移动一步，以新位置递归调用探索迷宫寻找出口；
• 如果上面的步骤找不到出口，那么将海龟从原位置向南移动一步，以新位置递归调用探索迷宫；
• 如果向南还找不到出口，那么将海龟从原位置向西移动一步，以新位置递归调用探索迷宫；
• 如果向西还找不到出口，那么将海龟从原位置向东移动一步，以新位置递归调用探索迷宫；
• 如果上面四个方向都找不到出口，那么这个迷宫没有出口！

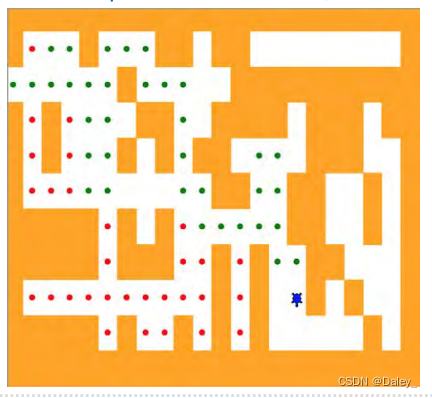
注意细节
如果我们向某个方向（如北）移动了海龟，那么如果新位置的北正好是一堵墙壁，那么在新位置上的递归调用就会让海龟向南尝试
可是新位置的南边一格，正好就是递归调用之前的原位置，这样就陷入了无限递归的死循环之中

所以需要有个机制记录海龟所走过的路径
沿途洒“面包屑”，一旦前进方向发现“面包屑”，就不能再踩上去，而必须换下一个方向尝试；
对于递归调用来说，就是某方向的方格上发现“面包屑”，就立即从递归调用返回上一级。

递归调用的“基本结束条件”归纳如下：

• 海龟碰到“墙壁”方格，递归调用结束，返回失败；
• 海龟碰到“面包屑”方格，表示此方格已访问过，递归调用结束，返回失败；
• 海龟碰到“出口”方格，即“位于边缘的通道”方格，递归调用结束，返回成功！
• 海龟在四个方向上探索都失败，递归调用结束，返回失败

# 完整代码 （cb老师讲的从96行起）
import turtle

PART_OF_PATH = 'O'
TRIED = '.'
OBSTACLE = '+'
DEAD_END = '-'

class Maze:
    def __init__(self,mazeFileName):
        rowsInMaze = 0
        columnsInMaze = 0
        self.mazelist = []
        mazeFile = open(mazeFileName,'r')
        rowsInMaze = 0
        for line in mazeFile:
            rowList = []
            col = 0
            for ch in line[:-1]:
                rowList.append(ch)
                if ch == 'S':
                    self.startRow = rowsInMaze
                    self.startCol = col
                col = col + 1
            rowsInMaze = rowsInMaze + 1
            self.mazelist.append(rowList)
            columnsInMaze = len(rowList)

        self.rowsInMaze = rowsInMaze
        self.columnsInMaze = columnsInMaze
        self.xTranslate = -columnsInMaze/2
        self.yTranslate = rowsInMaze/2
        self.t = turtle.Turtle()
        self.t.shape('turtle')
        self.wn = turtle.Screen()
        self.wn.setworldcoordinates(-(columnsInMaze-1)/2-.5,-(rowsInMaze-1)/2-.5,(columnsInMaze-1)/2+.5,(rowsInMaze-1)/2+.5)

    def drawMaze(self):
        self.t.speed(10)
        for y in range(self.rowsInMaze):
            for x in range(self.columnsInMaze):
                if self.mazelist[y][x] == OBSTACLE:
                    self.drawCenteredBox(x+self.xTranslate,-y+self.yTranslate,'orange')
        self.t.color('black')
        self.t.fillcolor('blue')

    def drawCenteredBox(self,x,y,color):
        self.t.up()
        self.t.goto(x-.5,y-.5)
        self.t.color(color)
        self.t.fillcolor(color)
        self.t.setheading(90)
        self.t.down()
        self.t.begin_fill()
        for i in range(4):
            self.t.forward(1)
            self.t.right(90)
        self.t.end_fill()

    def moveTurtle(self,x,y):
        self.t.up()
        self.t.setheading(self.t.towards(x+self.xTranslate,-y+self.yTranslate))
        self.t.goto(x+self.xTranslate,-y+self.yTranslate)

    def dropBreadcrumb(self,color):
        self.t.dot(10,color)

    def updatePosition(self,row,col,val=None):
        if val:
            self.mazelist[row][col] = val
        self.moveTurtle(col,row)

        if val == PART_OF_PATH:
            color = 'green'
        elif val == OBSTACLE:
            color = 'red'
        elif val == TRIED:
            color = 'black'
        elif val == DEAD_END:
            color = 'red'
        else:
            color = None

        if color:
            self.dropBreadcrumb(color)

    def isExit(self,row,col):
        return (row == 0 or
                row == self.rowsInMaze-1 or
                col == 0 or
                col == self.columnsInMaze-1 )

    def __getitem__(self,idx):
        return self.mazelist[idx]


def searchFrom(maze, startRow, startColumn):
  # 1.碰到墙壁，返回失败
    maze.updatePosition(startRow, startColumn)
    if maze[startRow][startColumn] == OBSTACLE :
        return False
    #  2. 碰到面包屑，或者死胡同，返回失败
    if maze[startRow][startColumn] == TRIED or maze[startRow][startColumn] == DEAD_END:
        return False
    # 3. 碰到了出口，返回成功！
    if maze.isExit(startRow,startColumn):
        maze.updatePosition(startRow, startColumn, PART_OF_PATH)
        return True
     # 4.撒一下面包屑，继续探索
    maze.updatePosition(startRow, startColumn, TRIED)
 
    # 向北南西东四个方向继续依次探索，or操作符具有短路效应，即实现一个就停止
    found = searchFrom(maze, startRow-1, startColumn) or \
            searchFrom(maze, startRow+1, startColumn) or \
            searchFrom(maze, startRow, startColumn-1) or \
            searchFrom(maze, startRow, startColumn+1)
   # 如果探索成功，标记当前点，失败则标记为“死胡同” 
    if found:
        maze.updatePosition(startRow, startColumn, PART_OF_PATH)
    else:
        maze.updatePosition(startRow, startColumn, DEAD_END)
    return found

myMaze = Maze('maze2.txt')
myMaze.drawMaze()
myMaze.updatePosition(myMaze.startRow,myMaze.startCol)

searchFrom(myMaze, myMaze.startRow, myMaze.startCol)

练习

进制转换

给定一个M进制的数，请将其转换为N进制并输出

输入格式:
两行，第一行为空格分隔的两个数字，分别为10进制表示的M与N；其中M, N均满足2 ≤ M、N ≤ 36
第二行为待转换的M进制数字，其中每位超过9的部分从10至36分别用大写字母A-Z表示；输入数据保证数据的每一位不超过M

输出格式：
一行字符串，表示转换后的N进制数

输入样例：
8 16
‭471‬

输出样例：
‭139

def toStr(numNew,N):
    coverstring = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ" # 36位
    if numNew < N:
        return coverstring[numNew]
    else:
        return toStr(numNew//N,N) + coverstring[numNew%N]

M,N = map(int,input().split(" "))
numS = input()
numNew = int(numS,M)   #将任何进制数转化为10进制数
print(toStr(numNew,N))

四柱汉诺塔

如课上所说，汉诺塔问题源于印度一个古老传说。对于原始的汉诺塔游戏，可供玩家操作的空间一共只有三根柱子，导致按原传说的要求，需要超过1.8*10^19步才能解开。
透过新增柱子可以大幅度地减少需要的步数。此处要求在给出指定的盘数，柱子数量为4（即限制为4根柱子）且不改变原有传说的其他规则的限制下，找出完成迁移的最小步骤数。

输入格式:
一个非负整数M，M代表盘数，M<=1000。

输出格式：
一个非负整数，表示完成迁移的最小步骤数。

输入样例：
3

输出样例：
5

求解此题时用到了三柱汉诺塔的次数规律，即hanoi(n) = 2^(n)-1，四柱汉诺塔可以这样理解：

1. 一共有n个盘，1，2，3，4个柱，将其中x个盘从1柱经23柱移到4柱需要f(x)步
2. 将剩下n-x个盘经2柱移到3柱为三柱汉诺塔问题，所以有2^(n-x)-1步
3. 最后再将4柱上的x个盘经12柱移到3柱上，同样需要f(x)步
4. hanoi(n) = min( 2^(n-x) - 1 + f(x)*2)) for 1<=x<=n

num = int(input())

def hanoi4(num):
    if num == 0:
        return 0
    elif n == 1:
        return 1
    elif n == 2:
        return 3
    else:
        H = []
        for x in range(1,num):
            h.append(2 * hanoi4(x) + 2 ** (num - x) - 1)          
        return min[H]
        
print(hanoi4(num))

也可以用动态规划的思想，同时存储已知的最优解

num = int(input())

def hanoi4(num):
    h_list = [0] * (n + 1)  # 初始化列表
 
    def dp(m):
        if h_list[m]:
            return h_list[m]
        result = 2 ** m - 1  # 次数最多一定不会超过三柱汉诺塔
        for x in range(1, m):
            result = min(result, 2 * dp(x) + 2 ** (m - x) - 1)
        h_list[m] = result  #记录算过的值
        return result 
        
    return dp(num)
    
print(hanoi4(num))

ASCII谢尔宾斯基地毯

谢尔宾斯基地毯是形如上图的正方形分形图案，每个地毯可分为等大小的9份，其中中央挖空，其余均由更小的地毯组成。
现给定地毯大小（行数）与组成地毯的字符元素，请打印相应的地毯图形。
注：空腔以半角空格表示；当给定字符元素长度不为1时空格数须与字符长度对应

输入格式:
输入为两行，分别为地毯大小正整数N与组成元素字符串c
输入数据保证N为3的正整数幂

输出格式：
由N行长度为N*len©的字符串构成的谢尔宾斯基地毯

输入样例：
9
[]

输出样例：

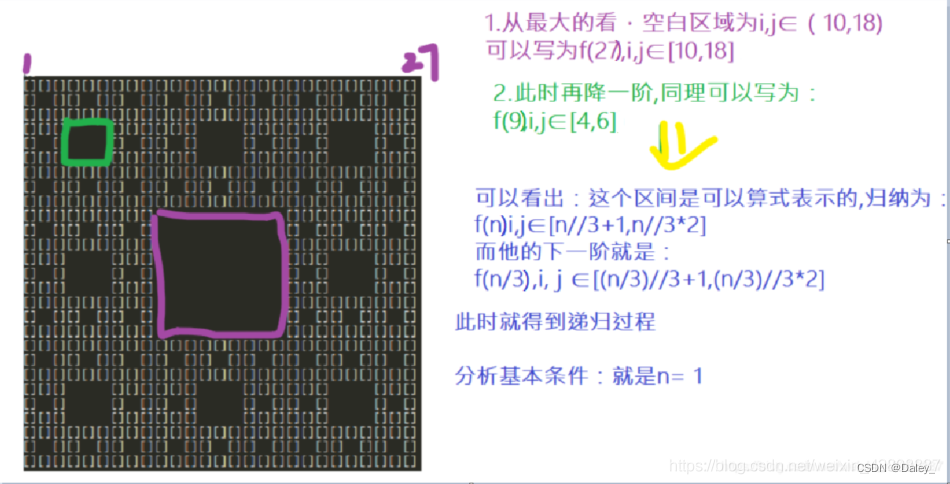
(图片思路from 加油啊DuXY)

def carpet(N,char):
    def checkblank(n,i,j):
        if n <= 1:
            return True
        n2 = n/3
        if n2 < i <= n2 * 2 and n2 < j <= n2 * 2:
            return False
        return checkblank(n2,i%n2,j%n2)
    
    
    for i in range(1,N+1):
        for j in range(1,N+1):
            if checkblank(N,i,j):
                print(char,end = "")
            else:
                print(" "*len(char),end = "")
        print('')
 
n=int(input())
c=input()
carpet(n,c)

分治策略

分治策略：分而治之，将问题分为若干更小规模的部分，通过解决每一个小规模部分问题，并将结果汇总得到原问题的解。

优化问题和贪心策略

找零兑换问题的递归解法

1. 找零兑换问题
   假设为自动售货机厂家编写程序，自动售货机每次要找给顾客数量最少的硬币。

贪心策略Greedy Method：每次都试图解决问题尽量大的一部分。
贪心策略解法：从最大面值的硬币开始，用尽量多的数量，有余额的，再到下一最大面值的硬币，还用尽量多的数量，一直到最小面值硬币为止。

注意：贪心策略依赖币值的分布，如果币值设置特殊，则贪心策略就会实效。

2. 递归解法：

• 兑换硬币最简单直接的情况就是需要兑换的面值正好等于某种硬币，就只用找零1枚硬币，也就是递归的基本结束条件。
• 其次需要减小问题的规模，我们要对每种硬币尝试1次，例如美元体系：找零减去1分(penny)后，求兑换硬币最少数量(递归调用自身)；找零减去5分(nikel)后，求兑换硬币最少数量；找零减去10分(dime)后，求兑换硬币最少数量；找零减去25分(quarter)后，求兑换硬币最少数量；上述4项中选择最小的一个。

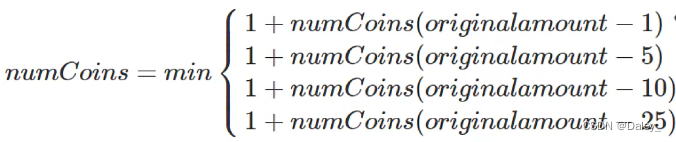
# 效率极差递归解法：
def recMC(coinValueList,change):
    minCoins = change
    if change in coinValueList:  # 最小规模，直接返回，正好等于硬币面值
        return 1
    else:
        for i in [c for c in coinValueList if c <= change]: # 选比要找零面值小的硬币
            numCoins = 1 + recMC(coinValueList,change-i) 
                                      #调用自身减小规模
            if numCoins < minCoins:
                minCoins = numCoins
    return minCoins
print(recMC([1,5,10,25],63))

上述代码效率低下的重要原因就是重复计算太多，算法改进的关键就在于消除重复计算。可以用一个表将计算过的中间结果保存起来，在计算之前查表看看是否已经计算过。这个算法的中间结果就是部分找零的最优解，在递归调用过程中已经得到的最优解被记录下来。在递归调用之前，先查找表中是否已有部分找零的最优解，如果有，直接返回最优解而不进行递归调用，如果没有才进行递归调用。

# 递归解法改进代码： 极大减少了递归调用的次数
def recDC(coinValueList,change,knownResults):
    minCoins = change
    if change in coinValueList:  # 递归基本结束条件
        knownResults[change] = 1 # 记录最优解
        return 1
    elif knownResults[change] > 0:
        return knownResults[change] # 查表成功，直接用最优解
    else:
        for i in [c for c in coinValueList if c <= change]:
            numCoins = 1 + recDC(coinValueList,change-i,knownResults)
            if numCoins < minCoins:
                minCoins = numCoins
                # 找到最优解，记录到表中
                knownResults[change] = minCoins
    return minCoins

print(recDC([1,5,10,25],63,[0]*64))

中间结果记录可以很好的解决找零兑换问题。实际上，这种方法还不能称为动态规划，而是叫做”memoization（记忆化/函数值缓存）“的技术提高了递归解法的性能。

找零兑换的动态规划解法

• 从最简单的“1分钱找零”的最优解开始，逐步递加上去，直到我们需要的找零钱数。
• 在找零递加的过程中，设法保持每一分钱的递加都是最优解，一直加到求解找零钱数，自然得到最优解。
• 问题的最优解包含了更小规模子问题的最优解，这是一个最优化问题能够用动态规划策略解决的必要条件。

具体例子：采用动态规划来解决11分钱的兑换问题：

1. 从1分钱兑换开始，逐步建立一个兑换表
   
2. 计算11分钱的兑换法，我们做如下几步：
   首先减去1分硬币，剩下10分钱查表最优解是1（2个）
   然后减去5分硬币，剩下6分钱查表最优解是2（3个）
   最后减去10分硬币，剩下1分钱查表最优解是1（2个）
3. 通过上述最小值得到最优解：2个硬币

def dpMakeChange(coinValueList,change,minCoins):
    # 从1分开始到change逐个计算最少硬币数
    for cents in range(1,change+1):
        # 1. 初始化一个最大值
        coinCount = cents
        # 2. 减去每个硬币，向后查最少硬币数，同时记录总的最少数
        for j in [c for c in coinValueList if c <= cents]:
            if minCoins[cents - j] + 1 < coinCount:
                coinCount = minCoins[cents - j] + 1
        # 得到当前最少硬币数，记录在表中
        minCoins[cents] = coinCount
    # 返回最后一个结果
    return minCoins[change]

print(dpMakeChange([1,5,10,21,25],63,[0]*64))

动态规划中最主要的思想是：

• 从最简单情况开始到达所需找零的循环
• 其每一步都依靠以前的最优解来得到本步骤的最优解，直到得到答案。

动态规划算法的扩展：前面的算法已经得到了最少硬币的数量，但没有返回硬币如何组合。扩展算法的思路很简单，只需要在生成最优解列表的同时跟踪记录所选择的那个硬币币值即可。在得到最后的解后，减去选择的硬币币值，回溯到表格之前的部分找零，就能逐步得到每一步所选择的硬币币值。

# 代码改进：返回硬币如何组合
def dpMakeChange(coinValueList,change,minCoins,coinsUsed):
    for cents in range(1,change+1):
        coinCount = cents
        newCoin = 1  # 初始化一下新加硬币
        for j in [c for c in coinValueList if c <= cents]:
            if minCoins[cents - j] + 1 < coinCount:
                coinCount = minCoins[cents - j] + 1
                newCoin = j  # 对应最小数量，所减的硬币
        minCoins[cents] = coinCount
        coinsUsed[cents] = newCoin   # 记录本步骤加的1个硬币
    return minCoins[change]

def printCoins(coinsUsed,change):
    coin = change
    while coin > 0:
        thisCoin = coinsUsed[coin]
        print(thisCoin)
        coin = coin - thisCoin

amnt = 63
clist = [1,5,10,21,25]
coinsUsed = [0]*(amnt+1)
coinCount = [0]*(amnt+1)

print("Making change for",amnt,"requires")
print(dpMakeChange(clist,amnt,coinCount,coinsUsed),"coins")
print("They are:")
printCoins(coinsUsed,amnt)
print("The used list is as follows:")
print(coinsUsed)

动态规划案例：博物馆大盗

大盗潜入博物馆，面前有5件宝物，分别有重量和价值，大盗的背包仅能负重20公斤，请问如何选择宝物，总价值最高？

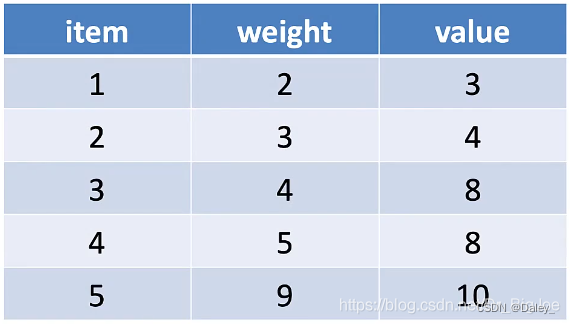
思路：

• 我们把m(i, W)记为：前i(1 <= i <= 5)个宝物中，组合不超过W(1 <= W <= 20)重量，得到的最大价值m(i, W)应该是m(i-1, W)和m(i-1, W-Wi)+vi两者最大值。我们从m(1, 1)开始计算到m(5, 20)。
  
  
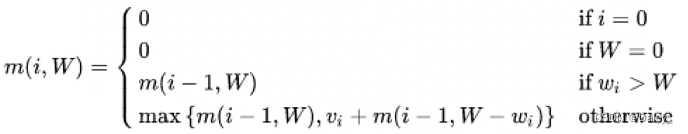
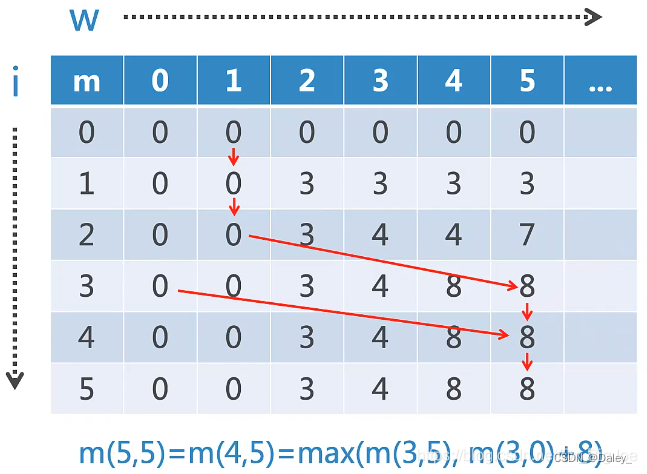
  从图表中我们可以知道：m(5,5)=m(4,5)=max(m(3,5), m(3,0)+8)

动态规划代码实现：

# 宝物的重量和价值
tr = [None,{'w':2,'v':3},{'w':3,'v':4},{'w':4,'v':8},
      {'w':5,'v':8},{'w':9,'v':10}]
max_w = 20  # 大盗最大承重
# 初始化二维表格m[(i,w)]，表示前i个宝物中，最大重量w的组合，所得到的最大价值
# 当i什么都不取，或w上限为0，价值均为0
m = {(i,w):0 for i in range(len(tr))
                for w in range(max_w+1)}
# 逐个填写二维表格
for i in range(1,len(tr)):
    for w in range(1,max_w+1):
        if tr[i]['w'] > w:  # 装不下第i个宝物
            m[(i,w)] = m[(i-1,w)]  # 不装第i个宝物
        else:
            # 不装第i个宝物，装第i个宝物，两种情况下最大价值
            m[(i,w)] = max(
                m[(i-1,w)],
                m[(i-1,w-tr[i]['w'])] + tr[i]['v'])
print(m[(len(tr)-1,max_w)])

递归代码实现：

# 宝物的重量和价值
tr = {(2,3),(3,4),(4,8),(5,8),(9,10)}
max_w = 20  # 大盗最大承重

m = {} # 初始化记忆化表格m，key是(宝物组合,最大重量)，value是最大价值

def thief(tr,w):
    if tr == set() or w == 0:
        m[(tuple(tr),w)] = 0
        return 0
    elif (tuple(tr),w) in m:  # 若该组合已经存在与记忆化表格m，就直接返回
        return m[(tuple(tr),w)]
    else:
        vmax = 0
        for t in tr:
            if t[0] <= w:
                # 逐个从集合中去掉某个宝物，递归调用
                # 选出所有价值中的最大值
                v = thief(tr-{t},w-t[0]+t[1])
                vmax = max(vmax,v)
        m[(tuple(tr),w)] = vmax
        return vmax

print(thief(tr,max_w))

小结

• 递归是解决某些具有自相似的复杂问题的有效技术。
• 递归算法“三定律”：

（1）具备基本结束条件

（2）减小规模、改变状态、向基本结束条件演进

（3）递归必须调用自身

• 如果没有缩小规模会使得调用栈溢出，使得递归失败。
• 某些情况下，递归可以代替迭代循环。
• 递归算法通常能够跟问题的表达自然契合。
• 递归不总是最合适的算法，有时候递归算法会引发巨量的重复计算。
• “记忆化/函数值缓存”可以通过附加存储空间中间计算结果来有效减少重复计算。
• 如果一个问题最优解包括规模更小相同问题的最优解，就可以用动态规划来解决。

练习

铺瓷砖

给定一个长度为N的区域，及4种不同长度的瓷砖：灰瓷砖（长为1格）、红瓷砖（长为2格）、绿瓷砖（长为3格）与蓝瓷砖（长为4格），求所有不同的铺满整个区域的方法数。

例如：当N=5时，共有15种铺满区域的方法，示意图如下：

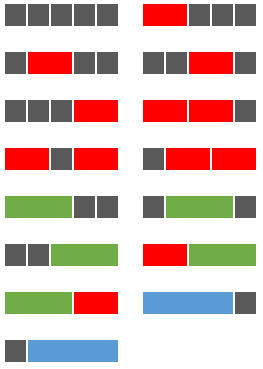
输入格式:
一个自然数N

输出格式：
一行数字，表示不同的方法总数

输入样例：
5

输出样例：
15

时间限制：500ms内存限制：32000kb

长度为N的区域，铺装方法total(N)=
第一块铺灰（1），total(N-1)
+第一块铺红（2），total(N-2)
+第一块铺绿（3），total(N-3)
+第一块铺蓝（4），total(N-4)

# 递归方法
n = int(input())
cache = {0:1,1:1,2:2,3:4,4:8}

def total(n):
    if n <= 4:
        return cache[n]
    elif n in cache:
        return cache[n]
    else:
       cache[n] = total(n-1)+total(n-2)+total(n-3)+total(n-4)
       return cache[n]

分发糖果

老师想给孩子们分发糖果，有 N 个孩子站成了一条直线，老师会根据每个孩子的表现，预先给他们评分。

你需要按照以下要求，帮助老师给这些孩子分发糖果：
每个孩子至少分配到 1 个糖果。
相邻的孩子中，评分高的孩子必须获得更多的糖果。
那么这样下来，老师至少需要准备多少颗糖果呢？

输入格式:
一个列表，以文本格式的有效Python表达式给出

输出格式：
一行数字，表示满足分配条件所需的最少糖果数

输入样例：
[1,2,2]

输出样例：
4
注：可行的分配方案为1、2、1 颗糖果；第三个孩子只得到1颗糖果也满足题目条件

贪心策略思路：

• 记录评分ratings，和对应的糖果数cds
• 将小朋友的评分按照次序加入
  第一个，无论多少分，只有一颗糖果；
  后续的：
  如果分数高于前一个，则比前一个多一颗糖果；
  如果分数与前一个相同，则给最低标准一颗；
  如果分数低于前一个，则给最低标准一颗；
  但是，如果前一个仅有一颗糖果，就需要加一颗糖果，并向前继续加，直到评分不递增，或者糖果有多。

def candy(ratings):
    cds = [1] * len(ratings) # 糖果列表

    for i in range(1,len(ratings)):
        if ratings[i -1] < ratings[i]:
            cds[i] = cds[i-1] + 1 # 分数高，比前面一个多一颗糖
        elif ratings[i-1] == ratings[i]:
            cds[i] = 1 #分数相同，给最低标准一颗
        else:
            cds[i] = 1 # 分数低，给最低标准一颗
            if cds[i-1] == 1: #但如果前面仅有一颗糖，需要加糖
                for k in range(i-1,-1,-1):
                    cds[k] += 1
                    #评分向前递增，糖果数没有递增，需要加糖
                    if k>0 and (ratings[k] >= ratings[k-1] \
                               or cds[k] < cds[k-1]):
                         break
    return sum(cds)

表达式按不同顺序求值

给定一个表达式字符串，求出按不同的求值顺序可能得到的所有结果

输入格式:
一行字符串，仅包含0-9与运算符+、-与*
注：字符串保证三种运算符左右均为数字字符

输出格式：
所有不重复的可能的结果，从小到大排序并以半角逗号","分隔

输入样例：
23-45

输出样例：
-34,-14,-10,10

注：
(2*(3-(45))) = -34
((23)-(45)) = -14
((2(3-4))5) = -10
(2((3-4)5)) = -10
(((23)-4)*5) = 10

思路：
对nums,ops的运算次序组合进行穷举
nums:剩余操作数列表
ops：剩余运算符列表

def findWays(expr):
    # 用于将字符串转为数字与运算符，供参考
    nums, ops = [], []
    num = 0
    for c in expr:
        if '0' <= c <= '9':
            num = num * 10 + ord(c) - 48
        else:
            ops.append(c)
            nums.append(num)
            num = 0
    else:
        nums.append(num)
    results = set()
    
# 头两个数入栈，头一个运算符入栈，递归调用
calc(nums[2:],ops[1:],[nums[0],nums[1]],[ops[0]])
# 结果排序 输出
ret = sorted(list(results))
return ",".join(map(str,ret))